计算机控制技术——温控系统大林算法控制器设计实验

1. 一、实验目的与要求： （1） 掌握大林控制算法原理； （2） 自行开发大林控制算法工程并实验，加深对大林算法的理解； （3） 测试并分析各种不同参数对控制效果的影响； （4） 基于大林控制算法，完成温度控制系统的仿真分析和实时控制研究。

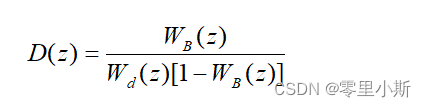
   二、实验原理： 大林算法控制目标是：设计合适的数字控制器，使整个闭环系统的传递函数为带有纯滞后的一阶惯性环节，且要求闭环系统的纯滞后时间等于对象的纯滞后时间，即：                            (4.12) 考虑到零阶保持器的作用，整个系统的闭环脉冲传递函数可由下式导出：                       (4.13) 被控对象数学模型为一阶惯性环节：                           (4.14) 其广义对象的脉冲传递函数为：                       (4.15) 根据闭环传递函数推导出数字控制器的脉冲传递函数5                        (4.16) 按照上式设计数字控制器即可实现大林控制算法控制。

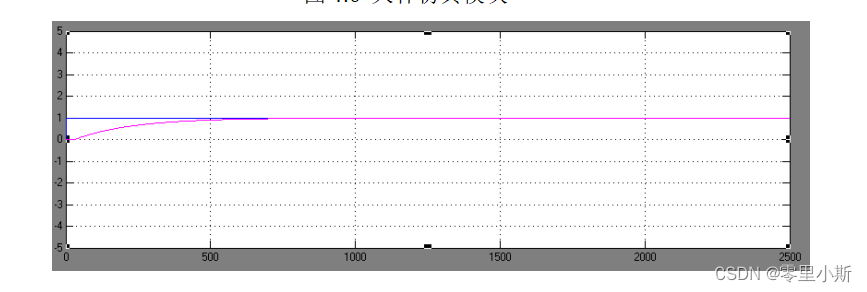
   三、实验过程及内容： 首先使用Simulink搭建大林算法控制模型，具体模型（图4.6）所示：可以得到图4.7所示的仿真曲线，通过曲线我们可以看到温度无超调。 图4.6 大林仿真模块 图4.7 仿真曲线 打开KEIL软件建立工程，名为温度大林，大林控制算法核心代码如图4.8，编写好的大林算法代码后经过编译无误后将该工程下的wd.hex文件下载到目标板中，通过上位机观察实际的控制曲线，控制曲线如4.9所示，发现温度明显无超调（默认设定值35度）。但是稳态值存在一定的误差。需进一步的进行功能化改进。 int DL_Control(float reftemp,float realtemp) {  int duty_err;      SetTemp = reftemp;  ActualTemp = realtemp;      err = SetTemp-ActualTemp;  duty_err = 0.99898 * ux[0] + 0.0049875 * ux[30] + 30.56 * err - 30.53 * err_next;  err_last = err_next;      err_next = err;  for(i = 34; i > 0; i--)  {   ux[i] = ux[i - 1];      }      ux[i] = duty_err;    if(duty_err > 250)  { duty_err = 255;      }  if(duty_err < 0)  { duty_err = 0;  }      return duty_err; } 图4.8  大林算法核心代码 图4.9  实际控制曲线 四、实验结果： 本次实验所用温度模块的传递函数为： 根据计算可得数字控制器的脉冲传递函数为： 建模系统如下： 仿真结果曲线如下：

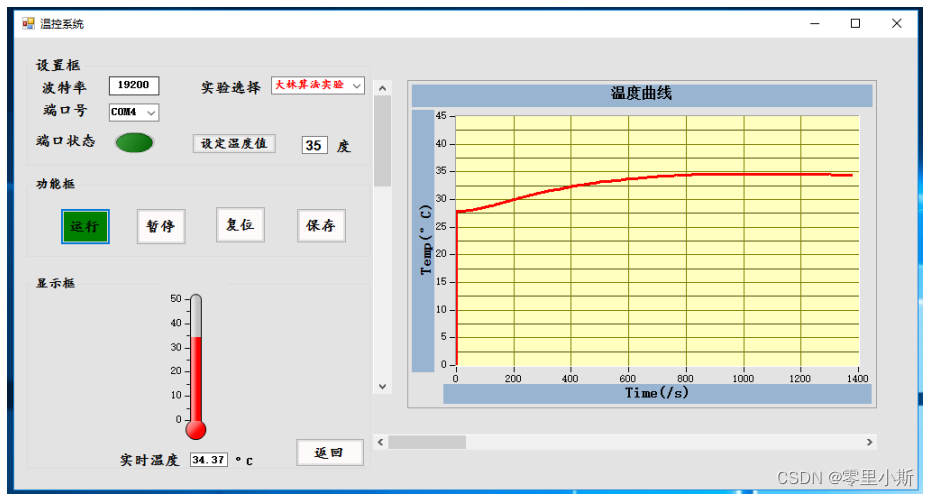
   实际运行曲线如下： 控制效果分析：通过仿真曲线和实际曲线可以看出，大林控制算法有着很高的响应速度并且稳定性也非常不错。另外大林控制算法还能实现实时自适应性控制。

   五、实验总结与思考题 思考题 什么是大林控制算法？ 大林控制算法 (DLM: Dynamic Linear Models) 是一种基于线性状态空间模型的统计方法，用于对随时间变化的数据进行建模和预测。它将观测值分解为由高度结构化的系统和关系决定的状态序列和与状态相关的观测噪声。 在该模型中，状态变量描述了系统真实的未知状态，并且通过时间变化而发生。 大林控制应用在什么控制环境下？ a.反应堆保护系统 b.电力系统  c.航天与飞行器系统 d.医疗设备医疗设备 （3）闭环传递函数的时间常数对控制效果有怎样的影响，为什么？ 影响：当时间常数较小时，闭环系统的响应速度较快可以更加迅速地对输入发生变化做出响应，在动态性能和稳态误差方面表现优异。因此，在采用大林算法进行控制设计时，通常会将时间常数设置得尽可能小。另一方面，当时间常数较大时，闭环系统的响应速度较慢，系统的动态性能会受到影响，但同时也可以帮助减少稳态误差。 原因：这是因为时间常数反映了闭环系统中信号传输的速度，即系统在对输入发生变化时的响应速度。