mean-pooling（平均池化），max-pooling（最大池化）、Stochastic-pooling（随机池化）和global average pooling（全局平均池化）的区别简介

    在神经网络中，我们经常会看到池化层，常用的池化操作有四种：mean-pooling（平均池化），max-pooling（最大池化）、Stochastic-pooling（随机池化）和global average pooling（全局平均池化），池化层有一个很明显的作用：减少特征图大小，也就是可以减少计算量和所需显存。

    mean-pooling（平均池化）：即对邻域内特征点只求平均

    优缺点：能很好的保留背景，但容易使得图片变模糊

    正向传播：邻域内取平均

 反向传播：特征值根据领域大小被平均，然后传给每个索引位置

 

   max-pooling（最大池化）：即对邻域内特征点取最大

    优缺点：能很好的保留纹理特征，一般现在都用max-pooling而很少用mean-pooling

    正向传播：取邻域内最大，并记住最大值的索引位置，以方便反向传播

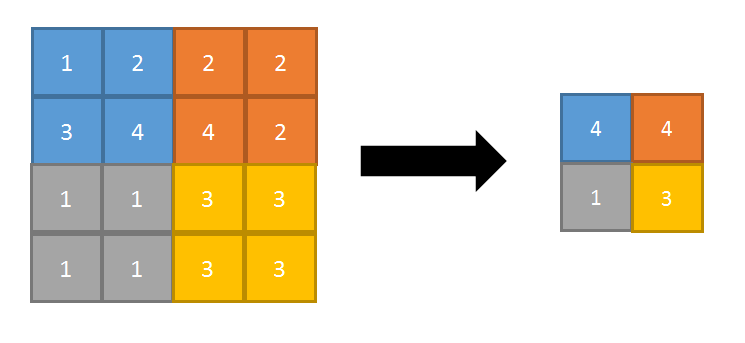
反向传播：将特征值填充到正向传播中，值最大的索引位置，其他位置补0

 

   

Stochastic-pooling（随机池化）：只需对feature map中的元素按照其概率值大小随机选择，即元素值大的被选中的概率也大。而不像max-pooling那样，永远只取那个最大值元素。

    在区域内，将左图的数值进行归一化处理，即 1/（1+2+3+4）=0.1；2/10=0.2；3/10=0.3；4/10=0.4
 

     接着按照概率值来随机选择，一般情况概率大的，容易被选择到，比如选择到了概率值为0.3的时候，那么（1，2，3，4）池化之后的值为3。使用stochastic pooling时(即test过程)，其推理过程也很简单，对矩阵区域求加权平均即可，比如上面图中，池化输出值为：1*0.1+2*0.2+3*0.3+4*0.4=3。在反向传播求导时，只需保留前向传播已经记录被选中节点的位置的值，其它值都为0,这和max-pooling的反向传播非常类似，具体可以参见上面的max-pooling反向传播原理。

    优点：方法简单，泛化能力更强（带有随机性）

 

    global average pooling（全局平均池化）：全局平均池化一般是用来替换全连接层。在分类网络中，全连接层几乎成了标配，在最后几层，feature maps会被reshape成向量，接着对这个向量做乘法，最终降低其维度，然后输入到softmax层中得到对应的每个类别的得分，过多的全连接层，不仅会使得网络参数变多，也会产生过拟合现象，针对过拟合现象，全连接层一般会搭配dropout操作。而全局平均池化则直接把整幅feature maps（它的个数等于类别个数）进行平均池化，然后输入到softmax层中得到对应的每个类别的得分。在反向传播求导时，它的参数更新和mean-pooling（平均池化）很类似，可以参考上面的内容。

    优点：大幅度减少网络参数（对于分类网络，全连接的参数占了很大比列），同时理所当然的减少了过拟合现象。赋予了输出feature maps的每个通道类别意义，剔除了全连接黑箱操作。