零基础学控制

前言

2023年7月11日，给同事做了一次控制基础的培训（其实就是最基础知识的分享），之前花了一些时间学习控制知识，觉得自己稍微了解了一些基础，决定不停下来，通过持续更新这个博客，把控制的基础知识做一个梳理和全景的学习。

网络上优秀的学习资料浩如烟海，我写的肯定是比较差的，但是，因为我是小白零基础，所以写的东西可能也适合小白零基础。与志同道合者一块努力吧！

控制在机电设备开发里是必须要掌握的，不论哪个领域都是，这一点不要侥幸，你是软件，硬件，测试，开发，甚至项目管理，在设备领域做，控制肯定要懂一点才好。对于其他工科领域，控制也无处不在，学学没坏处。

中文伟大，“控制”这个词本身有太多的意思，而这里，主要指的是反馈控制为基础的自动控制，姐妹兄弟我们开始吧。（2023年7月12日早）

更新备注

2023年7月12日早 初稿：完成前言和章节列表

2023年7月13日早 1更：从频率响应法开始写（5.1.1）

2023年7月14日早 2更：开始伯德图小节（5.2）

2023年7月15日早 3更：伯德图（5.2）

2023年7月16日早 4更：伯德图（5.2）+ 奈奎斯稳定判据（5.5）

2023年7月20日早 5更：奈奎斯稳定判据（5.5）

2023年7月26日晚 6更：根轨迹法

2023年7月30日早 7更：根轨迹法

参考文献与资源

1. 现代控制工程 第五版 Katsuhiko Ogata 著
2. 控制之美[卷一] 王天威 著
3. 自动控制原理（第二版）王建辉 顾树生 编（本书只涉及经典控制）
4. https://python-control.readthedocs.io/en/0.9.4/ 
5. https://fbswiki.org/wiki/index.php/Main_Page

第1章：基本概念

第2章：动态系统建模

第3章：时域分析

第4章：根轨迹法

4.1引言

        线性系统的稳定性完全由它的特征根（闭环极点）决定。系统的品质则取决于闭环极点和零点，根轨迹法就是用开环传递函数求闭环特征根。它是一种用图解方法表示特征根与系统参数的全部数值关系的方法（有时单靠调整增益可以将闭环极点移动到需要的位置，但不到满意的结果的话，增加校正器来解决）。根轨迹法，是一种用图解的方法标着特征根（闭环极点）与系统的某个参数全部的数值关系（通常是开环增益，但是其他参数也是可以的）。当改变增益值或者增加开环极点或/和零点时，设计者可以根据根轨迹法预测对闭环极点的位置的影响。设计系统时，根轨迹法指出了开环极点和零点应当怎样变化，才能使得响应满足系统的性能指标。

        

第5章：频率响应法

5.1 引言

• 系统对正弦信号的稳定响应称为频率响应。频率响应法做系统分析获得的信息与根轨迹法获得的信息不同，可以说两种方法互为补充，控制工程人员必须熟悉两种方法。
• 频率响应法的优点是：

1. 可以利用对物理系统测量得到的数据，而不必推导系统的数学模型。
2. 采用正弦信号发生器和精密测量装置，完成频率响应试验比较简单且精确。
3. 一些复杂元器件的传递函数也可以通过频率响应试验予以确定
4. 可以设计出一种抗噪声干扰的系统（滤波？），不希望的噪声可以忽略不计
5. 可以推广到某些非线性系统

• 奈奎斯特稳定判据，使我们有可能根据系统的开环频率响应特性信息，研究闭环系统的绝对稳定性和相对稳定性。
• 注意：控制系统的频率响应提供了瞬态响应的定性描述，但是除了二阶系统，频率响应与瞬态响应的关系是间接的。

5.1.1系统对正弦信号的稳态输出

• 系统的稳态输出可以直接从正弦传递函数得到。
• 正弦传递函数：用jw代替传递函数中的s得到的函数，w为角频率。
• 对于稳定线性定常系统，如果输入量为正弦信号，稳态输出也是一个相同频率的正弦信号，只是振幅和相角有可能不同。

图5.1 标稳定线性定常系统题

• 如图5.1的系统，假设输入为 x(t)=Xsinwt，它的拉氏变换为公式5.1，考虑G(s)代表的系统是稳定线性定常的（稳态响应与与初始条件无关），则Y(s)有以下两种情况：
  1. 具有不同的极点（相异极点型）
  2. 包含重极点（多重极点型）

公式5.1：幅值为X的正弦函数的拉氏变换

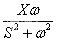
• 无论是情况1（公式5.2）还是情况2（公式5.3），y(t)在t趋向无穷大时，除了输入的正弦波带来的前两项，其他都会趋于零。

公式5.2：相异极点型系统对正弦输入的s域输出

公式5.3：含有1组多重极点的系统对于正弦输入的s域输出（注意最后一项）

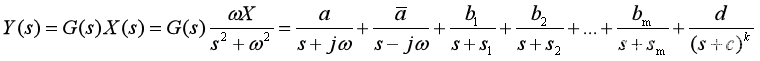
• 最后的稳态输出：

公式5.4：系统的时域稳态输出

• 经过推导进一步可以得到：

公式5.5：输出与输入同频率，相差一个相位（输出与输入的相位差）

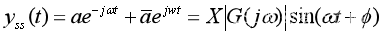
• 相位差（输出-输入）为正，叫相位超前，否则为相位滞后。
• 正弦传递函数作为频率w的复变函数，可以以频率作为参量，用其幅值和相角来描述。以下是三类正弦传递函数的图形表示法：

1. 伯德图（对数坐标）
2. 奈奎斯特图（极坐标）
3. 尼科尔斯图（对数幅相图）

5.2 伯德图

• 伯德图的组成
  1. 正弦传递函数幅值的半对数坐标图（幅频特性图）
  2. 正弦传递函数相角的半对数坐标图（相频特性图）
• 伯德图的优点
  1. 幅值相乘转化为相加
  2. 建立在渐近线基础上的简便快速绘图
  3. 可以通过实验确定传递函数
• 任意正弦传递函数的基本因子（）
  1. 增益K
  2. 积分和微分因子
  3. 一阶因子
  4. 二阶因子

• 熟悉了上面的因子的半对数坐标图后，就可以对各个单独曲线一一相加，获得任意正弦传递函数的合成半对数坐标图。

• 谐振频率和谐振峰

  二阶因子的幅值为其中 为最小值时，达到峰值，设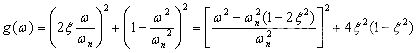可以看到即的时候为最小值，此时的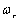为谐振频率。注意为系统的阻尼自然频率。比较谐振频率，可以有如下结论：
  1. 到阻尼比趋近与零时，谐振频率，和阻尼自然频率都趋近与无阻尼自然频率
  2. 在时，谐振频率小于阻尼自然频率
  3. 当时，不产生谐振峰值，幅值随着频率增大而单调减小。
• 最小相位系统和非最小相位系统
  1. 在s右半平面既无极点又无零点的传递函数，称为最小相位传递函数。
  2. 在具有相同的幅值特性的系统中，最小相位传递函数的相角范围是所有系统里最小的。
  3. 最小相位系统，传递函数有单一的幅值曲线确定，非最小相位系统，则不是（注意，全通滤波器乘以传递函数，不会改变幅值曲线，但会改变相位曲线）

5.3 奈奎斯特图（极坐标）

5.4 尼科尔斯图（对数幅相图）

5.5 奈奎斯稳定判据

• 奈奎斯稳定判据：根据开环频率响应和开环极点，无须求出闭环极点，就可以确定闭环系统的稳定性。
• 考虑如下的闭环系统：

        特征方程是： ，闭环系统稳定的前提是特征方程全部的根都要位于s左半平面（开环传递函数的零点和极点可能位于右半平面）。

第6章：PID控制器

第7章：非线性系统

第8章：线性离散系统

第9章：状态空间分析

第10章：状态空间设计

第11章：新时代的控制方法概览