LeNet-5网络 CIFAR10数据集分类任务

FeSCN6

于 2024-06-14 18:46:23 发布

阅读量991

点赞数 30

文章标签：分类计算机视觉

本文链接：https://blog.csdn.net/m0_62042674/article/details/139688131

版权

1. 构建LeNet-5网络，在CIFAR10数据集上完成分类任务：

（1）构建LeNet-5网络

LeNet-5网络由两个卷积层、两个池化层和三个全连接层构成。选择使用最大池化，激活函数设置为需要传入的参数，便于完成实验2的对比。前向传播过程为：1）第一层卷积 -> 激活函数 -> 第一层池化；2）第二层卷积 -> 激活函数 -> 第二层池化；3）三个全连接层。

网络搭建代码如下：

class LetNet5(nn.Module):  
    def __init__(self, activation):  
        super(LetNet5, self).__init__()  
        # 激活函数  
        self. activation = activation  
        # 第一层卷积  
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=6, kernel_size=5)  
        # 第一层池化  
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)  
	        # 第二层卷积  
	        self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)  
	        # 第二层池化  
	        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)  
	        # 三个全连接层  
	        self.fc1 = nn.Linear(16*5*5, 120)  
	        self.fc2 = nn.Linear(120, 84)  
	        self.fc3 = nn.Linear(84, 10)  
	  
	    def forward(self, x):  
	        x = self.activation(self.conv1(x))  
	        x = self.pool1(x)  
	        x = self.activation(self.conv2(x))  
	        x = self.pool2(x)  
	        x = x.view(x.size(0), -1)  
	        x = self.activation(self.fc1(x))  
	        x = self.activation(self.fc2(x))  
	        x = self.fc3(x)  
	        return x

（2）数据集准备

使用torchvision直接下载Cifar10数据集，设置transform参数为torchvision. transforms.ToTensor()，将图像数据转换为Tensor，数据范围调整到0-1（相当于进行了归一化）。

再使用DataLoader加载数据，设置batch_size为64，在训练集上对数据随机打乱（shuffle=True）以避免过拟合，测试集上则不打乱。

相关设置代码如下：

model = LetNet5(activation=nn.ReLU())  
model.to(device)  # 将模型移动到GPU上  
criterion = nn.CrossEntropyLoss()  
optimizer = torch.optim.Adam(model. Parameters(), lr=0.001)

（4）模型训练与评估

设置epoch为30，训练模型并打印loss和每轮在训练集上的准确率。在测试集上计算准确率并打印。结果如下：

图三：训练30轮结果

可以看到训练集上准确率能达到75%，但是测试集上准确率只有62%。

更改激活函数为Sigmoid和Tanh，训练结果如下：

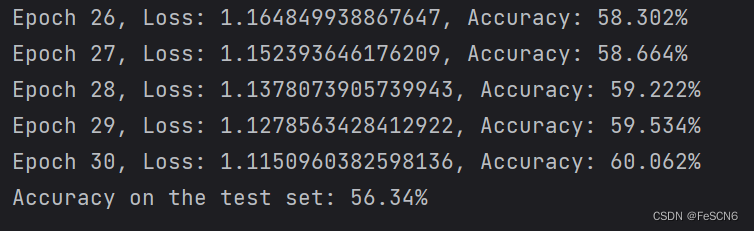
图四：训练30轮结果（Sigmoid）

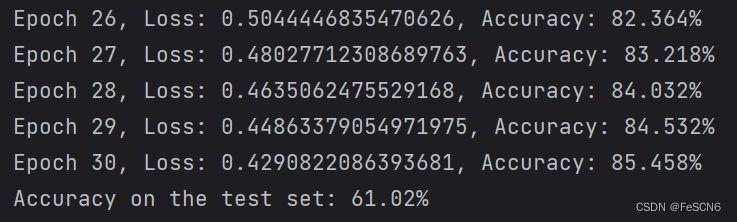
图五：训练30轮结果（Tanh）

比较发现，激活函数为Sigmoid时，在训练集和测试集上的准确率都比较低。而激活函数为Tanh时，训练集上准确率可达85%、测试集上只能达到61%，怀疑发生了过拟合。

2. 对比并分析ReLU、Sigmoid和tanh激活函数对收敛速度的影响，将结果可视化

设置epoch=30，分别使用ReLU, Sigmoid, Tanh激活函数训练模型，可视化训练时的loss变化和训练集上的准确率，结果如下所示：

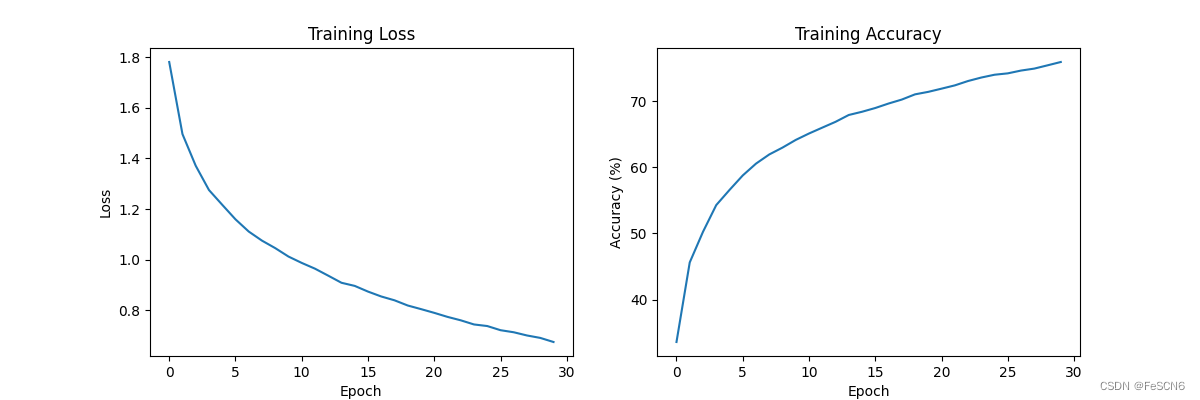
图六：ReLu函数收敛速度及准确率（epoch=30）

图七：Sigmoid函数收敛速度及准确率（epoch=30）

图八：Tanh函数收敛速度及准确率（epoch=30）

通过对比发现，Tanh激活函数收敛速度最快且在训练集上准确率最高，其次是ReLU，最后是Sigmoid。但是课上讲的分析是ReLU 激活函数收敛最快，因为在正数范围内是此函数线性的，而且在负数范围内是零，这样可以减少梯度消失的问题，并且加速了梯度下降的收敛速度。相比之下，Sigmoid 和 Tanh 函数在输入值较大或较小时，梯度较小，容易出现梯度消失问题，且这两个函数计算复杂度较高，所以导致收敛速度较慢。

再对比epoch=10的情况，发现ReLU函数和Tanh收敛速度相差不大，但ReLU稍慢一点。Sigmoid明显收敛速度慢且准确率低。