五、开放空间规划算法
(⼀)开放空间规划算法总体介绍
对于Apollo的算法,⼤部分是在城市结构化道路进⾏规划,开放规划主要应⽤于泊⻋或者靠边停⻋场景
|
|
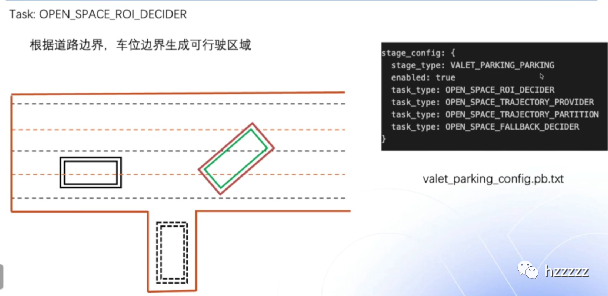
泊⻋场景配置⽂件在上⾯
确定可⾏驶区域,然后规划⽆碰撞的轨迹

⾸先根据HA*和Reeds Sheep曲线,
但是曲线有⼀些突变,不满⾜⻋辆运动学要求需要对轨迹进⾏平滑
|
|
最后检测规划轨迹和障碍物是否进⾏规划,如果失败就重规划
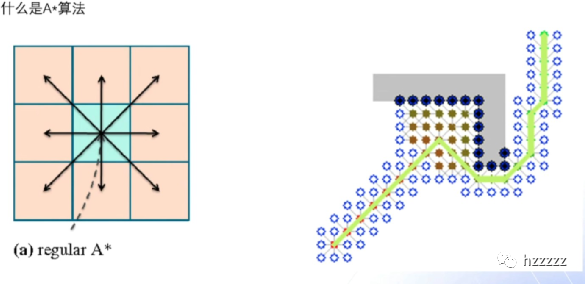
(⼆)基于混合A*的路径规划算法开放空间,A*效率⾼
A*算法流程如下
|
|
A*算法的问题
A*算法产⽣的路径都是折线的,对于⻋辆没法⾛出来
根据⻋辆模型,实际⻋辆航向和后轴中⼼的速度⽅向⼀致
|
|
通过前轮转⾓算出后轮转弯半径,对前轮转⾓进⾏采样,不同前轮转⾓有不同转弯半径,每次向前⾏驶⼀个固定的弧⻓
|
|
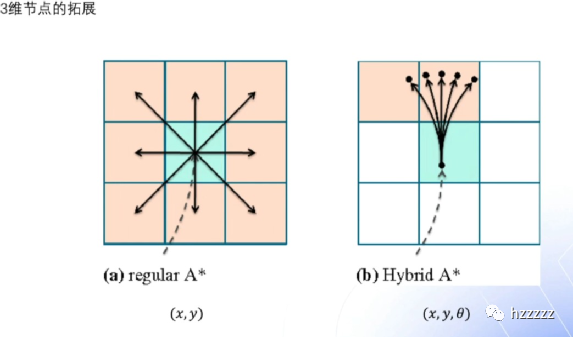
这样得到的路径平滑了很多,但是栅格点不适⽤了,可能⼀个栅格点有多个点所以A*算法的栅格点搜索不适⽤了,从⼆维的xy扩展到xy 航向⾓theta
所以还要定义航向⾓theta的精度,下⾯是Apollo定义的栅格,

其中x_grid, y_grid phi_grid代表xy和航向⾓的索引,也就是xy⽅向的⻓度除以精度, 这⾥通过三个索引组成的字符串来判断节点是否遍历过
我们节点是离散的,⽽状态空间是连续的,导致永远搜不到终点位置和⽅向的
|
|
所以还需要节点的解析拓展

从起点到终点可以以⼀种固定的圆弧和直线连接起来的,有48种线型给出了每种线的解析解,C代表圆弧,|代表改变⽅向。C|C|C代表向左然后这种⽅法没法考虑障碍物的碰撞
所以混合A*还需要考虑障碍物的碰撞检测

代码为例
第⼀步基于动态规划算法,求出每个⼆维节点的代价值,作为启发式函数然后定义两个集合
起点加⼊OpenSet
然后优先队列弹出代价最⼩的
然后起点到终点有没有⽆碰撞的Reed Sheep曲线,如果有的话就退出循环
如果没有的话进⾏节点拓展,如果拓展节点没有被遍历过并且没有障碍物碰撞,加⼊
OpenSet,并计算节点代价值
|
|
效果如下:

后半段是Reed Sheep曲线算的路径
这条路径虽然满⾜⼀些运动学约束,但是还是弧和直线组成,在连接部分还是存在突变,所以还需要轨迹优化,满⾜控制和舒适性的要求
(三)基于OBCA的轨迹规划算法
平滑算法,是基于OBCA的轨迹规划算法
|
|
基于MPC建模,然后⽤优化算法求解。
可以实现横纵向联合规划,也就是考虑速度对路径的影响
回顾以下MPC
|
|
MPC最终也是转换为优化问题,所以也跟其他优化问题⼀样要设计⽬标函数
由于MPC是预测问题,还需要对未来状态进⾏优化求解,需要设计MPC预测模型下⾯说⼀下状态空间⽅程的建⽴
|
|
状态变量是x, y, v, phi
输⼊变量为前轮转⾓和加速度(油门)
然后使⽤模型为⻋辆⽽⾃由度模型,k+1时刻的状态可以由k状态推导⽽来我们需要所有的状态
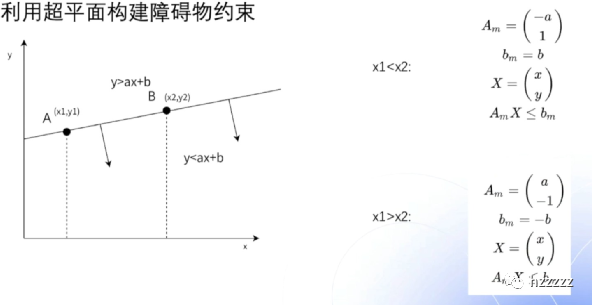
由于OBCA考虑了障碍物的约束,这⾥利⽤超平⾯构建障碍物约束
|
|
如果要表⽰AB曲线下⾯的约束,可以使⽤AX <b< span>来表⽰如果要表⽰障碍物,只需要使⽤四条边联⽴构建即可 </b<>
⾃⻋所占⽤空间,也使⽤超平⾯来表⽰

这⾥B表⽰⾃⻋在原点占⽤的空间
如果⾃⻋在第k时间状态所占⽤的空间,就可以⽤状态旋转矩阵,以及平移矩阵计算出来,包括⻋辆的xy位置和航向⾓
如果要保证主⻋和障碍物不碰撞
|
|
就让他们交集为空即可
定义距离函数dist,就是主⻋沿着任意⽅向t平移和障碍物发⽣接触的范数最⼩的向量下⾯是⼀个等价推论

其中lambda_m和mu_m为拉格朗⽇常数
e’为
|
|
由于范数两个优化变量不太好算,所以引⼊新的变量w以及等式约束

然后得到下⾯这个问题,就是w⼆范数最⼩的时候
有条件的极值问题(原问题)转换为⽆条件的极值问题(对偶问题) 原问题有⼀个⽬标函数,以及等式约束和不等式约束
|
|
对于原问题得到求出拉格朗⽇函数
|
|
通过拉格朗⽇函数就可以把有条件的极值问题(原问题)转换为⽆条件的极值问题
(对偶问题)
接下来把拉格朗⽇函数的lambda 和 nu 看作常量,然后在x定义域内求极⼩值得到对偶函数
|
|
原问题的对偶问题就是拉格朗⽇函数取极⼤值的过程
|
|
原问题的最优解为p^*,对偶问题的最优解为d^*,有p^* ≥ d^* 成⽴
如果原问题是凸问题,等式成⽴,也就是p^* = d^*,也就是⼀个强对偶问题
接下来回到研究的问题,三个约束函数,引⼊三个拉格朗⽇乘⼦,求拉格朗⽇对偶函数
|
|
g的第⼀项为⽬标函数,后⾯三项是拉格朗⽇乘数乘以约束函数然后求解o’和w的下确界的函数
|
|
前两项都是线性函数,要使他们下确界存在,系数就得等于零,得到两个公式
对于第三项,⼜因为范数的共轭函数性质,根据凸优化理论,要么等于0要么-∞,要让下确界存在就得等于0
就剩下后⾯这⼀项了
|
|
对偶问题的最优解就是原问题的最优解,只要保证d*>d_min,就可以保证原问题
>d_min
也就是取最⼤值的lambda和miu的取值:存在⼀组lambda和miu,使得不等式成⽴就可以
所以在MPC的约束设计中,如果要使得障碍物不碰撞,就要有以下不等式成⽴,作为碰撞约束
|
|
另外还需要起点和终点的约束
|
|
然后每个点要满⾜⻋辆运动学约束,也就是xk+1和xk的关系

此外还要满⾜规划的极限,速度要在范围内,xy在可⾏驶区域内,航向⾓可以任意取值
|
|
输⼊量也在范围内
前轮转⾓和加减速度,此外横摆⾓速度也要满⾜
|
|
MPC的⽬标函数设计
对预测时域每个状态的xk的损失求和

损失函数的第⼀项就是⻋辆跟踪参考路径的变化舒适性:加速度越⼩越好
帧间连续性:MPC的第⼀个输⼊分量要和当前状态尽可能接近输⼊量变化率尽可能⼩
|
|
得到cost函数
|
|
⽤⼆范数表⽰每⼀个cost项
最后OBCA转化为⼀个⾮线性的优化问题
|
|
然后使⽤IPOPT进⾏求解
如果有⼀个好的初始解,就可以加快解的速度,所以使⽤混合A*算法的轨迹作为初始解
此外,对偶变量还有⼀个初始解
对偶变量的初始化,使⽤碰撞约束的对偶函数优化求解,
|
|
根据对偶函数设计,把都偶函数⽤-dmk表⽰,这样就把极⼤值问题转换为极⼩值问题进⾏求解,⽅便带⼊IPOPT
对每个时间k的每个障碍物距离,求和,取最⼩值
求出的⽬标函数最⼩值的mu和lambda,就是对偶变量的初始解的值
|
|
但是经过分析,这⾥⾯约束有⼀个⼆次函数,因此使⽤⾮线性求解器求解,为了提⾼求解效率,Apollo进⾏了⼀个优化,就是把⼆次约束放到约束函数⾥⾯成为软约束, 这样就变成⼆次规划问题,使⽤OSQP求解

此外还有⼀些衍⽣算法, 第⼀个是采样时间可变,
|
|
⽆论如何优化都是在最后时间到达终点,这⾥可以增加⼀个采样时间系数t(k),从固定的ts变化成ts*t(k),这样可以缩短时间
|
|
约束函数替换成了ts*t(k) 约束函数也变化成
|
|
⽬标函数也增加惩罚,希望系数越⼩越好下⾯是终点松弛

终点如果是硬约束会让求解变慢,甚⾄⽆解
到达终点附近也是能满⾜需求的,因此把硬约束转换成软约束,增加到达终点状态的惩罚项,增加松弛
(四)基于DL-IAPS的路径规划算法
虽然OBCA算法很好解决了开放空间规划,但是算法效率和鲁棒性有限
|
|
Apollo设计了横纵向解耦的开放空间轨迹规划算法
分段的平滑算法,OBCA整条⼀起平滑,DL-IAPS是把前进倒⻋等分段进⾏平滑,同时保证平滑后的路径不碰撞

对于速度规划使⽤PJSO算法,也就是分段Jerk Speed Opt DL-IAPS 双循环迭代锚点路径平滑算法
外层循环是检测碰撞,内层循环是平滑
设计了⼀种迭代的⽅法来求解障碍物约束参考对于散点的位置约束
|
|
在 DL-IAPS 种使⽤类似⽅法对路径进⾏平滑,
|
|
平滑结果后将和障碍物进⾏碰撞检查,如果检测发⽣碰撞,就把碰撞的参考点调⼩矩形块的⼤⼩重新进⾏下⼀次平滑。不断迭代直到满⾜碰撞约束为⽌。
参考线平滑算法中,考虑了曲率约束,但是是⾮线性的
|
|
参考线平滑点的数量多,对实时性要求⾼,所以不考虑曲率约束
但是在开放规划中,本⾝曲率是⽐较⾼的,所以必须要考虑曲率约束采⽤了⼀种序列⼆次规划

对约束函数进⾏线性化,保留⼀次项得到下⾯的式⼦
|
|
使⽤上轮迭代结果,同时对优化点增加可信区间约束优化问题简化成⼆次规划问题
|
|
算法整体架构如下

(五)开放空间规划算法实践





























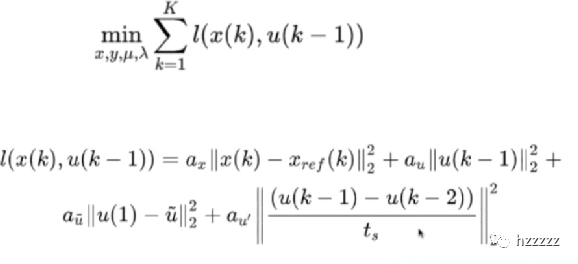









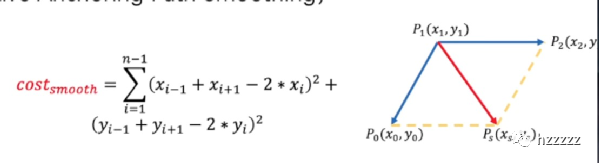


















 719
719

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








