最优化方法线性方程组求解

最新推荐文章于 2025-01-06 06:30:00 发布

KING BOB!!!

最新推荐文章于 2025-01-06 06:30:00 发布

阅读量936

点赞数 1

分类专栏：最优化方法文章标签：性能优化 matlab 线性代数

本文链接：https://blog.csdn.net/m0_62895602/article/details/133744219

版权

最优化方法专栏收录该内容

1 篇文章

订阅专栏

最优化方法线性方程组求解

高斯消元法求解线性方程组

问题

已知向量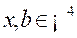，矩阵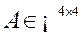，线性方程组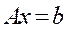，其中：

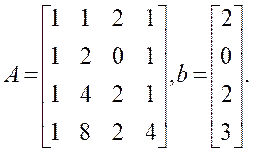
编写代码，通过高斯消元法求解,并验证解的准确性。

求解过程

高斯消元法是一种解线性方程组的常用方法，它的基本原理是通过一系列的行变换将原始方程组转化为一个上三角形方程组，然后通过回代求解得到方程组的解。

考虑一个线性方程组Ax=b，其中A是一个4×4的矩阵，b是一个4维的列向量，要求解x。

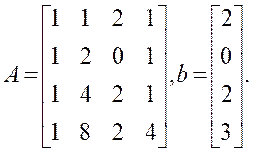
化为增广矩阵：

将方程组化为增广矩阵[A | b]，也就是将矩阵A和向量b合并成一个4×5的矩阵。

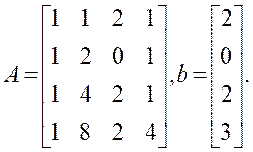
选择主元：

选取第一列中的一个非零元素作为主元，通常选择第一行第一列的元素（A[1][1]）。如果主元为零，则可以选择下一列中的非零元素，或者进行行交换来选取一个非零主元。

消元操作：

确定主元后，需要进行一系列的行操作，将主元所在列的其他元素变为零。这些行操作包括：

将主元所在行的所有元素除以主元的值，以确保主元变为1。
对于主元所在列的其他行，通过将主元所在行的适当倍数加到这些行上，使得主元所在列的其他元素都变为零。

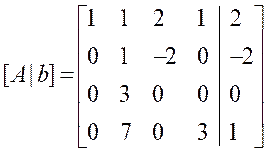
这一步的目标是将矩阵转化为上三角形矩阵，即主对角线以下的所有元素都变为零。

重复步骤2和步骤3：继续选择下一列的主元，然后进行相应的消元操作，直到将整个矩阵转化为上三角形矩阵。

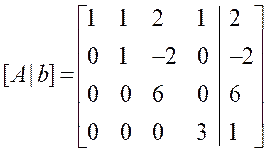
回代求解：

一旦矩阵被转化为上三角形矩阵，就可以使用回代方法求解方程组。从最后一行开始，依次求解每个未知数。具体步骤如下：

对于最后一行，直接通过等式求解最后一个未知数。

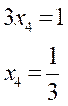
对于倒数第二行，先求解倒数第二个未知数，然后带入已经求解出的未知数来求解下一个未知数。

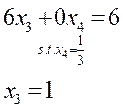
依此类推，一直求解到第一个未知数。

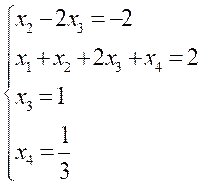
得到解向量：完成回代步骤后，你将得到方程组的解向量x。

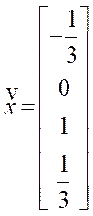
clc;
clear;
close all;
A = [1,1,2,1;1,2,0,1;1,4,2,1;1,8,2,4];
b = [2; 0; 2; 3];
x = gauss_(A, b);
disp(x);
% save('x.mat', 'x', 'x');
% 计算等式左侧

% 验证解的正确性
% 检查左侧和右侧是否近似相等
left_side = A * x;
tolerance = 1e-6; % 设置一个小的容忍误差
is_correct = all(abs(left_side - b) < tolerance);
if is_correct
    disp('x 是正确的解。');
else
    disp('x 不是正确的解。');
end

function x = gauss_(A, b)    
    [m, n] = size(A);
    if m ~= n
        error('系数矩阵必须是方阵');
    end
    % 增广矩阵 [A | b]
    augmented_matrix = [A, b];
    % 初等行变换将增广矩阵转化为上三角形矩阵
    for i = 1:n      
        % 将当前列的第一个元素缩放为1
        augmented_matrix(i, :) = augmented_matrix(i, :) / augmented_matrix(i, i);
        % 利用当前行的第一个元素，将下面的行消元为零
        for j = i+1:n
            augmented_matrix(j, :) = augmented_matrix(j, :) - augmented_matrix(i, :) * augmented_matrix(j, i);
        end
    end
    % 回代求解
    x = zeros(n, 1);
    for i = n:-1:1
        x(i) = augmented_matrix(i, end) - augmented_matrix(i, i+1:end-1) * x(i+1:end);
    end
end

高斯消元法求解矩阵的逆

问题

是否可以通过高斯消元法，构造线性方程组求矩阵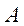的逆？如果可以求其逆矩阵。

求解过程

构造一个增广矩阵，右边是单位矩阵I。也就是将[A | I]组成一个4×8的矩阵。

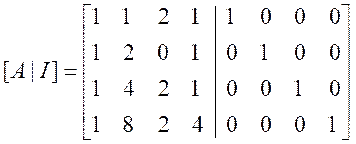
使用高斯消元法，进行行变换，将增广矩阵变换为上三角形形式，

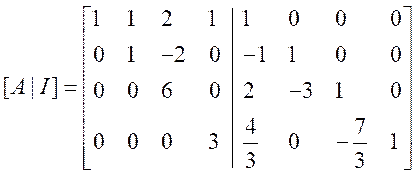
进行行变换，确保左半部分（原始矩阵A的部分）变为单位矩阵。

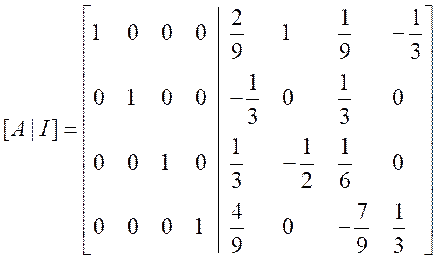
此时，右半部分将包含矩阵A的逆矩阵。将右半部分提取出来，即得到了矩阵A的逆矩阵。

clc;
clear;
close all;
A = [1,1,2,1;1,2,0,1;1,4,2,1;1,8,2,4];
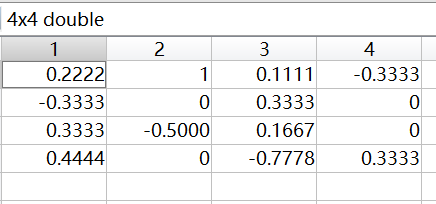
A_inv = gauss_inv(A);
disp(A_inv);

% 验证解的正确性
left_side = A * A_inv;
% 检查左侧和右侧是否近似相等
tolerance = 1e-6; % 设置一个小的容忍误差
is_correct = all(abs(left_side - eye(4)) < tolerance);
if is_correct
    disp('x 是正确的解。');
else
    disp('x 不是正确的解。');
end

function A_inv = gauss_inv(A)    
    [m, n] = size(A);
    if m ~= n
        error('输入矩阵必须是方阵');
    end
    % 构建增广矩阵 [A | I], 其中 I 是单位矩阵
    augmented_matrix = [A, eye(n)];
    % 初等行变换将增广矩阵转化为对角矩阵
    for i = 1:n
        % 将当前列的第一个元素缩放为1
        augmented_matrix(i, :) = augmented_matrix(i, :) / augmented_matrix(i, i);
        % 利用当前行的第一个元素，将下面的行消元为零
        for j = 1:n
            if j ~= i
                augmented_matrix(j, :) = augmented_matrix(j, :) - augmented_matrix(i, :) * augmented_matrix(j, i);
            end
        end
    end
    % 提取逆矩阵部分
    A_inv = augmented_matrix(:, n+1:end);
end

改进：

在传统的高斯消元法求解矩阵的逆的过程中，将原矩阵转换为单位阵这一步骤时间复杂度较大，为此我们可以改为逐列求解矩阵的逆

比如：对于矩阵A，我们想要求解 $A^{-1}$

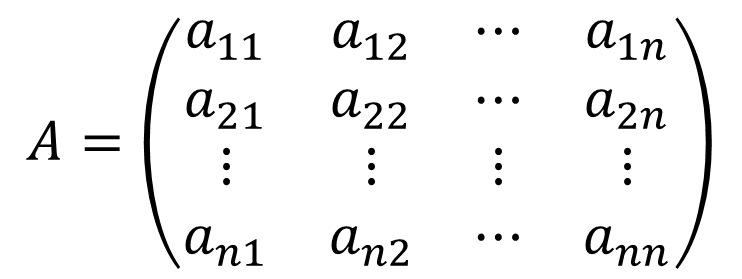
假设

则有
$Ax^j=y^j$
其中

因此，我们只需要将 $A^{-1}$ 的每一列都当作线性方程组 $Ax^j=y^j$ 的解，然后将每列解合并在一起即为 $A^{-1}$

为此我们可以构造增广矩阵[A|I]，然后用高斯消元法将A转换为上三角阵的形式，此时我们不需要再将A转换为单位矩阵，而是直接对该增广矩阵求解线性方程组，得到一个矩阵形式的解（区别于之前向量形式的解），这个矩阵就是 $A^{-1}$

clc;
clear;
close all;
A = [1,1,2,1;1,2,0,1;1,4,2,1;1,8,2,4];
x = gauss_inv2(A);

function x = gauss_inv2(A) %高斯消元法求逆
    [m, n] = size(A);
    if m ~= n
        error('系数矩阵必须是方阵');
    end
    % 增广矩阵 [A | b]
    I = eye(m);
    augmented_matrix = [A, I];
    % 初等行变换将增广矩阵转化为上三角形矩阵
    for i = 1:n      
        % 将当前列的第一个元素缩放为1
        augmented_matrix(i, :) = augmented_matrix(i, :) / augmented_matrix(i, i);
        % 利用当前行的第一个元素，将下面的行消元为零
        for j = i+1:n
            augmented_matrix(j, :) = augmented_matrix(j, :) - augmented_matrix(i, :) * augmented_matrix(j, i);
        end
    end
    % 回代求解
    x = zeros(n, n);
    for i = n:-1:1
        x(i, :) = augmented_matrix(i, n+1:end) - augmented_matrix(i, i+1:n) * x(i+1:end, :);
    end
end

测试性能

clc;clear;close all;
result = zeros(2, 15);
for i = 100:100:1500
    % 产生随机矩阵
    A = randi([1, 100], i, i);
    tic;
    A_inv1 = Gauss_inv1(A);
    end_time1 = toc;
    tic;
    A_inv2 = Gauss_inv2(A);
    end_time2 = toc;
    result(1, i/100) = end_time1;
    result(2, i/100) = end_time2;
end
disp(result)

% 传统高斯消元法求逆
function A_inv = Gauss_inv1(A)    
    [m, n] = size(A);
    if m ~= n
        error('输入矩阵必须是方阵');
    end
    % 构建增广矩阵 [A | I], 其中 I 是单位矩阵
    augmented_matrix = [A, eye(n)];
    % 初等行变换将增广矩阵转化为对角矩阵
    for i = 1:n
        % 将当前列的第一个元素缩放为1
        augmented_matrix(i, :) = augmented_matrix(i, :) / augmented_matrix(i, i);
        % 利用当前行的第一个元素，将下面的行消元为零
        for j = 1:n
            if j ~= i
                augmented_matrix(j, :) = augmented_matrix(j, :) - augmented_matrix(i, :) * augmented_matrix(j, i);
            end
        end
    end
    % 提取逆矩阵部分
    A_inv = augmented_matrix(:, n+1:end);
end


% 改进的高斯消元法求逆
function x = Gauss_inv2(A) 
    [m, n] = size(A);
    if m ~= n
        error('系数矩阵必须是方阵');
    end
    % 增广矩阵 [A | b]
    I = eye(m);
    augmented_matrix = [A, I];
    % 初等行变换将增广矩阵转化为上三角形矩阵
    for i = 1:n      
        % 将当前列的第一个元素缩放为1
        augmented_matrix(i, :) = augmented_matrix(i, :) / augmented_matrix(i, i);
        % 利用当前行的第一个元素，将下面的行消元为零
        for j = i+1:n
            augmented_matrix(j, :) = augmented_matrix(j, :) - augmented_matrix(i, :) * augmented_matrix(j, i);
        end
    end
    % 回代求解
    x = zeros(n, n);
    for i = n:-1:1
        x(i, :) = augmented_matrix(i, n+1:end) - augmented_matrix(i, i+1:n) * x(i+1:end, :);
    end
end

不难看出，随着矩阵维度数的增加，改进后的高斯消元求逆运行的时间要比传统方法更短，性能更强

高斯列主消元法

问题：

因为计算机存在舍入误差，若主元很小，趋近于0时，使用传统高斯消元法将主元作为除数可能会导致其他行的元素误差放大。

求解过程：

高斯列主消元法是一种用于解决线性方程组的数值方法。它是高斯消元法的一种改进版本，用于避免或减小数值不稳定性，以下是使用高斯列主消元法求解线性方程组的一般步骤：

**以三位有效数字为例，**对于一个线性方程组Bx = b，其中B是系数矩阵，x是未知向量，b是右侧常数向量。

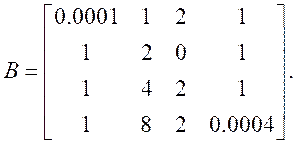
构造增广矩阵：

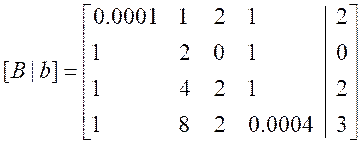
主元素选择：

在每一列上选择主元素，通常选择每一列中绝对值最大的元素作为主元素。
为了避免除以零的情况，可以使用部分主元素选择，交换当前列及以下行中主元素所在的行，确保主元素不为零。

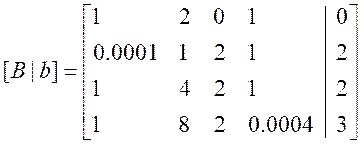
行交换：

如果在部分主元素选择的过程中，需要交换行以确保主元素不为零，则执行行交换操作，以确保主元素在该列的上方。

消元：

从第一列开始，使用主元素所在的行来消除下面的行中的元素，使得主元素下方的元素都为零。这可以通过将适当的倍数的主元素所在行添加到下面的行上来实现。

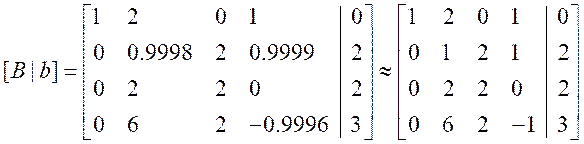
2. 重复步骤1继续选择下一列的主元，然后进行相应的消元操作，直到将整个矩阵转化为上三角形矩阵。

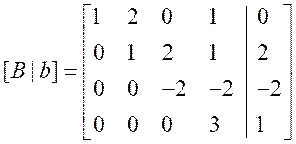
回代：

一旦完成消元过程，得到一个上三角矩阵（或者称为行阶梯形式），然后可以使用回代法来解决方程组。从最后一行开始，通过依次代入已知的变量值，计算出未知变量的值。

clc;
clear;
close all;
A = [0.0001 1 2 1; 1 2 0 1; 1 4 2 1; 1 8 2 0.0004];
% 三位有效小数位
A_round = round(A, 3);
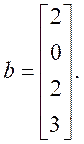
b = [2; 0; 2; 3];
x_correct = gauss_col(A, b);
x1 = gauss_(A_round, b);
x2 = gauss_col(A_round, b);
disp(x_correct);
disp(x1);
disp(x2);



% 顺序高斯消元法
function x = gauss_(A, b)    
    [m, n] = size(A);
    if m ~= n
        error('系数矩阵必须是方阵');
    end
    % 增广矩阵 [A | b]
    augmented_matrix = [A, b];
    % 初等行变换将增广矩阵转化为上三角形矩阵
    for i = 1:n      
        % 将当前列的第一个元素缩放为1
        augmented_matrix(i, :) = augmented_matrix(i, :) / augmented_matrix(i, i);
        % 利用当前行的第一个元素，将下面的行消元为零
        for j = i+1:n
            augmented_matrix(j, :) = augmented_matrix(j, :) - augmented_matrix(i, :) * augmented_matrix(j, i);
        end
    end
    % 回代求解
    x = zeros(n, 1);
    for i = n:-1:1
        x(i) = augmented_matrix(i, end) - augmented_matrix(i, i+1:end-1) * x(i+1:end);
    end
end

% 高斯列主消元法
function x = gauss_col(A, b)    
    [m, n] = size(A);
    if m ~= n
        error('系数矩阵必须是方阵');
    end
    % 增广矩阵 [A | b]
    augmented_matrix = [A, b];
    % 初等行变换将增广矩阵转化为上三角形矩阵
    for i = 1:n
        % 找到当前列中绝对值最大的元素所在的行
        [~, max_row] = max(abs(augmented_matrix(i:n, i)));
        max_row = max_row + i - 1;
        % 交换当前行与最大值所在行
        augmented_matrix([i, max_row], :) = augmented_matrix([max_row, i], :);        
        % 将当前列的第一个元素缩放为1
        augmented_matrix(i, :) = augmented_matrix(i, :) / augmented_matrix(i, i);
        % 利用当前行的第一个元素，将下面的行消元为零
        for j = i+1:n
            augmented_matrix(j, :) = augmented_matrix(j, :) - augmented_matrix(i, :) * augmented_matrix(j, i);
        end
    end
    % 回代求解
    x = zeros(n, 1);
    for i = n:-1:1
        x(i) = augmented_matrix(i, end) - augmented_matrix(i, i+1:end-1) * x(i+1:end);
    end
end