数学建模——插值（下）

七七喝椰奶

已于 2023-09-10 12:07:51 修改

阅读量2.4k

点赞数 1

分类专栏：数学建模文章标签：数学建模算法

于 2023-07-04 16:17:22 首次发布

本文链接：https://blog.csdn.net/m0_63024355/article/details/131506321

版权

数学建模专栏收录该内容

28 篇文章 6 订阅

订阅专栏

本文是面向数学建模准备的，是介绍性文章，没有过多关于原理的说明！！！

1、已知网格节点(xi,yj,zij)(i=1,2,…,m,j=1,2,…,n),且满足

一、2维插值原理及公式

1、二维插值问题

已知网格节点(xi,yj,zij)(i=1,2,…,m,j=1,2,…,n),且满足

求点(x,y)处的插值z。

2、最邻近插值

如下图所示，将四个插值节点所围成的矩形区域分成四个部分，待插值点(x,y)落在哪个区域，就用哪个顶点的函数值作为(x,y)的函数值z。

优点：快速、方便计算

缺点：不连续，图像阶梯状

3、分片线性插值

如下图所示，记四个插值节点的函数值为

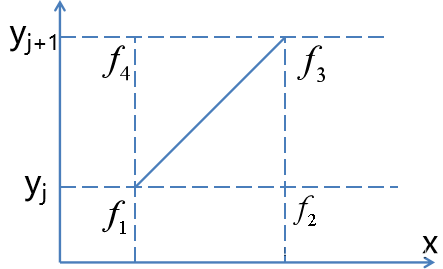
（1）当待插值点位于下三角，即

待插点(x,y)的函数值为

（2）当待插值点位于上三角，即

待插点(x,y)的函数值为

优点：插值函数连续；

缺点：插值面不光滑；

4、双线性插值

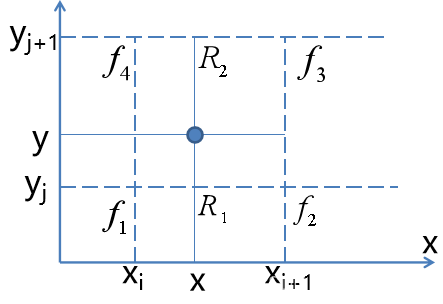
双线性插值，是一片一片二次曲面构成。如上图所示，设

（1）线性插入R1,R2的值

（2）计算待插点的函数值

优点：便于计算

缺点：节点处不一定光滑

5、二维样条插值

如上图，二维样条插值步骤：

（1）用f1,f2一维样条插值估计f(R1);

（2）用f3,f4一维样条插值估计f(R2);

（3）用R1,R2一维样条插值计算f(x,y)的值。

优点：插值点二阶偏导数连续。

二、二维插值及其Matlab工具箱

1、插值节点顺序

已知网格节点(xi,yj,zij)(i=1,2,…,m,j=1,2,…,n),且满足

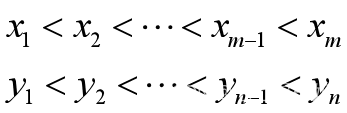
求点(x,y)处的插值z

Matlab工具箱调用格式（1）

z=interp2(x0,y0,z0,x,y,'method')

参数介绍：

x0,y0为m维和n维向量
z0是n×m矩阵，表示节点值
x,y为一维数组，表示插值点，x是行向量，y是列向量，z是矩阵，它的行数是y的维数，列数是x的维数
‘method’的取值常用的插值方法包括 ‘linear’（线性插值）、‘cubic’（立方插值）、‘nearest’（最近邻插值）等。

方法介绍：

线性插值（‘linear’）：
线性插值是最简单和常用的插值方法。它假设在数据点之间的区域内，数据是按线性方式变化的。线性插值使用相邻数据点之间的直线，通过计算目标位置处的加权平均值来估计目标位置的值。线性插值方法简单快速，但可能无法很好地逼近复杂的数据模式。

立方插值（‘cubic’）：
立方插值使用了更复杂的插值模型，以逼近数据点之间的值。它使用一个立方函数来估计目标位置处的值，不仅考虑了相邻数据点的值，还考虑了相邻数据点的梯度。立方插值在保持平滑性的同时，能够更好地逼近曲线和曲面的变化。它通常比线性插值精确，但计算更复杂。

最近邻插值（‘nearest’）：
最近邻插值是一种简单的插值方法，它使用最近的数据点的值作为目标位置的估计值。在最近邻插值中，目标位置被分配为最接近的数据点之一的值。这种插值方法计算简单且快速，但可能产生较大的误差，特别是在数据变化较大的区域。

调用格式(三次样条插值法）2

pp=csape({x0,y0},z0,conds,valconds)；

z=fnval(pp,{x,y})；

参数介绍：

{x0, y0}：一个包含 x 坐标和 y 坐标数据点的 cell 数组。x0 是一个向量，包含原始数据点的 x 坐标，y0 是一个向量，包含原始数据点的 y 坐标。这些数据点用于构建三次样条插值曲线。
z0：一个和 {x0, y0} 大小相匹配的矩阵或数组，包含原始数据点的对应值。
conds：一个可选参数，定义了曲线的边界条件。它可以是字符串 'clamped' 或 'complete'。
valconds：一个可选参数，用于定义插值结果在曲线的边界点上的导数值或值。这取决于 conds 参数的指定。