《信息论》研讨--信息论的深度学习模型理解

噢4u

已于 2024-12-30 04:16:53 修改

阅读量2k

点赞数 50

分类专栏：我の论文阅读从0开始学习机器学习文章标签：深度学习信息论人工智能

于 2024-12-11 16:29:47 首次发布

本文链接：https://blog.csdn.net/m0_73752612/article/details/144401474

版权

从0开始学习机器学习同时被 2 个专栏收录

29 篇文章

订阅专栏

我の论文阅读

3 篇文章

订阅专栏

论文内容概述

1. 《ON THE INFORMATION BOTTLENECK THEORY OF DEEP LEARNING》

中文标题：关于深度学习中信息瓶颈理论的研究

背景与问题：
信息瓶颈（Information Bottleneck, IB）理论为理解深度学习模型的训练过程和泛化能力提供了重要框架。然而，IB理论在不同深度网络架构和任务中的适用性及其解释力尚未完全明确。
研究问题：
1. 深度网络在训练过程中是否经历明显的信息压缩阶段？
2. 信息瓶颈理论能否有效解释深度学习模型的泛化现象？
3. 不同网络架构和优化算法下的信息流动模式有何不同？
提出的方法：
作者系统性地评估信息瓶颈理论在多种深度网络架构（如卷积神经网络、全连接网络）和不同优化策略（如SGD、Adam）下的表现。通过理论分析与实验验证，研究网络训练过程中互信息 I(X;T) 和 I(T;Y)的动态变化，其中 T 表示中间层的表示。
主要定理与引理：
- 定理1：在具有充分表示能力的深度网络中，训练初期，互信息 I(X;T) 和 I(T;Y) 均显著增加，随后 I(X;T) 开始下降，而 I(T;Y) 继续保持或略有下降。
- 引理1：在特定网络架构下，信息压缩阶段的出现依赖于激活函数的性质和网络的非线性程度。
具体结论：
信息瓶颈理论在解释深度学习模型的训练动态和泛化能力方面具有一定的有效性，特别是在具有非线性激活函数和足够深度的网络中。信息压缩现象在这些条件下显著，有助于模型抑制无关信息，提升泛化性能。然而，在线性或浅层网络中，信息压缩现象不明显，IB理论的解释力受限。
具体指导：
1. 网络设计：建议在深度网络中引入非线性激活函数和适当的正则化策略，以促进信息压缩和泛化能力提升。
2. 优化策略：采用具有稳定性和适应性的优化算法（如Adam），有助于更好地实现信息瓶颈目标。
3. 进一步研究方向：探索信息瓶颈在不同任务（如生成模型、强化学习）中的应用，以及与其他理论框架（如统计学习理论）的结合。

2. 《Explaining A Black-box By Using A Deep Variational Information Bottleneck Approach》

中文标题：利用深度变分信息瓶颈方法对黑箱模型进行解释

背景与问题：
深度学习模型通常被视为黑箱，其内部决策机制难以解释。信息瓶颈方法提供了一种理论工具，通过分析输入与输出之间的关键信息，提升模型的可解释性。
研究问题：
如何通过信息瓶颈方法解释深度学习模型的内部机制，揭示模型在决策过程中依赖的关键特征，从而提升模型的可解释性？
提出的方法（DVIB框架）：
深度变分信息瓶颈（Deep Variational Information Bottleneck, DVIB）框架通过引入中间表示 Z 来优化输入 X 与输出 Y 之间的信息传递。其目标函数为：

其中，β是权衡参数，用于平衡信息保留与信息压缩。具体实现步骤包括：
1. 神经网络参数化：使用神经网络分别参数化 p(z∣x) 和 p(y∣z)。
2. 变分推断：引入变分下界（Variational Lower Bound）以近似互信息，利用重参数化技巧（Reparameterization Trick）优化网络参数。
3. 优化过程：通过梯度上升最大化 I(Z;Y) 并最小化 I(Z;X)，实现对中间表示 Z 的有效提取和压缩。
主要定理与引理：
- 定理1：DVIB框架通过变分下界优化，可以有效逼近原始信息瓶颈目标，确保 Z 保留关键的任务相关信息。
- 引理1：在有限样本条件下，DVIB的变分下界具有较好的收敛性，保证模型在实际应用中的稳定性。
具体结论：
DVIB方法能够在保持模型预测性能的同时，显著提高模型的可解释性。通过分析中间表示 Z，可以识别出对最终预测最具影响力的输入特征。实验结果表明，DVIB在多个数据集上均表现出优越的解释能力，验证了其在解释深度黑箱模型中的有效性。
具体指导：
1. 模型解释：通过引入DVIB框架，可以系统性地分析深度模型的决策依据，识别关键特征，提升模型的透明度。
2. 特征选择：利用DVIB提取的中间表示 Z，可以进行更加有效的特征选择，过滤掉无关信息，提升模型的泛化能力。
3. 进一步研究方向：探索DVIB在不同类型深度模型（如卷积神经网络、循环神经网络）中的应用，以及与其他解释方法（如注意力机制）的结合。

3. 《Opening the Black Box of Deep Neural Networks via Information》

中文标题：通过信息论方法揭开深度神经网络的黑箱

背景与问题：
深度神经网络（Deep Neural Networks, DNNs）的复杂层级结构使得其内部工作机制难以理解。信息论提供了一种有效的工具，用于分析和揭示网络内部的信息流动和表示学习过程。
研究问题：
如何利用信息论方法，揭示深度神经网络内部的信息传递和表示学习过程，解释其黑箱特性？
研究方法与具体步骤：
1. 信息瓶颈框架应用：将信息瓶颈理论应用于深度网络的各层，定义中间层表示为 TT，并计算 I(X;T) 和 I(T;Y)。
2. 训练过程分析：监测训练过程中各层的互信息变化，观察信息在网络中的传递与压缩。
3. 实验设计：在不同网络架构和数据集上进行实验，系统性地分析信息流动模式。
主要发现：
- 训练阶段划分：深度网络的训练过程分为两个显著阶段：
  1. 拟合阶段（Fitting Phase）：网络快速拟合训练数据，I(T;Y) 显著增加，网络逐步学习到任务相关的信息。
  2. 压缩阶段（Compression Phase）：随着训练的继续，网络逐步压缩中间表示中的无关信息，I(X;T) 逐渐减少，同时 I(T;Y) 保持稳定或略有下降。
- 泛化能力提升：信息压缩阶段有助于网络抑制噪声和冗余信息，提升模型的泛化能力。
具体结论：
信息瓶颈理论成功解释了深度神经网络在训练过程中如何通过信息压缩提取有用特征，从而提升泛化能力。研究表明，深度网络通过先拟合再压缩的训练动态，能够自主过滤掉与任务无关的信息，解释了其在复杂任务中的优越表现。
具体指导：
1. 训练策略优化：根据信息瓶颈的训练动态，设计优化策略，如适当调整学习率和正则化参数，以促进有效的信息压缩。
2. 网络架构设计：构建具有良好信息传递和压缩能力的网络架构，例如通过增加瓶颈层或使用特定的激活函数来促进信息压缩。
3. 进一步研究方向：深入探讨信息瓶颈在不同类型任务（如自然语言处理、计算机视觉）中的具体作用机制，以及其与其他正则化方法（如Dropout、Batch Normalization）的相互关系。

4. 《DO GANS LEARN THE DISTRIBUTION? SOME THEORY AND EMPIRICS》

中文标题：GAN是否真正学到了分布？一些理论与实证分析

背景与问题：
生成对抗网络（Generative Adversarial Networks, GANs）在生成模型领域取得了巨大成功，但关于GANs是否能够从有限样本中真正学习并逼近目标分布仍存在争议。理论基础尚不完全清晰，尤其是在高维复杂数据中的表现。
研究问题：
GANs是否具备从有限样本中学习并逼近真实数据分布的能力？其性能受哪些因素影响？
提出的理论框架：
作者从以下几个方面对GANs进行理论分析：
1. 表示能力：分析生成器网络是否具备足够的表达能力来刻画目标分布，探讨网络深度、宽度与分布复杂度之间的关系。
2. 优化与收敛性：研究在给定判别器和生成器容量的条件下，GAN的训练过程是否能够收敛到纳什均衡，并逼近真实分布。
3. 样本复杂性与通用化：分析GAN在有限样本条件下学习复杂分布的可能性，探讨模式坍缩（mode collapse）等问题的理论基础。
具体理论内容：
- 定理1：在生成器和判别器具备无限表示能力且训练达到纳什均衡时，GAN的生成分布等于真实数据分布。
- 定理2：对于有限容量的生成器和判别器，存在一个界限，描述生成分布与真实分布之间的差异，该差异依赖于网络的容量和训练样本量。
- 引理1：在高维空间中，GAN的样本复杂性随着数据分布的复杂度（如多模态分布）指数级增长，导致训练难度显著增加。
实验与结论：
实验部分通过多种数据分布（包括高维多模态分布）对GAN进行训练，评估其逼近真实分布的能力。结果表明：
- 理论验证：在理论假设（如无限网络容量、理想优化条件）下，GAN能够成功逼近真实分布。
- 实际表现：在实际应用中，受限于网络结构、训练算法和数据复杂度，GAN常出现模式坍缩、未能覆盖全部数据模态等问题，导致生成分布与真实分布存在明显差异。
具体结论与指导：
- 结论：GANs在理论上具备学习真实数据分布的能力，但在实际应用中受到多种因素的限制，导致其在高维复杂数据中的表现不尽如人意。
- 具体指导：
  1. 网络架构改进：设计更具表达能力和稳定性的生成器与判别器结构，如引入残差连接、渐进式训练等方法，以提升GAN的分布逼近能力。
  2. 优化算法优化：采用更加稳定和高效的优化算法，如使用谱归一化（Spectral Normalization）、梯度惩罚（Gradient Penalty）等技术，防止模式坍缩和梯度消失问题。
  3. 正则化与多样性激励：引入正则化项和多样性激励机制，鼓励生成器覆盖更多数据模态，避免模式坍缩现象。
  4. 进一步研究方向：探索GAN与其他生成模型（如VAE、Flow-based Models）的结合，提升生成模型的整体表现；研究在不同任务和数据分布下GAN的适用性与优化策略。

5. 《Mutual Information Neural Estimation (MINE)》

中文标题：互信息的神经估计

背景与问题：
互信息（Mutual Information, MI）是衡量两个随机变量间依赖关系的重要信息论量。然而，在高维数据中直接估计互信息极为困难，传统方法在维度增加时表现不佳，难以有效应用于复杂机器学习模型。
研究问题：
如何设计一种高效、准确的互信息估计算法，能够在高维复杂数据中有效应用，并克服传统方法的限制？
提出的方法（MINE）：
互信息神经估计（Mutual Information Neural Estimation, MINE）利用神经网络来估计互信息的一个下界，具体步骤如下：
1. Donsker-Varadhan 表示：利用Donsker-Varadhan变分下界，将互信息 I(X;Y)表示为： $I(X; Y) \geq \sup_{f \in \mathcal{F}} \mathbb{E}_{p(x,y)}[f(x,y)] - \log(\mathbb{E}_{p(x)p(y)}[e^{f(x,y)}])$ 其中， $\mathcal{F}$ 是一组可参数化的函数。
2. 神经网络参数化：将函数 f 参数化为一个可训练的神经网络 $f_\theta(x, y)$ ，并通过梯度上升优化网络参数 θ 以最大化下界。
3. 优化过程：通过对比真实数据分布 p(x,y) 与独立分布 p(x)p(y) 下的期望值，训练神经网络以逼近真实的互信息值。
主要定理与引理：
- 定理1：MINE方法通过优化Donsker-Varadhan下界，能够在理论上无限接近真实的互信息值。
- 引理1：在充分表达能力的神经网络和足够的训练样本下，MINE的估计具有一致性和无偏性。
具体结论：
MINE方法在高维复杂数据中的互信息估计效果显著优于传统方法，如K-NN估计和核密度估计。实验结果表明，MINE在多个任务中（如表示学习、生成模型训练）表现出色，能够有效捕捉数据中的复杂依赖关系，为高维数据的互信息分析提供了新的工具。
具体指导：
1. 表示学习：利用MINE估计互信息，可以设计新的损失函数，鼓励模型学习到更具信息量的特征表示。
2. 生成模型优化：在生成对抗网络（GANs）或变分自编码器（VAE）的训练中，引入MINE作为互信息的估计工具，优化生成器和判别器的协同训练。
3. 进一步研究方向：探索MINE在不同领域（如自然语言处理、计算机视觉）中的具体应用，以及其与其他信息估计方法的结合，提升互信息估计的效率和准确性。

6. 《Learning Diverse and Discriminative Representations via the Principle of Maximal Coding Rate Reduction (MCR²)》

中文标题：通过最大编码率减少原理学习多样且具辨别力的表示

背景与问题：
在表示学习中，优秀的特征表示不仅需要具备高辨别性（区分不同类别的能力），还应保持多样性（涵盖数据的丰富特征）。传统的监督学习方法往往侧重于提升辨别性，可能忽视特征的多样性，导致表示过于集中，缺乏泛化能力。
研究问题：
如何设计一种表示学习原则，能够同时最大化特征的多样性和辨别性，提升表示的质量和泛化能力？
提出的方法（MCR²原则）：
最大编码率减少（Maximal Coding Rate Reduction, MCR²）原则通过信息论中的编码率概念，定义表示学习目标如下：

其中，R(Z)是整体编码率，衡量表示 Z 的多样性；R(Z|C) 是类别条件下的编码率，衡量每个类别内部的冗余。具体实现步骤包括：
1. 编码率定义：利用高斯编码率公式，定义表示空间中的编码率： $R(Z) = \frac{1}{2} \log \det \left( I + \frac{d}{\epsilon^2} Z Z^T \right)$ 其中，d 是表示维度，ϵ 是噪声标准差。
2. 优化目标：设计损失函数，最大化编码率差异，即最大化整体编码率 R(Z) 与类别条件下编码率 R(Z|C) 之间的差异： $\mathcal{L} = R(Z|C) - R(Z)$ 通过最小化 $\mathcal{L}$ ，实现 $\Delta R$ 的最大化。
3. 网络训练：将MCR²目标融入神经网络的训练过程中，利用梯度下降优化网络参数，学习到既多样又具辨别力的特征表示。
主要定理与引理：
- 定理1：在给定的表示空间中，最大化 ΔR 能有效提升特征的多样性和辨别性，理论上可实现最佳的类间分离与类内聚集。
- 引理1：在高维表示空间中，编码率 R(Z) 与数据分布的复杂度成正比，能够反映数据的多样性。
- 引理2：类别条件下的编码率R(Z|C) 能有效衡量每个类别内部的冗余信息，最小化 R(Z|C) 有助于提升类别间的辨别能力。
具体结论：
MCR²方法在多个数据集和任务上表现出色，能够有效提升特征表示的多样性和辨别力。实验证明，MCR²在图像分类、语义分割等任务中相比传统方法具备更好的泛化能力和鲁棒性。此外，MCR²为表示学习提供了一个新的信息论基础，理论与实践相结合，验证了其在多样性与辨别性兼顾的特征学习中的有效性。
具体指导：
1. 表示学习框架：在设计表示学习模型时，引入MCR²原则，构建同时最大化多样性和辨别性的损失函数，提升特征表示质量。
2. 模型优化：通过优化编码率差异，指导模型参数更新，使得特征表示在类间具备良好的分离度，类内具备低冗余。
3. 进一步研究方向：探索MCR²在不同类型数据（如文本、音频）的应用，研究其与其他表示学习方法（如对比学习、生成模型）的结合，进一步提升特征表示的多样性与辨别力。

研讨纲要

1.信息论基础概念（10分钟）

1.1信源-信道-信宿模型

信息论由克劳德·香农（Claude Shannon）在20世纪中叶创立，主要研究信息的度量、存储、传输与处理。在机器学习和深度学习中，信息论提供了强有力的数学工具和理论框架，用于理解模型的学习机制、优化模型性能、进行特征选择以及提升模型的可解释性。以下是一个信源-信道-信宿模型：

信源是信息的起点，负责生成信息或数据。它可以是文本、图像、声音等各种形式的数据。
- 熵（平均自信息,比如抛掷一枚硬币的试验所包含的信息量）是衡量信息源不确定性的度量。信源熵越高，表示信源生成的信息越不确定、信息量越大。
  - 其他概念：自信息（某个消息出现的不确定性，也是这个消息所包含的信息量：I(x)=-logp(x),比如抛掷一枚硬币的结果是正面这个消息所包含的信息量）自信息量的单位与所用对数的底有关。
- 互信息衡量信源和信宿之间共享的信息量，即信源的信息对信宿的信息有多少帮助。
  - 平均互信息（一个事件集所给出关于另一个事件集的平均信息量，比如今天的天气所给出关于明天的天气的信息量）、平均条件互信息、平均联合互信息......
- 相对熵衡量两个概率分布之间的差异，常用于评估编码方案的效率。
- 信源编码（Source Coding）：常见方法有霍夫曼编码（Huffman Coding）、算术编码（Arithmetic Coding）等。目的：减少信息冗余，提高传输效率。
信道是信息传输的媒介，可以是物理介质（如电缆、光纤、空气中的无线电波）或抽象的传输路径（如互联网）。但在传输过程中可能会受到噪声、干扰等因素的影响，导致信息失真或丢失。
- 信道容量是信道在给定噪声条件下，能够无误差传输信息的最高速率。即每秒钟传输的最大比特数。对于二进制对称信道（Binary Symmetric Channel, BSC），信道容量 C 定义为 C=1−H(p) 其中 p 是信道错误概率，H(p) 是二进制熵函数。
- 香农证明，对于任何小于信道容量的传输速率，都存在一种编码方法，使得误码率可以任意小。
- 信道编码（Channel Coding）：常见方法有卷积码（Convolutional Codes）、块码（Block Codes）、涡轮码（Turbo Codes）等。目的：增加信息的冗余，抵抗信道噪声，提高传输的可靠性。
信宿是信息的接收端，负责接收并处理来自信源的信息。并将其还原或解码为可理解的形式。交叉熵可以为衡量接收端解码出的信息分布与发送端原始信息分布之间的差异，即传输过程中的信息失真或错误。

信息论不仅在理论上奠定了通信系统的基础，还在实际工程中有广泛的应用：

移动通信：如4G、5G网络中的编码与调制技术。
互联网：数据传输协议中的错误检测与纠正机制。
卫星通信：长距离传输中的信道编码技术。
存储设备：如硬盘、固态硬盘中的数据压缩与错误校正。

1.2信息论内容

熵（Entropy）：衡量随机变量不确定性的度量。对于一个离散随机变量 X，熵定义为：
$H(X)=-\sum_{x} p(x) \log p(x)$
熵越大，变量的不确定性越高。
条件熵（Conditional Entropy）：在给定另一个变量时剩余的不确定性。定义为：
$H(Y|X)=-\sum_{x,y} p(x,y) \log p(y|x)$
条件熵用于衡量在已知 X 的情况下，Y 的不确定性。
互信息（Mutual Information, MI）：衡量两个随机变量之间的依赖关系。定义为：
$I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X)$
当 X 与 Y 独立时，I(X;Y)=0。互信息在特征选择和表示学习中至关重要，因为它量化了一个变量中包含的关于另一个变量的信息量。
交叉熵（Cross Entropy）：衡量两个概率分布（通常是真实分布 p 与模型预测分布 q）之间差异的损失函数。定义为：
$H(p,q)= -\sum_{x} p(x) \log q(x)$
在分类任务中，交叉熵作为损失函数有助于模型快速收敛，优化模型预测的概率分布。
相对熵/KL散度（Kullback-Leibler Divergence, KL散度）：衡量两个概率分布 p 和 q 之间差异的非对称度量。定义为：
$D_{KL}(p \| q) = \sum_{x} p(x) \log \frac{p(x)}{q(x)}$
KL散度在变分推断、变分自编码器（VAE）等领域有重要应用，用于衡量近似分布与真实分布之间的差异。

1.3信息论在机器学习中的作用

1.3.1信源-信道-信宿模型架构的类比

在机器学习和深度学习中，整个数据处理过程可以类比为SCD模型：

信源（Source）：
- 类比：数据生成器，如数据集或数据分布。
- 作用：生成或提供用于训练和测试的原始数据。例如，在图像分类任务中，信源即是图像数据集。
信道（Channel）：
- 类比：数据预处理、特征提取、模型参数等中间处理步骤。
- 作用：将信源生成的数据转换为适合模型学习的形式。信道可能包括数据增强、特征变换、网络层的处理等。根据“互信息”“交叉熵”等概念选择对结果影响大的特征优化。噪声可以类比为模型的不确定性、数据的噪声。
```
criterion = nn.CrossEntropyLoss()
loss = criterion(y_pred, y_true)
loss.backward()
```
信宿（Destination）：
- 类比：模型的输出，如预测结果或生成的样本。
- 作用：接收并处理通过信道传输的数据，产生最终的输出结果。例如，分类器输出的类别标签。交叉熵损失函数用于衡量模型预测的类别概率分布与真实类别分布之间的差异。

1.3.2信息度量

熵（Entropy）：
- 在ML中的应用：熵用于衡量数据集的不确定性或多样性。例如，在决策树算法中，熵被用来选择最佳的分裂特征（信息增益）。
互信息（Mutual Information）：
- 在ML中的应用：互信息衡量两个变量之间共享的信息量，用于特征选择和特征提取。例如，在特征选择中，选择与目标变量具有高互信息的特征，以提高模型性能。
KL散度（Kullback-Leibler Divergence）：
- 在ML中的应用：KL散度用于衡量两个概率分布之间的差异，广泛应用于变分自编码器（Variational Autoencoders, VAEs）和生成对抗网络（Generative Adversarial Networks, GANs）的训练中。

1.4信息论在机器学习中的应用

1.4.1神经网络损失函数（分类）

在信息论的出现之前，神经网络的损失函数通常是基于传统的误差函数，如 均方误差（MSE，Mean Squared Error）、0-1损失（Zero-One Loss）、Hinge损失（Hinge Loss）。

均方误差（MSE）：对于回归任务，MSE是最常用的损失函数之一。它的计算方法是对网络预测值和真实值之间的差值进行平方，再求平均值：
- $MSE = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2$ 其中， $y_i$ 是实际标签， $\hat{y}_i$ 是预测值，N是样本数量。
- 不适应性：它假设输出是连续值，而分类问题的输出是离散的类别。
- 梯度消失：当预测值与真实值非常接近时，损失值很小，导致梯度非常小，这可能导致梯度消失，进而影响深层神经网络的训练效果。
0-1损失（Zero-One Loss）：0-1损失是一种简单的分类损失函数，通常用于判定分类任务的正确性。其损失值为0或1，表示模型是否预测正确。
- $\text{0-1 Loss} = \begin{cases} 0 & \text{if } y = \hat{y} \\ 1 & \text{if } y \neq \hat{y} \end{cases}$ 其中，y 是真实标签， $\hat{y}$ 是模型的预测标签。
- 0-1损失是一个不连续的函数，难以进行梯度下降优化，不利于模型的训练。由于它不能提供关于分类置信度的信息，因此在训练时无法进行平滑优化。它并不提供关于模型输出的概率信息，因此不适用于基于概率的优化方法。
Hinge损失（铰链损失）：最早在支持向量机（SVM）中使用。它主要用于二分类问题，目标是确保分类间隔最大化。
- $\text{Hinge Loss} = \sum_{i=1}^{N} \max(0, 1 - y_i \cdot \hat{y}_i)$ 其中， $y_i$ 是真实标签（取值为 $\pm1$ ）， $\hat{y}_i$ 是模型输出。
- Hinge损失需要将标签设置为±1，而不适用于原始的[0,1]标签。它没有概率输出，因此在需要概率输出的任务中不适用。

随着信息论的引入，尤其是 Kullback-Leibler散度（KL散度） 和 交叉熵 的应用，损失函数得到了显著的改进。信息论提供了一种新的视角，将损失函数与概率分布之间的距离联系起来，从而更好地衡量预测结果与实际分布之间的差异。

交叉熵与信息论的关系：交叉熵损失函数本质上是信息论中的一个重要概念，用来衡量真实分布与预测分布之间的差异。它可以被理解为衡量一个分布编码另一个分布的额外信息量。信息论中的 KL散度 量化了两个概率分布之间的差异，而交叉熵损失则是最小化这种差异的一种方法。
信息论的优势：
- 有效性：通过最小化KL散度或交叉熵，神经网络的输出概率分布和实际标签之间的差距被精确量化，这使得网络在分类任务中表现更加优越。
- 提高稳定性：信息论提供的度量方法有助于避免梯度消失问题，特别是在深度网络中，通过更加合理的损失函数，网络的训练可以更加稳定和快速。
- 更好的泛化性：交叉熵损失能够有效地引导网络优化，从而提高了模型的泛化能力，尤其是在处理具有多类标签的任务时。

在分类任务中，常使用交叉熵作为损失函数，以最小化模型预测分布 q(y|x) 与真实分布 p(y|x) 之间的差异。训练过程可以视为最小化KL散度 $D_{KL}(p \| q)$ ，从而使模型的预测更接近真实分布。

1.4.1.1代码

对比MSELoss和交叉熵的分类效果：

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_classification
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import adjusted_rand_score

# 1. 生成模拟数据
n_samples = 1000
X, y = make_classification(n_samples=n_samples, n_features=20, n_informative=10, n_clusters_per_class=2, random_state=42)

# 2. 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 将数据转换为PyTorch的tensor
X_tensor = torch.tensor(X_scaled, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.long)  # 确保标签是torch.long类型

# 3. 定义CrossE方法
class CrossEntropyModel(nn.Module):
    def __init__(self, input_dim, encoding_dim):
        super(CrossEntropyModel, self).__init__()
        # 编码器部分
        self.encoder = nn.Sequential(
            nn.Linear(input_dim, 64),
            nn.ReLU(),
            nn.Linear(64, encoding_dim)
        )
    
    def forward(self, x):
        encoded = self.encoder(x)
        return encoded

# 3. 定义MSELoss模型
class MSELossModel(nn.Module):
    def __init__(self, input_dim, encoding_dim):
        super(MSELossModel, self).__init__()
        # 编码器部分
        self.encoder = nn.Sequential(
            nn.Linear(input_dim, 64),
            nn.ReLU(),
            nn.Linear(64, encoding_dim)
        )

    def forward(self, x):
        encoded = self.encoder(x)
        return encoded

# 4. 定义自定义训练函数
def train_model(model, data, target, epochs=50, lr=0.01, method='autoencoder'):
    criterion = nn.MSELoss() if method == 'autoencoder' else nn.CrossEntropyLoss()
    optimizer = optim.Adam(model.parameters(), lr=lr)
    
    for epoch in range(epochs):
        model.train()
        optimizer.zero_grad()
        if method == 'autoencoder':
            encoded = model(data)
            target_one_hot = torch.nn.functional.one_hot(target, num_classes=encoded.shape[1]).float()
            loss = criterion(encoded, target_one_hot)  # 将标签转换为one-hot编码，MSE损失
        else:
            encoded = model(data)
            loss = criterion(encoded, target)  # CrossE方法的损失假设是交叉熵损失
        
        loss.backward()
        optimizer.step()
        if (epoch + 1) % 10 == 0:
            print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')

# 5. 聚类评估函数
def evaluate_with_kmeans(features, true_labels, n_clusters=2):
    kmeans = KMeans(n_clusters=n_clusters, random_state=42)
    kmeans.fit(features)
    predicted_labels = kmeans.labels_
    return adjusted_rand_score(true_labels, predicted_labels)

# 6. 实验：训练MSELoss和CrossE并评估
input_dim = X_tensor.shape[1]
encoding_dim = 2

# 训练MSELoss模型
mse_model = MSELossModel(input_dim, encoding_dim)
train_model(mse_model, X_tensor, y_tensor, epochs=50, method='autoencoder')
mse_encoded = mse_model(X_tensor).detach().numpy()
mse_score = evaluate_with_kmeans(mse_encoded, y)

# CrossE方法
CEn_model = CrossEntropyModel(input_dim, encoding_dim)
train_model(CEn_model, X_tensor, y_tensor, epochs=50, method='mcr2')
CEn_encoded = CEn_model(X_tensor).detach().numpy()
CEn_score = evaluate_with_kmeans(CEn_encoded, y)

# 输出结果
print(f'MSELoss ARI (MSELoss): {mse_score:.4f}')
print(f'CrossE ARI: {CEn_score:.4f}')

# 可视化
plt.figure(figsize=(10, 8))

# 1. MSELoss方法可视化
plt.subplot(1, 2, 1)
plt.scatter(mse_encoded[:, 0], mse_encoded[:, 1], c=y, cmap='viridis', alpha=0.7)
plt.title('MSELoss')
plt.xlabel('Component 1')
plt.ylabel('Component 2')

# 2. CrossE方法可视化
plt.subplot(1, 2, 2)
plt.scatter(CEn_encoded[:, 0], CEn_encoded[:, 1], c=y, cmap='viridis', alpha=0.7)
plt.title('CrossE Method')
plt.xlabel('Component 1')
plt.ylabel('Component 2')

plt.tight_layout()
plt.show()

首先，使用 make_classification 函数生成一个模拟的分类数据集，数据集有1000个样本，20个特征，其中有10个是信息性特征。数据标签 y 是二分类标签（0 或 1）。
然后，使用 StandardScaler 对数据进行标准化处理，使得每个特征的均值为0，方差为1，确保数据的尺度一致性。
CrossEntropyModel 和 MSELossModel 都是简单的神经网络模型。每个模型都有一个包含两个全连接层和一个ReLU激活函数的编码器部分。输出是一个表示数据编码的低维表示。
这两个模型在损失函数上有所不同：MSELossModel 使用均方误差损失（MSE），而 CrossEntropyModel 假设使用交叉熵损失（Cross-Entropy Loss），虽然在代码中交叉熵用于模型训练时的目标标签处理。
使用K-means算法对每个模型输出的低维编码进行聚类。然后，使用 调整兰德指数（Adjusted Rand Index，ARI） 来评估K-means聚类结果与真实标签之间的一致性。ARI的范围是[-1, 1]，值越大表示聚类结果与真实标签越一致。
- ARI（Adjusted Rand Index）是一个用于评估聚类算法结果的指标，常用来衡量聚类结果与真实标签的相似性。ARI的取值范围从 -1 到 1，其中：
  - 1 表示完美的聚类结果，即聚类标签完全与真实标签一致。
  - 0 表示聚类结果与真实标签无关，类似于随机聚类。
  - 负值表示聚类结果比随机聚类更差。

MSELoss ARI: 0.8873
CrossE ARI: 0.9761

1.4.2决策树

决策树算法（如ID3、C4.5）在构建树时通过计算信息增益（Information Gain）来选择最佳分裂特征。信息增益定义为：

$IG(Y|X) = H(Y) - H(Y|X)$

选择信息增益最大的特征作为分裂节点，能够最大化减少目标变量 Y 的不确定性，从而提高模型的分类性能。

1.4.2.1代码

import numpy as np
import pandas as pd

# 计算信息熵
def entropy(y):
    unique_classes, counts = np.unique(y, return_counts=True)
    prob = counts / len(y)
    return -np.sum(prob * np.log2(prob))

# 计算信息增益
def information_gain(X, y, feature_index):
    # 计算特征的所有取值
    feature_values = np.unique(X[:, feature_index])
    # 计算特征的条件熵
    weighted_entropy = 0
    for value in feature_values:
        subset_y = y[X[:, feature_index] == value]
        weighted_entropy += (len(subset_y) / len(y)) * entropy(subset_y)
    # 信息增益 = 总熵 - 条件熵
    return entropy(y) - weighted_entropy

# 找到具有最大信息增益的特征
def best_split(X, y):
    best_feature = None
    best_gain = -1
    for feature_index in range(X.shape[1]):
        gain = information_gain(X, y, feature_index)
        print(f'Feature {feature_index} Information Gain: {gain:.4f}')
        if gain > best_gain:
            best_gain = gain
            best_feature = feature_index
    return best_feature

# ID3决策树训练函数
class DecisionTreeID3:
    def __init__(self, max_depth=None):
        self.max_depth = max_depth
        self.tree = None

    def fit(self, X, y, depth=0):
        # 如果所有样本属于同一类别，或者没有特征可以继续划分
        if len(np.unique(y)) == 1:
            return np.unique(y)[0]

        if X.shape[1] == 0 or (self.max_depth is not None and depth == self.max_depth):
            return np.random.choice(np.unique(y))

        # 找到最优的特征进行划分
        best_feature = best_split(X, y)
        if best_feature is None:
            return np.random.choice(np.unique(y))

        # 根据最优特征划分数据
        tree = {}
        feature_values = np.unique(X[:, best_feature])
        for value in feature_values:
            subset_X = X[X[:, best_feature] == value]
            subset_y = y[X[:, best_feature] == value]
            subtree = self.fit(subset_X, subset_y, depth + 1)
            tree[value] = subtree

        return (best_feature, tree)

    def predict(self, X):
        return np.array([self._predict_single(sample) for sample in X])

    def _predict_single(self, sample):
        tree = self.tree
        while isinstance(tree, tuple):
            feature_index, subtree = tree
            feature_value = sample[feature_index]
            tree = subtree.get(feature_value, None)
            if tree is None:
                return None
        return tree

# 测试数据集：假设有一个简单的数据集
data = {
    'Outlook': ['Sunny', 'Sunny', 'Overcast', 'Rain', 'Rain', 'Rain', 'Overcast', 'Sunny', 'Sunny', 'Rain', 'Sunny', 'Overcast', 'Overcast', 'Rain'],
    'Temperature': ['Hot', 'Hot', 'Hot', 'Mild', 'Cool', 'Cool', 'Mild', 'Mild', 'Cool', 'Mild', 'Mild', 'Mild', 'Cool', 'Hot'],
    'Humidity': ['High', 'High', 'High', 'High', 'High', 'Normal', 'Normal', 'Normal', 'Normal', 'Normal', 'High', 'Normal', 'Normal', 'High'],
    'Wind': ['Weak', 'Strong', 'Weak', 'Weak', 'Weak', 'Weak', 'Weak', 'Weak', 'Weak', 'Strong', 'Weak', 'Strong', 'Strong', 'Weak'],
    'PlayTennis': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No']
}

df = pd.DataFrame(data)

# 将字符串特征转换为数字
df['Outlook'] = pd.Categorical(df['Outlook']).codes
df['Temperature'] = pd.Categorical(df['Temperature']).codes
df['Humidity'] = pd.Categorical(df['Humidity']).codes
df['Wind'] = pd.Categorical(df['Wind']).codes
df['PlayTennis'] = pd.Categorical(df['PlayTennis']).codes

X = df.drop('PlayTennis', axis=1).values
y = df['PlayTennis'].values

# 训练决策树
tree_model = DecisionTreeID3(max_depth=3)
tree_model.tree = tree_model.fit(X, y)

# 输出最终的决策树
print("Final Decision Tree:")
print(tree_model.tree)

# 使用模型进行预测
predictions = tree_model.predict(X)
print("\nPredictions:", predictions)

Feature 0 Information Gain: 0.2467
Feature 1 Information Gain: 0.1981
Feature 2 Information Gain: 0.0161
Feature 3 Information Gain: 0.0150
Feature 0 Information Gain: 0.0000
Feature 1 Information Gain: 0.5710
Feature 2 Information Gain: 0.0200
Feature 3 Information Gain: 0.1710
Feature 0 Information Gain: 0.0000
Feature 1 Information Gain: 0.0000
Feature 2 Information Gain: 1.0000
Feature 3 Information Gain: 0.0000
Feature 0 Information Gain: 0.0000
Feature 1 Information Gain: 0.5710
Feature 2 Information Gain: 0.0200
Feature 3 Information Gain: 0.1710
Feature 0 Information Gain: 0.0000
Feature 1 Information Gain: 0.0000
Feature 2 Information Gain: 1.0000
Feature 3 Information Gain: 0.0000
Final Decision Tree:
(0, {0: 1, 1: (1, {0: (2, {0: 1, 1: 0}), 1: 0, 2: 1}), 2: (1, {0: 1, 1: 0, 2: (2, {0: 1, 1: 0})})})

Predictions: [0 0 1 1 1 0 1 0 1 1 1 1 1 0]

除此之外，还有：

信息瓶颈（Information Bottleneck, IB）理论：
信息瓶颈方法通过在输入 X 和输出 Y 之间引入中间表示 Z，旨在最大化 I(Z;Y)（保留与标签相关的信息）同时最小化 I(Z; X)（去除与任务无关的信息），公式如下：
$\max_{p(z|x)} \left( I(Z; Y) - \beta I(Z; X) \right)$
其中，β 是权衡参数。IB理论用于理解和优化模型的表示学习过程，提升模型的泛化能力。
变分自编码器（VAE）和表示学习：
VAE通过最小化重构误差和KL散度来学习潜在变量的分布。目标函数包含了一个信息论项，用于确保潜在空间的结构良好，使得生成的数据与真实数据分布相匹配。
生成对抗网络（GANs）中的分布匹配：
GANs通过生成器和判别器的对抗训练，旨在最小化生成分布与真实数据分布之间的差异。信息论角度来看，这可以视为最小化某种信息差异，如Jensen-Shannon散度，从而优化生成过程。
神经网络的可解释性与层间信息流：
通过分析网络各层之间的互信息（如输入与隐藏层表示、隐藏层表示与输出之间的互信息），可以揭示模型的决策机制和内部工作原理，提升模型的可解释性。

2.编码原则（类比信源编码）（10分钟）

表示学习中的编码率减少原则《通过最大编码率减少原理学习多样且具辨别力的表示》

研究问题：如何同时最大化特征的多样性和辨别性？
方法：MCR²（Maximal Coding Rate Reduction）减少冗余信息，从而使得特征更加紧凑且具有更多区分性。基本思想：将样本特征的编码分布与目标类别之间的关系最大化，使得类别之间的表示差异最大化，减少类别内样本的相似性。
- 编码率定义（利用高斯编码率公式，定义表示空间中的编码率）： $R(Z) = \frac{1}{2} \log \det \left( I + \frac{d}{\epsilon^2} Z Z^T \right)$
- 类比已有信源编码方式：在我的另一篇blog中有详细介绍：《编码定理，霍夫曼Huffman编码、香农Shannon-Fano编码、算术编码、LZW字典编码、行程编码、预测编码、变换编码》在狭义相对论（即信道）中，从提高信息传输效率的观点出发，人们总是希望尽量去掉剩余度。信源编码是减少或消除信源的剩余度（冗余）以提高信息的传输效率。在机器学习任务中，同样可以对类比的“信源”做类似的操作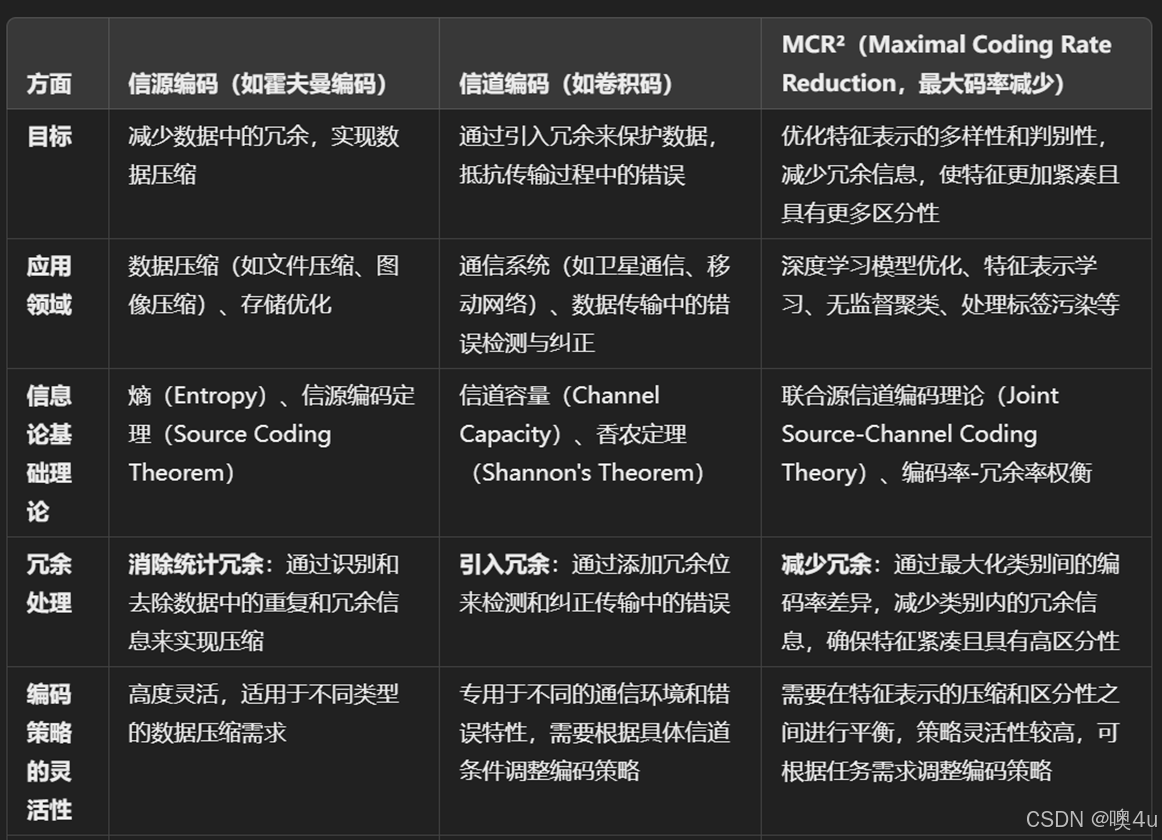：MCR²通过最大化整体编码率，鼓励特征表示具有更高的多样性，避免特征空间中出现冗余或重复的特征。最大编码率减少（MCR²）与霍夫曼编码、字典编码等源编码方法虽然在目标和应用领域上有所不同，但都基于信息论的基本原理，涉及信息的度量和编码策略。具体而言：
  - 源编码主要关注通过减少数据冗余，提高信息传输和存储的效率。
  - MCR²则侧重于通过优化特征表示的多样性和判别性，提升机器学习模型的分类性能和泛化能力。
- 优化目标： $\Delta R = R(Z) - R(Z|C)$
- 实现步骤：
  - 定义整体编码率 R(Z) 和类别条件下编码率 R(Z|C)。
  - 设计损失函数 $\mathcal{L} = R(Z|C) - R(Z)$ 。
  - 通过梯度下降优化网络参数，最大化编码率差异。
- 基本思想
  - 将样本特征的编码分布与目标类别之间的关系最大化，使得类别之间的表示差异最大化，减少类别内样本的相似性。
    - Between-Class Discriminative：不同类别/簇的样本特征应该是高度不相关的，并且属于不同的低维线性子空间。
    - Within-Class Compressible：同一类别/簇的样本特征应该是相对相关的，意味着它们属于一个低维线性子空间。
    - Maximally Diverse Representation：每个类别/簇的特征维度（或方差）应该尽可能大，只要它们保持与其它类别不相关。
  - 目标：学习一个映射，将高维数据（位于低维流形上）映射到低维子空间，并满足上述三个属性。这种方法不仅在理论上保证了在收敛时期望的属性，而且在实践中具有鲁棒性，能够处理标签污染等问题，并在无监督聚类性能上取得了最先进的结果。
主要定理：
- 定理1：最大化 $\Delta R$ 提升特征的多样性和辨别性。
- 引理1：高维表示空间中，编码率与数据分布复杂度成正比。
- 引理2：类别条件下的编码率有效衡量类内冗余，最小化 R(Z|C) 提升辨别能力。
  - 图(a)：随着迭代次数增加，ΔR（绿线）稳步增长，说明特征表示的区分性在增强。
    
    图(b): 对比训练和测试的损失变化，训练和测试的 R 和 Δ 均逐步趋于稳定。
    
    图(c): 使用PCA分析特征，红色表示全局数据的特征变化，蓝色表示每个类别的特征分布。可以看出类别特征在PCA空间中有良好的分布。
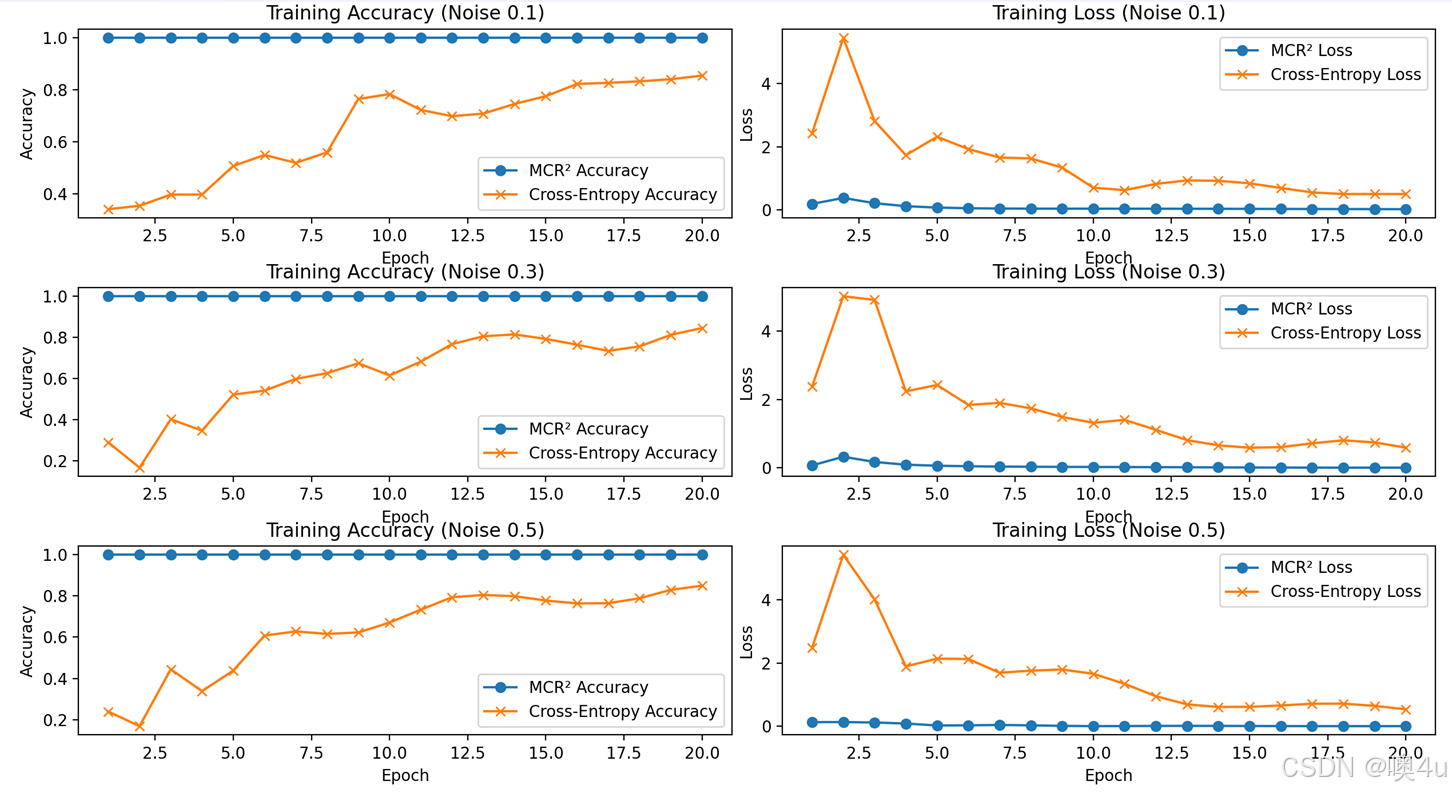
  - (a): 研究了不同噪声水平对 ΔR 的影响。噪声越大，训练的收敛速度越慢，但最终仍能趋于稳定。
    
    (b): 对比不同噪声水平下的 R，噪声越高，收敛的编码率略低。
    
    (c): 类条件编码率 Rc 随噪声增加而逐渐增大，说明噪声对类内特征的压缩性有负面影响。
结论：MCR²在多个数据集和任务中表现优异，提升了特征的多样性和辨别力。
- MCR可以视为在优化过程中间接最小化了一种“散度”——即优化特征空间中类内与类间的差异，而这种差异可以通过KL散度来量化。KL散度反映了类别之间的分布差异，MCR损失在某种程度上可以被看作是在最小化类别之间的KL散度。
具体指导：
- 在表示学习模型中引入MCR²原则，优化特征表示的多样性与辨别性。
- 利用编码率差异指导模型参数更新，实现类间分离和类内聚集。
- 探索MCR²在不同数据类型和与其他方法的结合应用。
2.1MCR²代码展示

以监督学习为例，原文使用的是CIFAR10 数据集 ResNet-18架构，为了减小计算量，我用mnist和一个简单的简单的线性映射模型，定义维度为2，噪声标准差为1*10-4. 这就是训练结果，可以看到不论是从模型拟合的速度还是准确率， mcr方损失函数在mnist这样简单的数据集上都优于交叉熵损失函数的模型。

import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.metrics import accuracy_score
from torchvision import datasets, transforms
import matplotlib.pyplot as plt

# 加载MNIST数据集

def load_mnist_data(noise_level=0.0):
    transform = transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.5,), (0.5,)),
        lambda x: x + noise_level * torch.randn_like(x)  # 添加噪声
    ])
    train_dataset = datasets.MNIST(root=r'.\mnist', train=True, transform=transform, download=False)
    train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=1000, shuffle=True)
    return next(iter(train_loader))

# 定义简单的线性映射模型
class LinearMapping(nn.Module):
    def __init__(self, input_dim, output_dim):
        super(LinearMapping, self).__init__()
        self.linear = nn.Linear(input_dim, output_dim, bias=False)

    def forward(self, x):
        return self.linear(x)

# 定义 MCR² 损失函数
def mcr2_loss(Z, y, epsilon=1e-5):
    n, d = Z.size()
    R = 0.5 * torch.logdet(torch.eye(d) + (1 / (n * epsilon ** 2)) * Z.T @ Z)

    Rc = 0
    for cls in torch.unique(y):
        Z_cls = Z[y == cls]
        n_cls = Z_cls.size(0)
        Rc += 0.5 * (n_cls / n) * torch.logdet(
            torch.eye(d) + (1 / (n_cls * epsilon ** 2)) * Z_cls.T @ Z_cls
        )

    return R - Rc

# 设置不同噪声水平
noise_levels = [0.1, 0.3, 0.5]
results = {}

for noise_level in noise_levels:
    print(f"Training with noise level: {noise_level}")

    # 加载数据
    X, y = load_mnist_data(noise_level=noise_level)
    X = X.view(X.size(0), -1)  # 展平数据

    latent_dim = 2
    num_classes = 10

    # 初始化模型
    model_mcr2 = LinearMapping(input_dim=X.size(1), output_dim=latent_dim)
    optimizer_mcr2 = optim.Adam(model_mcr2.parameters(), lr=0.01)

    model_ce = nn.Linear(X.size(1), num_classes, bias=False)
    optimizer_ce = optim.Adam(model_ce.parameters(), lr=0.01)
    criterion_ce = nn.CrossEntropyLoss()

    # 初始化用于可视化的指标
    mcr2_train_acc = []
    mcr2_train_loss = []
    ce_train_acc = []
    ce_train_loss = []

    # 训练模型 (MCR²)
    epochs = 20
    for epoch in range(epochs):
        # MCR²
        model_mcr2.train()
        optimizer_mcr2.zero_grad()

        Z = model_mcr2(X)
        loss = mcr2_loss(Z, y)

        loss.backward()
        optimizer_mcr2.step()

        # 记录训练损失和准确率
        with torch.no_grad():
            Z_eval = model_mcr2(X)
            Z_eval = Z_eval.numpy()
            y_pred = []
            for i, z in enumerate(Z_eval):
                distances = np.linalg.norm(Z_eval - z, axis=1)
                nearest_idx = np.argmin(distances)
                y_pred.append(y[nearest_idx].item())
            acc = accuracy_score(y.numpy(), y_pred)
            mcr2_train_acc.append(acc)
            mcr2_train_loss.append(loss.item())

        # Cross-Entropy
        model_ce.train()
        optimizer_ce.zero_grad()

        logits = model_ce(X)
        loss = criterion_ce(logits, y)

        loss.backward()
        optimizer_ce.step()

        # 记录训练损失和准确率
        with torch.no_grad():
            logits_eval = model_ce(X)
            y_pred_ce = torch.argmax(logits_eval, dim=1).numpy()
            acc_ce = accuracy_score(y.numpy(), y_pred_ce)
            ce_train_acc.append(acc_ce)
            ce_train_loss.append(loss.item())

    # 存储结果
    results[noise_level] = {
        "mcr2_train_acc": mcr2_train_acc,
        "mcr2_train_loss": mcr2_train_loss,
        "ce_train_acc": ce_train_acc,
        "ce_train_loss": ce_train_loss
    }

# 绘制训练过程的准确率和损失
plt.figure(figsize=(12, 12))

for i, noise_level in enumerate(noise_levels):
    result = results[noise_level]

    # 绘制训练准确率
    plt.subplot(len(noise_levels), 2, 2 * i + 1)
    plt.plot(range(1, epochs + 1), result["mcr2_train_acc"], label="MCR² Accuracy", marker='o')
    plt.plot(range(1, epochs + 1), result["ce_train_acc"], label="Cross-Entropy Accuracy", marker='x')
    plt.title(f"Training Accuracy (Noise {noise_level})")
    plt.xlabel("Epoch")
    plt.ylabel("Accuracy")
    plt.legend()

    # 绘制训练损失
    plt.subplot(len(noise_levels), 2, 2 * i + 2)
    plt.plot(range(1, epochs + 1), result["mcr2_train_loss"], label="MCR² Loss", marker='o')
    plt.plot(range(1, epochs + 1), result["ce_train_loss"], label="Cross-Entropy Loss", marker='x')
    plt.title(f"Training Loss (Noise {noise_level})")
    plt.xlabel("Epoch")
    plt.ylabel("Loss")
    plt.legend()

plt.tight_layout()
plt.show()

2.2MCR²代码展示(非原文，结合其他损失函数)

结果：仍优

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
import numpy as np
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 设置随机种子以确保结果可重复
torch.manual_seed(42)
np.random.seed(42)

# 检查设备
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f'使用设备: {device}')

# 1. 定义MCR²损失函数
class MCR2Loss(nn.Module):
    def __init__(self, feature_dim, num_classes, epsilon=1e-4):
        super(MCR2Loss, self).__init__()
        self.feature_dim = feature_dim
        self.num_classes = num_classes
        self.epsilon = epsilon  # 防止数值不稳定

    def forward(self, Z, labels):
        """
        Z: 特征表示 [batch_size, feature_dim]
        labels: 标签 [batch_size]
        """
        batch_size, feature_dim = Z.size()

        # 归一化特征
        Z_norm = Z / (torch.norm(Z, dim=1, keepdim=True) + self.epsilon)

        # 计算整体编码率 R(Z)
        covariance = torch.matmul(Z_norm.T, Z_norm) / batch_size + self.epsilon * torch.eye(feature_dim).to(Z.device)
        try:
            _, logdet = torch.slogdet(covariance)
            R_Z = 0.5 * logdet
        except RuntimeError:
            R_Z = torch.tensor(0.0, device=Z.device)

        # 计算类别条件下的编码率 R(Z|C)
        R_ZC = 0.0
        for c in range(self.num_classes):
            mask = (labels == c)
            Z_c = Z_norm[mask]
            if Z_c.size(0) == 0:
                continue
            batch_c, _ = Z_c.size()
            covariance_c = torch.matmul(Z_c.T, Z_c) / batch_c + self.epsilon * torch.eye(feature_dim).to(Z.device)
            try:
                _, logdet_c = torch.slogdet(covariance_c)
                R_ZC += 0.5 * logdet_c
            except RuntimeError:
                R_ZC += torch.tensor(0.0, device=Z.device)

        R_ZC = R_ZC / self.num_classes

        # MCR²损失，归一化
        loss = (R_ZC - R_Z) / self.feature_dim
        return loss

# 2. 定义神经网络模型
class SimpleNet(nn.Module):
    def __init__(self, input_dim=28*28, feature_dim=64, num_classes=10):
        super(SimpleNet, self).__init__()
        self.feature_extractor = nn.Sequential(
            nn.Linear(input_dim, 256),
            nn.ReLU(),
            nn.Linear(256, feature_dim),
            nn.ReLU()
        )
        self.classifier = nn.Linear(feature_dim, num_classes)

    def forward(self, x):
        x = x.view(x.size(0), -1)  # 展平
        features = self.feature_extractor(x)
        logits = self.classifier(features)
        return features, logits

# 3. 准备数据集
def get_data_loaders(batch_size=128):
    # 数据预处理
    transform = transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))  # MNIST的均值和标准差
    ])

    # 下载MNIST数据集
    train_dataset = datasets.MNIST(root='./mnist', train=True, transform=transform, download=False)
    test_dataset = datasets.MNIST(root='./mnist', train=False, transform=transform, download=False)

    # 数据加载器
    train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
    test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)

    return train_loader, test_loader

# 4. 定义训练函数
def train(model, device, train_loader, optimizer, ce_loss_fn, mcr2_loss_fn=None, alpha=1.0):
    model.train()
    total_loss = 0.0
    total_ce_loss = 0.0
    total_mcr2_loss = 0.0
    correct = 0
    total = 0

    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)

        optimizer.zero_grad()
        features, logits = model(data)

        ce_loss = ce_loss_fn(logits, target)
        if mcr2_loss_fn is not None:
            mcr2_loss = mcr2_loss_fn(features, target)
            loss = ce_loss + alpha * mcr2_loss
        else:
            loss = ce_loss

        loss.backward()
        optimizer.step()

        total_loss += loss.item()
        total_ce_loss += ce_loss.item()
        if mcr2_loss_fn is not None:
            total_mcr2_loss += mcr2_loss.item()

        # 计算准确率
        _, predicted = torch.max(logits.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()

    avg_loss = total_loss / len(train_loader)
    avg_ce_loss = total_ce_loss / len(train_loader)
    avg_mcr2_loss = total_mcr2_loss / len(train_loader) if mcr2_loss_fn is not None else 0.0
    accuracy = 100.0 * correct / total

    return avg_loss, avg_ce_loss, avg_mcr2_loss, accuracy

def train_combined(model, device, train_loader, optimizer, ce_loss_fn, mcr2_loss_fn, alpha=0.1):
    model.train()
    total_loss = 0.0
    total_ce_loss = 0.0
    total_mcr2_loss = 0.0
    correct = 0
    total = 0

    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)

        optimizer.zero_grad()
        features, logits = model(data)

        ce_loss = ce_loss_fn(logits, target)
        mcr2_loss = mcr2_loss_fn(features, target)
        loss = ce_loss + alpha * mcr2_loss

        loss.backward()
        optimizer.step()

        total_loss += loss.item()
        total_ce_loss += ce_loss.item()
        total_mcr2_loss += mcr2_loss.item()

        # 计算准确率
        _, predicted = torch.max(logits.data, 1)
        total += target.size(0)
        correct += (predicted == target).sum().item()

    avg_loss = total_loss / len(train_loader)
    avg_ce_loss = total_ce_loss / len(train_loader)
    avg_mcr2_loss = total_mcr2_loss / len(train_loader)
    accuracy = 100.0 * correct / total

    return avg_loss, avg_ce_loss, avg_mcr2_loss, accuracy


# 5. 定义测试函数
def test(model, device, test_loader, ce_loss_fn):
    model.eval()
    test_loss = 0.0
    correct = 0
    total = 0

    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            features, logits = model(data)
            ce_loss = ce_loss_fn(logits, target)
            test_loss += ce_loss.item()

            _, predicted = torch.max(logits.data, 1)
            total += target.size(0)
            correct += (predicted == target).sum().item()

    avg_loss = test_loss / len(test_loader)
    accuracy = 100.0 * correct / total

    return avg_loss, accuracy

# 6. 可视化特征表示
def visualize_features(model, device, test_loader, num_samples=1000, title='t-SNE of Feature Representations'):
    model.eval()
    features_list = []
    labels_list = []

    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            features, logits = model(data)
            features_list.append(features.cpu().numpy())
            labels_list.append(target.cpu().numpy())
            if len(features_list) * data.size(0) >= num_samples:
                break

    features = np.concatenate(features_list, axis=0)[:num_samples]
    labels = np.concatenate(labels_list, axis=0)[:num_samples]

    # 使用t-SNE进行降维
    tsne = TSNE(n_components=2, random_state=42)
    features_tsne = tsne.fit_transform(features)

    # 绘制结果
    plt.figure(figsize=(8, 6))
    scatter = plt.scatter(features_tsne[:, 0], features_tsne[:, 1], c=labels, cmap='tab10', alpha=0.7)
    plt.legend(*scatter.legend_elements(), title="Classes")
    plt.title(title)
    plt.xlabel('Dimension 1')
    plt.ylabel('Dimension 2')
    plt.show()

# 7. 主函数
def main():
    # 超参数
    batch_size = 128
    learning_rate = 1e-3
    num_epochs = 8
    feature_dim = 64
    num_classes = 10
    alpha = 0.1  # MCR²损失的权重

    # 获取数据加载器
    train_loader, test_loader = get_data_loaders(batch_size=batch_size)

    # 初始化模型A（仅使用交叉熵损失）
    model_A = SimpleNet(input_dim=28*28, feature_dim=feature_dim, num_classes=num_classes).to(device)
    ce_loss_fn = nn.CrossEntropyLoss()
    optimizer_A = optim.Adam(model_A.parameters(), lr=learning_rate)

    # 初始化模型B（结合使用交叉熵和MCR²损失）
    model_B = SimpleNet(input_dim=28*28, feature_dim=feature_dim, num_classes=num_classes).to(device)
    mcr2_loss_fn = MCR2Loss(feature_dim=feature_dim, num_classes=num_classes)
    optimizer_B = optim.Adam(model_B.parameters(), lr=learning_rate)

    # 记录训练和测试的损失与准确率
    train_losses_A = []
    train_accuracies_A = []
    test_losses_A = []
    test_accuracies_A = []

    train_losses_B = []
    train_accuracies_B = []
    test_losses_B = []
    test_accuracies_B = []

    # 训练与测试循环
    for epoch in range(1, num_epochs + 1):
        # 模型A：仅使用交叉熵损失
        train_loss_A, train_ce_A, _, train_acc_A = train(model_A, device, train_loader, optimizer_A, ce_loss_fn)
        test_loss_A, test_acc_A = test(model_A, device, test_loader, ce_loss_fn)

        train_losses_A.append(train_loss_A)
        train_accuracies_A.append(train_acc_A)
        test_losses_A.append(test_loss_A)
        test_accuracies_A.append(test_acc_A)

        print(f'模型A（仅交叉熵） - Epoch {epoch}/{num_epochs}:')
        print(f'  Train Loss: {train_loss_A:.4f} | Accuracy: {train_acc_A:.2f}%')
        print(f'  Test Loss: {test_loss_A:.4f} | Accuracy: {test_acc_A:.2f}%\n')

        # 模型B：结合使用交叉熵和MCR²损失
        train_loss_B, train_ce_B, train_mcr2_B, train_acc_B = train_combined(model_B, device, train_loader, optimizer_B, ce_loss_fn, mcr2_loss_fn, alpha)
        test_loss_B, test_acc_B = test(model_B, device, test_loader, ce_loss_fn)

        train_losses_B.append(train_loss_B)
        train_accuracies_B.append(train_acc_B)
        test_losses_B.append(test_loss_B)
        test_accuracies_B.append(test_acc_B)

        print(f'模型B（交叉熵 + MCR²） - Epoch {epoch}/{num_epochs}:')
        print(f'  Train Loss: {train_loss_B:.4f} | CE Loss: {train_ce_B:.4f} | MCR² Loss: {train_mcr2_B:.4f} | Accuracy: {train_acc_B:.2f}%')
        print(f'  Test Loss: {test_loss_B:.4f} | Accuracy: {test_acc_B:.2f}%\n')

    # 可视化训练和测试准确率
    plt.figure(figsize=(12, 5))

    plt.subplot(1, 2, 1)
    plt.plot(range(1, num_epochs + 1), train_accuracies_A, label='模型A - 训练准确率')
    plt.plot(range(1, num_epochs + 1), test_accuracies_A, label='模型A - 测试准确率')
    plt.plot(range(1, num_epochs + 1), train_accuracies_B, label='模型B - 训练准确率')
    plt.plot(range(1, num_epochs + 1), test_accuracies_B, label='模型B - 测试准确率')
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy (%)')
    plt.title('训练与测试准确率对比')
    plt.legend()
    plt.grid(True)

    # 可视化特征表示
    visualize_features(model_A, device, test_loader, num_samples=1000, title='模型A（仅交叉熵）的特征t-SNE')
    visualize_features(model_B, device, test_loader, num_samples=1000, title='模型B（交叉熵 + MCR²）的特征t-SNE')

    plt.show()

    # 打印最终测试准确率
    print(f'最终测试准确率 - 模型A（仅交叉熵）：{test_accuracies_A[-1]:.2f}%')
    print(f'最终测试准确率 - 模型B（交叉熵 + MCR²）：{test_accuracies_B[-1]:.2f}%')

if __name__ == '__main__':
    main()

20个epoch后：
最终测试准确率 - 模型A（仅交叉熵）：97.93%
最终测试准确率 - 模型B（交叉熵 + MCR²）：98.17%

可以看到加入了 MCR²后，模型拟合的质量和速度都有所提升。

3.互信息估计方法（5分钟）

互信息是衡量两个随机变量之间的依赖关系的度量，它反映了一个变量给定另一个变量时，能够提供多少信息。互信息的值越大，表示两个变量之间的依赖关系越强。特别地，如果 X 和 Y 完全相关，互信息会达到它们的熵值；如果它们是独立的，互信息则为零。

如果特征 X1 与目标标签 Y 之间的互信息 I(X1;Y) 很高，意味着 X1 对预测 Y 很有帮助。
如果特征 X2 与目标标签 Y 之间的互信息很低，意味着 X2 对预测 Y 并没有提供很多有价值的信息，甚至可以去除。

在深度学习中，互信息可以帮助我们选择最具代表性的特征。通过最大化输入数据与模型输出之间的互信息，可以学习到更有意义的表征（表示）。例如，在无监督学习中，通过最大化输入和模型隐层表示之间的互信息，可以获得更有效的特征表示。信息最大化策略通常被用于生成对抗网络（GAN）和变分自编码器（VAE）等模型中。

通过最小化输入数据与模型输出之间的冗余信息（即最小化不必要的部分），可以提高模型的泛化能力。深度学习中的一些损失函数，如对比损失（contrastive loss），尝试最大化正样本对之间的互信息，同时最小化负样本对之间的互信息，从而使得模型学习到有效的分离性特征。

MCR通过最大化类别间的分离度来提升聚类效果，而互信息直接度量了输入与输出之间的依赖关系。MCR与互信息之间的关系可以通过特征表示来体现，MCR会影响特征的表达能力，进而影响输入特征和标签之间的互信息。因此，MCR方法可以看作是在一定程度上最大化特征与标签之间的互信息。

《互信息的神经估计》

研究问题：如何在高维复杂数据中有效估计互信息。
方法：MINE（Mutual Information Neural Estimation）
- Donsker-Varadhan 表示： $I(X; Y) \geq \sup_{f \in \mathcal{F}} \mathbb{E}_{p(x,y)}[f(x,y)] - \log(\mathbb{E}_{p(x)p(y)}[e^{f(x,y)}])$
- 神经网络参数化：使用神经网络 $f_\theta(x, y)$ 进行互信息下界估计。
- 优化过程：通过梯度上升最大化下界，逼近真实互信息。
主要定理：
- 定理1：MINE通过优化下界，理论上能无限接近真实互信息。
- 引理1：在充分表达能力和足够训练样本下，MINE估计一致且无偏。
结论：MINE在高维数据中的互信息估计优于传统方法，适用于表示学习和生成模型。
- 展示实验结果，说明MINE在高维数据中的优势。

3.1代码展示

import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt
from matplotlib import cm
from sklearn.manifold import TSNE

# MINE相关导入
import torch.optim as optim
import torch.nn.functional as F

# 参数设置
EPOCH = 5
BATCH_SIZE = 128
LR = 0.001
DOWNLOAD_MNIST = False

# 下载MNIST数据集
train_data = torchvision.datasets.MNIST(
    root="./mnist",
    train=True,
    transform=torchvision.transforms.ToTensor(),
    download=DOWNLOAD_MNIST
)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)

test_data = torchvision.datasets.MNIST(
    root="./mnist",
    train=False
)
test_x = torch.unsqueeze(test_data.data, dim=1).type(torch.float32)[:2000] / 255.
test_y = test_data.targets[:2000]

# 定义CNN模型
class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(  
            nn.Conv2d(1, 16, 5, 1, 2),  
            nn.ReLU(),
            nn.MaxPool2d(2),
        )
        self.conv2 = nn.Sequential(  
            nn.Conv2d(16, 32, 5, 1, 2),  
            nn.ReLU(),
            nn.MaxPool2d(2),
        )
        self.out = nn.Linear(32 * 7 * 7, 10)  
    
    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)  
        self.features = x.view(x.size(0), -1)  # 保存中间特征
        output = self.out(self.features)
        return output

# 定义MINE网络
class MINE(nn.Module):
    def __init__(self, input_size, hidden_size=128):
        super(MINE, self).__init__()
        self.fc1 = nn.Linear(input_size, hidden_size)
        self.fc2 = nn.Linear(hidden_size, 1)
    
    def forward(self, x, y):
        combined = torch.cat([x, y], dim=1)
        h = F.relu(self.fc1(combined))
        output = self.fc2(h)
        return output

# 初始化模型、优化器和损失函数
cnn = CNN()
optimizer = optim.Adam(cnn.parameters(), lr=LR)
loss_func = nn.CrossEntropyLoss()

# 初始化MINE
mine = MINE(input_size=32*7*7 + 10)  # 输入为CNN的特征 + 输出
mine_optimizer = optim.Adam(mine.parameters(), lr=LR)

# 定义用于TSNE可视化的函数
def plot_with_labels(lowDWeights, labels, ax):
    ax.cla()
    X, Y = lowDWeights[:, 0], lowDWeights[:, 1]
    for x, y, s in zip(X, Y, labels):
        c = cm.rainbow(int(255 * s / 9))
        ax.text(x, y, s, backgroundcolor=c, fontsize=9)
    ax.set_xlim(X.min(), X.max())
    ax.set_ylim(Y.min(), Y.max())
    ax.set_title('Visualize last layer')
    ax.axis('off')
    plt.pause(0.01)

# 初始化可视化
plt.ion()
fig, (ax_tsne, ax_mi) = plt.subplots(1, 2, figsize=(12, 5))
mi_values = []
accuracy_values = []

for epoch in range(EPOCH):
    for step, (x, y) in enumerate(train_loader):
        # 训练CNN
        out = cnn(x)
        loss = loss_func(out, y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        # 估计互信息
        features = cnn.features.detach()
        outputs = F.softmax(out.detach(), dim=1)
        
        # 正样本
        joint = mine(features, outputs)
        # 负样本
        marg = mine(features, outputs[torch.randperm(outputs.size(0))])
        
        # MINE的损失函数
        mine_loss = -torch.mean(joint) + torch.log(torch.mean(torch.exp(marg)))
        
        # 训练MINE
        mine_optimizer.zero_grad()
        mine_loss.backward()
        mine_optimizer.step()

        if step % 100 == 0:
            # 计算准确率
            test_output = cnn(test_x)
            pred_y = torch.max(test_output, 1)[1].data.numpy()
            accuracy = float((pred_y == test_y.data.numpy()).astype(int).sum()) / float(test_y.size(0))
            print('Epoch: ', epoch, '| step: ', step, '| train loss: %.4f' % loss.data.numpy(), '| test accuracy: %.2f' % accuracy)
            
            # 记录互信息
            mi = torch.mean(joint - torch.log(torch.mean(torch.exp(marg)))).item()
            mi_values.append(mi)
            accuracy_values.append(accuracy)

            # 绘制互信息和准确率
            ax_mi.cla()
            ax_mi.plot(mi_values, label='Mutual Information')
            ax_mi.plot(accuracy_values, label='Test Accuracy')
            ax_mi.legend()
            ax_mi.set_xlabel('Steps (x100)')
            ax_mi.set_ylabel('Value')
            ax_mi.set_title('Mutual Information & Test Accuracy')
            
            # 绘制TSNE可视化
            tsne = TSNE(perplexity=30, n_components=2, init='pca', max_iter=5000)
            plot_only = 500
            low_dim_embs = tsne.fit_transform(test_output.data.numpy()[:plot_only, :])
            labels = test_y.numpy()[:plot_only]
            plot_with_labels(low_dim_embs, labels, ax_tsne)

plt.ioff()
plt.show()

# 测试模型
test_output = cnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')

MINE网络定义：
- MINE类是一个简单的神经网络，用于估计两个变量之间的互信息。它接受CNN的中间特征和输出概率作为输入，输出一个标量。
互信息估计与训练：
- 在每个训练步骤中，我们提取CNN的中间特征（features）和输出概率（outputs）。
- 正样本对是特征与正确的输出，负样本对是特征与随机打乱的输出。
- MINE的损失函数基于Donsker-Varadhan表示，用于最大化正样本的互信息下界，同时最小化负样本的影响。
  - 对CNN的中间特征和分类结果（softmax后的输出）计算互信息。
  - MINE损失：MINE的目标是最小化其损失函数，最大化特征和标签之间的互信息。
  - 负样本：通过MINE网络计算随机排序后的标签与特征的联合概率分布。
  - 正样本：通过MINE网络计算特征和标签的联合概率分布。
- 通过优化MINE网络，逼近实际的互信息值。
可视化互信息与准确率：
- 使用matplotlib的plt.subplots创建一个包含两个子图的图形窗口。
- 在左侧子图（ax_tsne）中展示CNN最后一层的TSNE可视化。
- 在右侧子图（ax_mi）中实时绘制互信息和测试准确率的变化。
- 使用plt.ion()实现实时绘图。

训练与测试：

Epoch:  0 | step:  0 | train loss: 2.3096 | test accuracy: 0.18
Epoch:  0 | step:  100 | train loss: 0.3091 | test accuracy: 0.91
Epoch:  0 | step:  200 | train loss: 0.1016 | test accuracy: 0.94
Epoch:  0 | step:  300 | train loss: 0.0901 | test accuracy: 0.96
Epoch:  0 | step:  400 | train loss: 0.0468 | test accuracy: 0.97
Epoch:  1 | step:  0 | train loss: 0.0817 | test accuracy: 0.97
Epoch:  1 | step:  100 | train loss: 0.0301 | test accuracy: 0.97
Epoch:  1 | step:  200 | train loss: 0.1281 | test accuracy: 0.98
Epoch:  1 | step:  300 | train loss: 0.0200 | test accuracy: 0.97
Epoch:  1 | step:  400 | train loss: 0.0748 | test accuracy: 0.98
Epoch:  2 | step:  0 | train loss: 0.0877 | test accuracy: 0.98
Epoch:  2 | step:  100 | train loss: 0.0587 | test accuracy: 0.98
Epoch:  2 | step:  200 | train loss: 0.0874 | test accuracy: 0.98
Epoch:  2 | step:  300 | train loss: 0.0343 | test accuracy: 0.98
Epoch:  2 | step:  400 | train loss: 0.0521 | test accuracy: 0.98
Epoch:  3 | step:  0 | train loss: 0.0564 | test accuracy: 0.98
Epoch:  3 | step:  100 | train loss: 0.0797 | test accuracy: 0.98
Epoch:  3 | step:  200 | train loss: 0.0745 | test accuracy: 0.98
Epoch:  3 | step:  300 | train loss: 0.0185 | test accuracy: 0.98
Epoch:  3 | step:  400 | train loss: 0.0283 | test accuracy: 0.98
Epoch:  4 | step:  0 | train loss: 0.0203 | test accuracy: 0.98
Epoch:  4 | step:  100 | train loss: 0.0498 | test accuracy: 0.98
Epoch:  4 | step:  200 | train loss: 0.0180 | test accuracy: 0.98
Epoch:  4 | step:  300 | train loss: 0.0074 | test accuracy: 0.98
Epoch:  4 | step:  400 | train loss: 0.0145 | test accuracy: 0.98

CNN和MINE网络同步训练，CNN负责分类任务，MINE负责互信息估计。
最终，展示前10个测试样本的预测结果与真实标签。

左侧子图：TSNE可视化
- 显示CNN最后一层特征的降维可视化。
- 不同颜色代表不同的数字类别。
- 通过观察TSNE图，可以直观地看到不同类别在特征空间中的分布情况。
右侧子图：互信息与准确率
- 互信息（Mutual Information）：随着训练的进行，互信息可能先上升后下降，反映了信息瓶颈理论中的“拟合阶段”和“压缩阶段”。
- 测试准确率（Test Accuracy）：随着训练的进行，准确率逐步提高，显示模型性能的提升。

进一步的讨论点

MINE的优势与局限：
- 优势：能够在高维数据中有效估计互信息，适用于复杂模型。
- 局限：需要额外的计算资源，训练MINE网络可能带来额外的优化挑战。
信息瓶颈理论的扩展：
- 如何将信息瓶颈理论应用于更复杂的任务（如自然语言处理、图像生成）。
- 与其他理论框架的结合，如统计学习理论、对比学习等。
实际应用中的优化策略：
- 如何更高效地集成互信息估计方法，减少训练时间。
- 通过互信息引导模型设计，提升模型的可解释性和泛化能力。

4.信息瓶颈理论在深度学习中的应用（10分钟）

信息瓶颈的核心思想就是通过最大化有用的信息（即输入与标签之间的互信息），同时最小化输入与编码表示之间的互信息，来获得对任务最有用的特征表示。信息瓶颈的优化目标函数本身就是互信息的一个变种，因此，它与互信息的关系非常紧密。

MINE方法通过神经网络来估计互信息，它是利用神经网络的能力来估计两个分布之间的互信息。MINE在信息瓶颈的框架中可能有重要应用，帮助在没有显式计算互信息的情况下优化信息传递，进而增强模型的泛化能力。

内容：

《关于深度学习中信息瓶颈理论的研究》
- 研究问题：信息瓶颈理论在不同深度网络架构和任务中的适用性。
- 方法：理论分析与实验验证，观察互信息 I(X;T) 和 I(T;Y)的动态变化。
- 主要定理：
  - 定理1：在充分表示能力的深度网络中，训练初期 I(X;T) 和 I(T;Y) 增加，随后 I(X;T) 减少，I(T;Y) 稳定或略降。
  - 引理1：信息压缩阶段的出现依赖于激活函数和网络的非线性程度。
- 结论：信息瓶颈理论在具有非线性激活和深度的网络中有效，促进信息压缩和泛化能力。
  - 讨论实验设置和不同网络架构下的表现。
  - 具体说明定理和引理如何支持结论。
《利用深度变分信息瓶颈方法对黑箱模型进行解释》
- 研究问题：如何通过信息瓶颈方法解释深度模型的内部机制。
- 方法：DVIB框架，优化 $I(Z; Y) - \beta I(Z; X)$ 。
- 主要定理：
  - 定理1：DVIB通过变分下界优化，逼近信息瓶颈目标。
  - 引理1：有限样本条件下，DVIB的下界具有良好收敛性。
- 结论：DVIB在保持预测性能的同时，显著提高了模型的可解释性。
  - 解释定理和引理如何确保DVIB的有效性和稳定性。
  - 展示实验结果，说明DVIB如何识别关键特征。
《通过信息论方法揭开深度神经网络的黑箱》
- 研究问题：如何利用信息论揭示DNN内部的信息传递和表示学习过程。
- 方法：应用信息瓶颈框架，分析 I(X;T) 和 I(T;Y) 的变化。
- 主要发现：
  - 拟合阶段：I(T;Y) 增加。
  - 压缩阶段：I(X;T) 减少，I(T;Y) 稳定或略降。
  - 压缩阶段提升泛化能力。
- 结论：信息瓶颈理论成功解释了DNN的训练动态，通过信息压缩提取有用特征。

5.高维数据中的信息论应用（5分钟）

生成模型中的信息论应用 《GAN是否真正学到了分布？一些理论与实证分析》
- 研究问题：GANs是否能够从有限样本中学习并逼近真实数据分布？
- 理论框架：
  - 定理1：无限表示能力和理想优化条件下，GAN生成分布等于真实分布。
  - 定理2：有限容量的生成器和判别器下，生成分布与真实分布的差异受网络容量和样本量影响。
  - 引理1：高维空间中，GAN的样本复杂性随着数据分布复杂度指数级增长。
- 实验结果：
  - 理想条件下GAN能成功逼近真实分布。
  - 实际应用中，存在模式坍缩和未覆盖全部模态的问题。
- 结论：理论上GANs具备学习真实分布的能力，但实际受限于网络结构、训练算法和数据复杂性。
- 具体指导：
  - 网络架构改进：引入残差连接、渐进式训练等。
  - 优化算法优化：使用谱归一化、梯度惩罚等技术。
  - 正则化与多样性激励：鼓励生成器覆盖更多数据模态，避免模式坍缩。

6.总结与展望（5分钟）

信息论在机器学习和深度学习中扮演着基础而关键的角色，为模型的理论理解和实际应用提供了丰富的工具和视角。从决策树的特征选择、神经网络的损失函数设计，到信息瓶颈理论对模型训练动态的解释，再到互信息估计与表示学习优化，信息论贯穿于ML/DL模型的构建、优化与解释的各个环节。

总结：
- 信息论在特征选择、模型优化、可解释性和生成模型中的关键作用。
- 信息瓶颈理论、互信息估计、GANs的分布学习、编码率减少原则在深度学习中的具体应用。
未来方向：
- 高效信息估计：提升互信息估计方法的准确性和效率。
- 信息瓶颈与深度架构结合：深入研究信息瓶颈在不同深度架构中的应用。
- 理论与实践结合：将信息论与其他理论框架（如对比学习、强化学习）结合，提升模型性能。
- 可解释性与可控性：进一步利用信息论提升模型的透明度和生成过程的可控性。

信息论的持续发展和应用，将为机器学习和深度学习模型的理论深化和实际性能提升提供持续动力，推动智能系统向更高效、更鲁棒、更可解释的方向发展。