本文介绍了各种神经网络架构，包括前馈网络、径向基函数网络、霍普菲尔德网络、马尔可夫链、玻尔兹曼机、受限玻尔兹曼机、自编码器、稀疏自编码器、变自编码器、去噪自编码器、深度信念网络、卷积神经网络、解卷积神经网络、深度卷积逆向图网络、生成式对抗网络、循环神经网络、长短期记忆网络、门控循环单元、神经图灵机、双向循环神经网络、深度残差网络、回声状态网络和液态机。这些网络各有特点，广泛应用于机器学习和人工智能领域。
原文地址：图文并茂的神经网络架构大盘点：从基本原理到衍生关系
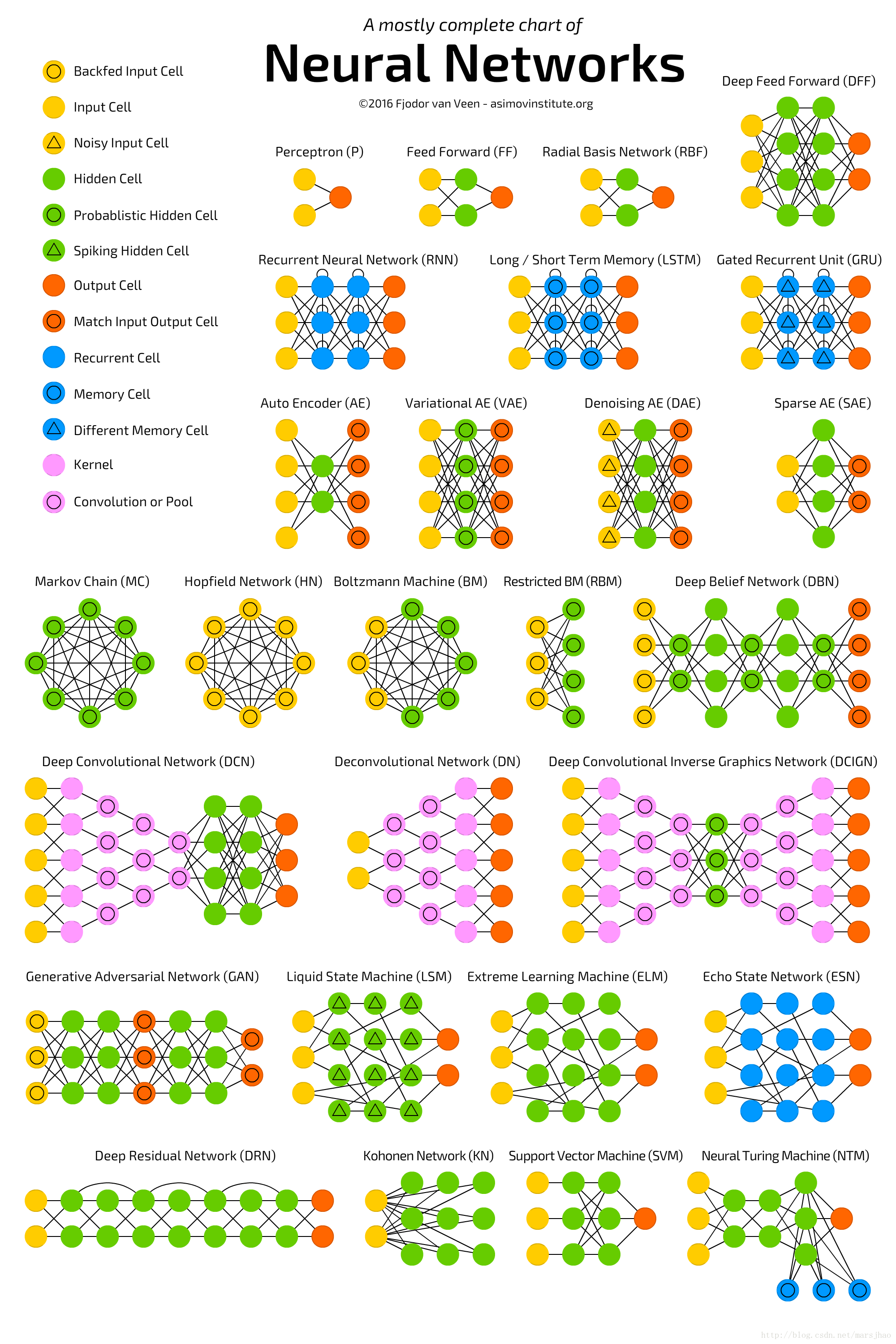
一、Neural Networks Zoo
将这些架构绘制成节点图的一个问题：它并没有真正展示这些架构的工作方式。
列出一份完整的列表实际上是不可能的，因为新架构一直在不断出现。所以尽管这份清单能为你提供人工智能世界的一些见解，但无论如何请不要认为这份清单是全面的；尤其是当你在这篇文章写出后很久才读到时（注：原文发表于 2016 年 9 月 14 日）。
二、神经网络架构简介
1. 前馈神经网络 FF
前馈神经网络（FF 或 FFNN：Feed Forwardneural networks）是非常简单的：它们从前向后馈送信息（从输入到输出）。神经网络常被描述为层级形式，其中的层（layer）可能是输入层、隐藏层或输出层。一个单独的层不存在什么连接（connection），而通常相邻的两个层是完全连接的（一个层的每一个神经元都连接到另一个层的每一个神经元）。其中可以说是最简单的实际网络具有两个输入单元和一个输出单元，其可用于对逻辑门进行建模。人们常常通过反向传播（back-propagation）来训练 FFNN，从而让该网络获得配对的数据集——「输入的内容」和「我们想要得到的输出」。这被称为监督学习（supervised learning），其相反的方法被称为无监督学习（unsupervised learning），其中我们只需要给出输入然后让网络自己填补空白。被反向传播的误差（error）常常是输入和输出之间差分（difference）的某种变体（如 MSE 或只是线性差分）。如果该网络有足够的隐藏神经元，那么理论上它总是能够建模出输入和输出之间的关系。实际上它们的使用存在很大的限制，但它们常被用来与其它网络结合以构建新的网络。
2. 径向基函数 RBF
径向基函数（RBF: Radialbasis function）网络是使用径向基函数作为激活函数（activation function）的 FFNN。这不意味着它没有用处，但大部分带有其它激活函数的 FFNN 都没有自己的专用名称。这主要是因为人们在正确的时间发明了它。
3. 霍普菲尔德网络 HN
霍普菲尔德网络（HN: HopfieldNetwork）是一种每一个神经元和其它每一个神经元都有连接的网络；其中所有的节点都是全功能的。在训练之前，每一个节点都是输入；在训练过程中，每一个节点都是隐藏；之后它们都是输出。这种网络的训练是：将神经元的值设置成我们想要的模式，从而计算出权重（weight）。之后权重便不再变化。一旦为一种或多种模式进行了训练之后，这种网络总是会收敛成其学习过的一种模式，因为这种网络只能稳定在这些状态，请注意它并不是符合预期的状态。因为该网络的总「能量（energy）」或「温度（temperature）」在训练过程中会逐渐减小，所以它总会一部分接一部分地稳定下来。每一个神经元都一个可以扩展到这个温度的激活阈值，而如果该神经元的输入总和超过了该阈值，那么输入就会使神经元从两个状态（通常是 -1 或 1，有时候是 0 或 1）之中选择一个。网络的更新可以同步完成，但更常见的是一个接一个更新神经元。如果是一个接一个地更新，就会创建一个公平随机（fair random）的序列来组织哪些单元以哪种顺序更新（公平随机是指所有（n）的选择在每 n 个项中只恰好发生一次）。这样你就能分辨网络何时达到了稳定（收敛完成）：一旦每一单元都被更新后而其中没有任何改变，那么该网络就是稳定的（即退火了的（annealed））。这些网络常被称为联想记忆（associative memory），因为其会收敛到与输入最相似的状态；人类看到半张桌子就能想象出另一半，类似地，如果给这种网络提供半张桌子和一半噪声，那么该网络就能收敛出一张桌子。
最低0.47元/天 解锁文章
扫一扫
8万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
