【辐射度量学杂记】

基本概念

辐射能量

辐射能量Radiant Energy$Q$：描述电磁场的能量，单位为焦耳J。

辐射功率

辐射功率/通量Radiant Power/Flux $P/\Phi$：单位时间的辐射能量，单位为瓦特W。
$$P=\Phi =\frac{\text{d}Q}{\text{d}t}$$

辐射照度

辐射照度Irradiance$E$：单位面积上的辐射通量，单位为W/m^2。
$$E=\frac{\text{d}\Phi }{\text{d}A}$$表面的辐射照度遵循朗伯特余弦定理Lambert’s Cosine Law。如下图所示，设光线垂直入射时照度为$E_0$，当光线与表面法线呈$\theta$角时，照度为$E\cos \theta$。

立体角

立体角Solid Angle$\Omega /\omega$：表面在球面上的投影面积与球半径平方的比值，单位为球面度sr。球的立体角为$4\pi$。

辐射强度

辐射强度Radiant Intensity$I$：单位立体角的辐射通量，单位为W/sr。通常用来描述光源朝某个方向发射的辐射功率。
$$I=\frac{\text{d}\Phi }{\text{d}\omega }$$

辐射亮度

辐射亮度Radiance$L$：单位投影面积、单位立体角的辐射通量，单位为W/sr/m^2。
$$L=\frac{{\text{d}}^2\Phi }{\text{d}\omega \text{d}{A}_{\perp }}=\frac{{\text{d}}^2\Phi }{\text{d}\omega \text{d}A\cos \theta }$$入射辐射亮度
$$L=\frac{\text{d}E}{\text{d}\omega \cos \theta }$$意为与表面法向呈$\theta$角入射的、占据立体角为$\text{d}\omega$的、辐射亮度为$L$的光线，在表面产生的辐射照度$\text{d}E=L\cos \theta \text{d}\omega$。

辐射亮度最贴近光线的概念，不会随着距离的平方衰减。辐射亮度可以通过亮度计测量。如下图所示，距物体表面一定距离，以某一角度进行观测。亮度计接收的是垂直于光学镜头光轴特定面积内的辐射通量，与辐射亮度定义中的单位投影面积对应。

相机实际是一种亮度计。相机镜头收集物体表面反射后、一定立体角中的光线。像素表面接收的辐射照度$E$与光线场景辐射亮度$L$呈正比，具体关系如下
$$E=\frac{\pi }{4}\frac{D^2}{f^2}{\cos }^4\alpha L$$其中，$D$为镜头光圈直径，$f$为镜头焦距，$\alpha$为观测点与光轴的夹角。推导过程如下图所示

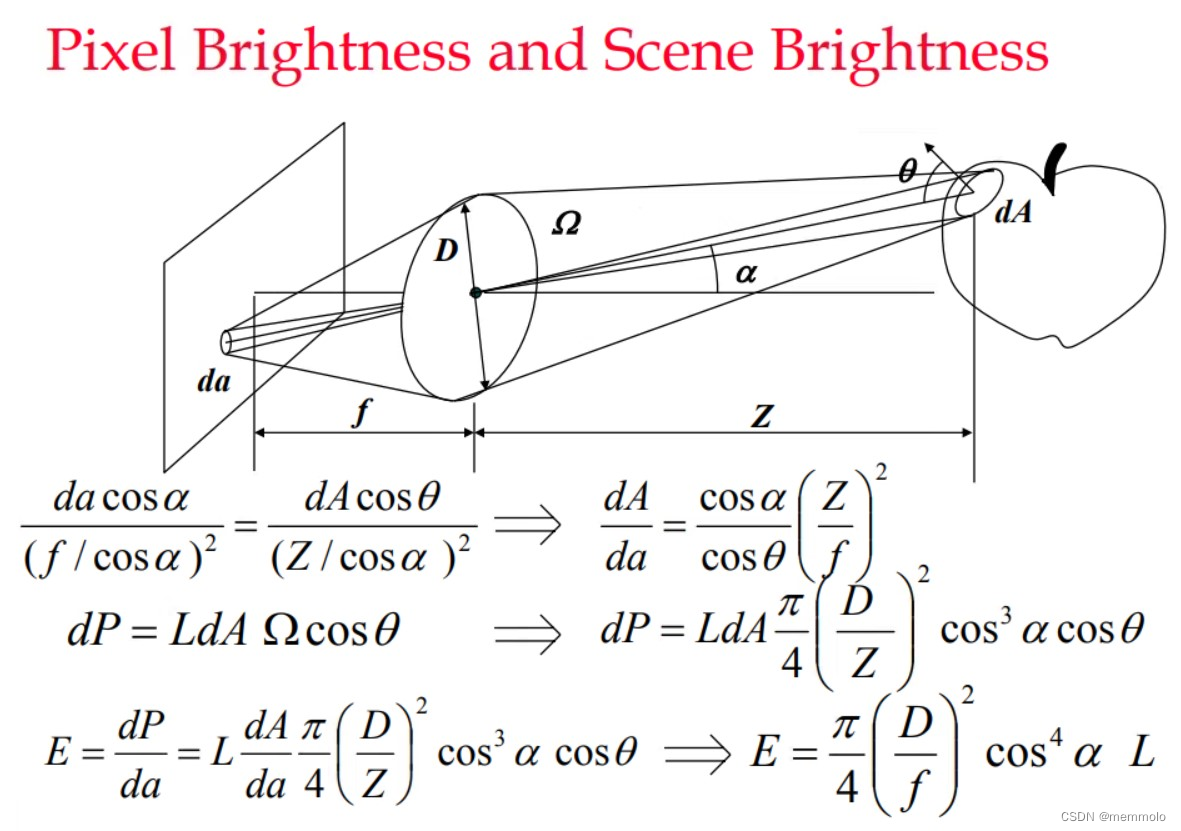
像素将接收的照度转换为灰度输出，可以参考【EMVA1288 相机噪声模型】

双向反射分布函数

双向反射分布函数Bidirectional Reflectance Distribution Function, BRDF$f_r({\omega }_i,{\omega }_o)$：描述物体表面反射特性的函数，定义为
$$f_r({\omega }_i,{\omega }_o)=\frac{\text{d}L({\omega }_o)}{\text{d}E({\omega }_i)}=\frac{\text{d}L({\omega }_o)}{L({\omega }_i)\cos \theta \text{d}\omega }$$其中${\omega }_i$为入射光线方向，${\omega }_o$为出射光线方向。

反照率为$\rho$漫反射表面的BRDF为$f_r=\frac{\rho }{\pi }$，推导过程参考Deriving Lambertian BRDF from first principles

点光源照射的漫反射平面反射的辐射亮度$L=\frac{\rho }{\pi }\frac{P}{4\pi r^2}\cos \theta$

由BRDF，可以引入渲染方程
$$L_o({\omega }_o)=L_e({\omega }_o)+\int f_r({\omega }_i,{\omega }_o)L_i({\omega }_i)\cos \theta \text{d}{\omega }_i$$其中，$\text{d}E({\omega }_i)=L_i({\omega }_i)\cos \theta \text{d}{\omega }_i$为入射光在物体表面产生的辐射照度，$L_e$为物体自发光辐射亮度。

辐射度量学与光度学单位

辐射度量学	Radiometry	单位	符号	光度学	Photometry	单位
辐射能量	Radiant Energy	$J$	$Q$	光能量	Luminous Energy	Talbot(T) = $lm\cdot s$
辐射功率/通量	Radiant Power/Flux	$W$	$P,\Phi$	光通量	Luminous Flux	Lumen(lm) = $cd\cdot sr$
辐射照度	Irradiance	$W/m^2$	$E$	光照度	Illumiance	Lux(lx) = $cd\cdot sr/m^2$ = $lm/m^2$
辐射强度	Radiant Intensity	$W/sr$	$I$	光强度	Luminous Intensity	Candela(cd)
辐射亮度	Radiance	$W/(m^2\cdot sr)$	$L$	光亮度	Luminance	nit = $cd/m^2$