光学系统是一个传输辐射能量的系统,能量传输能力得强弱,影响像的亮暗。辐射度学是研究电磁波辐射的测量计量计算的学科。光度学是在人眼视觉的基础上,研究可见光的测试计量计算的学科。
一、立体角
1、立体角的意义和单位
平面上的角,若以
为半径的圆周上截得弧长为
,则此平面角为1平面弧度;若截得弧长为
,对应平面角为
弧度,也可表示为360°。

立体角---一个任意形状的封闭锥面将所包含的空间,。如下图,半径为
的球面上,表面积
对应的立体角为1球面度,整个空间球面面积
对应立体角为
。

2、立体角的计算
假设一个光学系统,其物方孔径角为,由轴上物点发出孔径角为
的圆锥空间所包含的立体角为
。当
较小时,

推导过程: 假定圆锥面的半顶角为,以锥顶为原点,
为半径做一个圆球,假定在圆球垂直于
轴方向上取一个锥角
增量为环带,则环带宽度为
,环带半径为
,环带周长为
,
球表面上环带的面积为,
对应立体角增量为
两端积分得

二、辐射度学中的基本量及其计量单位
1、辐射通量
- 辐射通量是单位时间内辐射体辐射的总能量,称辐射功率,单位是瓦特(W)。
- 它反映了辐射强弱,是辐射体各波段辐射能量的积分。
- 计算
,

2、辐射强度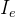
- 辐射强度表示的是辐射体在某一特定方向上单位立体角范围内的辐射通量。
- 反映了辐射体在不同方向上的辐射特性
- 计算
,单位:瓦每球面度(
)

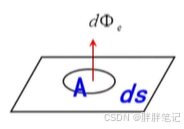
3、辐射出射度 
- 辐射出射度是指辐射体上某一点附近某一微元面积上辐射的总辐射度通量。
- 它不管向哪个方向辐射,描述的是辐射体表面不同位置上单位面积的辐射特性。
- 计算:
,单位:瓦每球面度(
)
4、辐射照度
- 辐射照度与辐射出射度正好相反,不是发出辐射通量,而是某一微元面积上接收的总辐射通量。
- 计算
,单位:瓦每球面度(
)

5、辐射亮度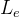
- 辐射亮度指的是在某一指定方向上单位立体角内单位投影面积上发出的辐射通量
- 描述了辐射体在不同位置不同方向上的辐射特性。
- 计算:
,单位:瓦每球面度每平方米(
)

三、人眼的视见函数 
光度学中,为了表示人眼对不同波长辐射的敏感度差别,定义了一个函数 ,称为视见函数,又称为光谱光视效率。
,人眼对
的光最灵敏。

四、光度学中的基本量
利用人眼视见函数,可以将辐射度学中的基本量转变为光度学中的基本量。一般来说,加如角标e的为辐射度学基本量,不加角标e为光度学基本量。
1、光通量 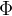
光度学中的光通量与辐射度学中的辐射通量相对应。假定有一单色光,其辐射度,其中能够引起视觉的部分为光通量---用人眼视觉强度来度量的辐射通量。
单位:流明,。C为单位换算常数,
光谱光视效能
-
与
的乘积称为光谱光视效能,用
表示。
表示辐射通量中有多少可以转变为光通量。
- 当
时,
,称为最大光谱光视效能。
连续光谱的光通量的计算
有了光谱光视效能后,光通量公式可写为
总的光通量等于整个波长范围内上式的积分
发光体的发光特性---光视效能
2、发光强度 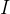
发光强度与辐射度学中的辐射强度相对应,指的是指定方向上单位立体角内发出光通量的多少,单位:坎德拉(cd)
3、光出射度 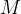
光出射度发与辐射度学中的辐射出射度相对应,指的是发光体表面某点附近单位面积发出的光通量。单位:
发光表面均匀发光情况下,、
4、光照度 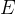
光照度与辐射度学中的辐射照度相对应,指的是某一表面某点附近单位面积接收的光通量。单位:勒克斯(),
被照表面均匀的情况下,。
5、光亮度 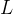
光亮度与辐射度学中的辐射亮度相对应,指的是发光体表面某点附近微元面积在某一方向上单位立体角内发出的光通量,描述了发光体某点在给定方向上的发光特性。单位:
五、光照度公式和发光强度余弦定律
1、光照度公式
假定点光源照明微小平面,
离光源距离为
,表面法线方向与照明方向夹角为
,若光源再次方向上发光强度为
,求光源在
上的光照度。

上式即为光照度公式 ,此公式是在点光源情况下导出的,对于发光面积和照明距离相对很小的情况下也可以用。发光面积大时,就不能使用了,但远距离照明可以使用。
- 光照度公式可运用于测定光源发光强度

两个完全相同的漫反射表面,标准光源已知,用眼睛观察两表面,由光照度公式
移动待测光源,改变,即改变
,当眼睛观察两表面同时亮时(E相等),测出
,由
得出
2、发光强度余弦定律
在各方向上光亮度都相等的均匀发光体称为朗伯辐射体

假定发光微面在与该微面垂直方向上的发光强度为
,发光体各方向光亮度一致
由此可得到发光强度余弦定律,也称朗伯定律,符合余弦定律的发光体称为余弦辐射体或郎伯辐射体
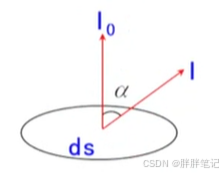
- 朗伯定律可用于求发光微面发出的光通量。
已知发光微面,光亮度
,求它在半顶角为
的圆锥内所辐射的总光通量

微小立体角内,半顶角为u的圆锥对应的立体角为
,光通量
,其中
,
,
,代入得:
单面发光:,
;
双面发光:
六、全扩散表面的光亮度
如果被照明物体表面由于漫反射作用使它在各个方向上光亮度相同,则称这样的表面为全扩散表面。例如白纸、喷粉的墙壁、白灰、电影银幕等
全扩散表面面积,光照度
,全扩散表面光亮度
。推导如下:
表面接受的光通量
全扩散表面发出的光通量,
为漫反射系数,表示百分之多少的光通量漫反射出去。
全扩散表面可以看成是单面发光的光源
由此得出,全扩散表面光亮度。
七、光学系统中光束的光亮度
1、在均匀介质中传播

选取垂直于光束的横截面,光亮度
由输入到
上的光通量
由发出的光通量
不考虑光能损失,输入到上的光通量
应该等于
发出的的光通量
,即
,化简后得到
。
在均匀透明的介质中,如果不考虑光能损失,位于同一条光线上的各点,在光线进行的方向上光亮度不变。
2、折射情况
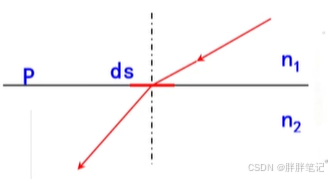

在法线分界面处以半径作圆,在入射平面,给入射角
一个增量
,入射光线由
移动到
。再将圆沿着法线旋转
角,矩形
面积与
的比值即为立体角增量
,即
入射光光亮度
同理,折射光光亮度
假设没有光能量损失,即,则可得到
利用折射定律,![]() ,则
,则。
综上,折射时入射光线和反射光线的光亮度满足
3、反射情况
反射可以看作的情况,反射时入射光线和反射光线的光亮度满足
综上,光束的光亮度
存在普偏关系式
,
称为折合光亮度。
如果不考虑光束在传播过程中的光能损失,则位于同一条光线上的所有各点,在该光束传播方向上的折合光亮度不变。
4、理想光学系统中像的光亮度

实际光学系统中,考虑光能损失,
其中,
为光学系统的透过率。
八、像平面的光照度
1、轴上点的光照度
已知成像物体光亮度,像方孔径角
,像面光照度为
。推导如下

由单面发光发光强度公式推导过程可知,像方光通量为
由此,像面光照度为
引入理想光学系统中像的光亮度公式,则
如果物像处于同一介质中,
2、轴外点光照度
像平面轴外点的光照度小于轴上点的光照度。这是由于轴外光束倾斜后,出瞳再光束垂直方向上的投影面积减小,轴外点的发光强度比轴上点的发光强度小,
。照明距离比轴上点的照明距离增加
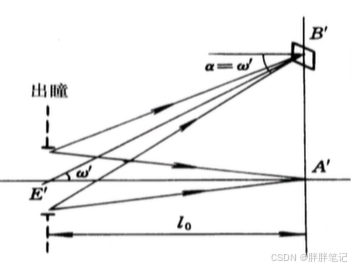
像方光照度,
因为可能存在渐晕,还需乘以渐晕系数,
九、照相物镜像平面的光照度和光圈数
1、像平面光照度

对于照相机物镜,代入,
定义相对孔径
2、光圈
相对孔径,分度的办法是按照每一刻度对应的像面照度减少一半,相对孔径按照的等比级数变化。
光圈数---相对孔径的倒数,用F表示,称F制光圈。
此外,因为光照度公式中带有透过率,定义T制光圈,
3、曝光量
假定像面照度为 E,曝光时间为 t,底片上单位面积接受的曝光量为
十、人眼的主观光亮度
1、基本概念
1)主观光亮度
- 定义:外界物体对人眼的刺激强度
- 特点:人眼对亮暗的感觉,属于主观范畴
- 表示方法:主观光亮度可以用具体的光度学的量来表示。不同外界物体对应不同物理量。
2)外界物体分类
- 发光点:发光体对人眼的视角很小,在视网膜上所成的像小于一个视神经细胞的直径
- 发光面:发光体对人眼张角较大,在视网膜上所成的像有一定面积
2、人眼直接观察发光点的主观光亮度

- 衡量标准:进入人眼的光通量表示主观光亮度
- 计算公式
3、人眼对发光面的主观光亮度

- 衡量标准:人眼像平面的光照度表示主观光亮度
- 计算公式:
十一、通过望远镜观察的主观光亮度
1、发光点
1)望远镜出瞳小于等于眼睛瞳孔直径

进入仪器的光通量
从仪器出来的光通量,
----仪器的透过率
通过仪器观察的主观光亮度
与人眼直接观察相比
2)望远镜出瞳大于眼睛瞳孔直径
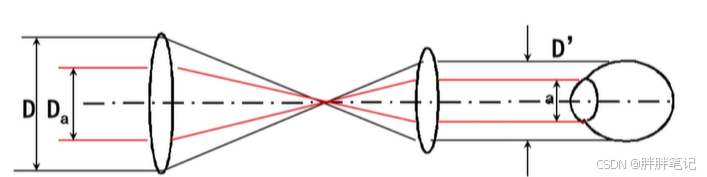
通过仪器观察的主观光亮度
与人眼直接观察相比
2、发光面
1)望远镜出瞳小于眼睛瞳孔直径
2)望远镜出瞳大于等于眼睛瞳孔直径
无论望远镜出瞳直径大于、等于还是小于人眼瞳孔直径,在通过望远镜观察发光面时,主观光亮度都小于直接观察发光面时的主观光亮度。
十二、光学系统中光能损失的计算
1、光能损失的原因
- 光束在光学零件表面的反射
- 光束通过介质时的吸收
2、光能损失的影响
- 光学系统成像光亮度降低
- 像的清晰度下降
- 形成寄生像
3、反射损失计算
反射系数:介质分界面反射光通量和入射光通量之比。
假定入射光通量,折射光通量
,反射光通量为
,能量守恒
代入反射系数可知

若不考虑介质吸收损失,从第一个表面折射的光通量即第二个表面的入射光通量
对于具有K个折射面的系统
4、吸收损失计算
- 入射光通量越大,吸收越大,光线走的路程越长,吸收越大。
- 计算公式
。
为介质宽度;
为介质的透明系数。
时,
,光束通过单位长度介质时,出射和入射光通量之比。

假定进入的光通量为
,通过
后变化了
,
对上式积分可得
令,
综合考虑光能的反射和吸收,当系统中有m个折射表面和n中介质时,
光学系统透过率
常用透射率公式
表面镀增透膜后的透过率
-
:镀铝面数
-
:镀银面数
-
:冕牌玻璃和空气接触面数
-
:火石玻璃和空气接触面数
-
:沿光轴计算的玻璃总厚度(以厘米为单位)
十三、投影仪的作用及其类别

1、投影仪
- 作用:把一定大小的物体用光源照明后成像到屏幕上进行观察和测量;
- 种类:电影放映机、幻灯机、投影仪等;
- 要求:成像清晰,物像相似;像面有足够的光照度,分布均匀
2、投影系统的组成
- 投影物镜:把一定大小的物体成像在屏幕上,使成像清晰,物像相似
- 照明系统:照明物体,充分利用光源发出的光能,并使照明均匀。
3、投影系统分类
1)临界照明
光源通过照明系统成像在物平面上,照亮物体;物体再经投影物镜成像在屏幕上。

- 反射照明

- 透射照明

2)柯勒照明
光源通过照明系统成像在投影物镜的入瞳上,物体再经过投影物镜成像在屏幕上。

十四、投影系统中的光能计算
1、已知投影系统结构参数,求像平面光照度
假定一个35mm的电影放映机,采用电弧作光源,要求屏幕照度为100,放映机离开银幕距离为50m,银幕宽7m,求放映物镜的焦距和相对孔径。
35mm电影机的片框尺寸为,要求放映物镜的放大率为
根据牛顿放大率公式可知
其中,由于像距比焦距大很多,,计算得出
根据本文第八部分,像平面光照度公式可知,
由几何关系可知,物镜的口径
放映物镜的相对口径
照明系统得光学系统计算

假定片门离照明反射镜的距离为850mm,由三角形相似可知,所以反射镜的口径为
假定电弧焰口的直径为9mm,片门的对角线尺寸为27mm,反射镜将电弧放大。根据放大率公式
可知,焰口像的直径
能够覆盖片门,由放大率,像距
,对于反射情形
根据放大率公式可知
因为在物像均在空气中,并且为反射,所以,代入高斯公式,得
2、已知像平面光照度,求投影系统和照明系统结构参数
一个小型投影仪采用6V30W得白炽灯照明。灯泡的光视效能为,灯丝为直径3mm,长3mm的螺线管。投影物镜的焦距为50mm,相对孔径1:3.5,放大率为
,投影仪光学系统如下图所示。采用柯勒照明方式,照明系统的放大率
,系统透过率
,求像平面光照度

根据本文第四部分,光源发出的总光通量
假定各方向均匀发光,根据本文部分,发光强度
光亮度
考虑后面加了球面反光镜,平均光亮度提高50%,则得到发光体的平均光亮度
照明系统放大率,因此,投影物镜的有效通光面积为

通光区域为圆形,需要将正方形等效为相当的圆形,相当的通光孔径
根据牛顿放大率公式,投影物镜的放大率为
,焦距为50mm,像距
为
像方孔径角
根据本文第八部分,像平面光照度公式可知,























 1320
1320

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








