克拉克变换和帕克变换的数学原理和算法实现

最新推荐文章于 2025-03-22 17:51:56 发布

mftang

最新推荐文章于 2025-03-22 17:51:56 发布

阅读量2.7k

点赞数 30

分类专栏： FOC算法文章标签：算法

本文链接：https://blog.csdn.net/mftang/article/details/145711654

版权

FOC算法专栏收录该内容

12 篇文章

订阅专栏

2 Clarke Transform 实现原理

2.2 Inverse Clarke Transform

2.2.1 转换方法

2.2.2 转换波形

2.2.3 数学原理

3 Park Transform 实现原理

3.2 Inverse Park Transform

概述

本文主要介绍克拉克变换和帕克变换的原理和算法实现，同时介绍了克拉克变换的逆变换和帕克变换的逆变换，并给出推导数学计算和验证波形图。

1 克拉克和帕克变换的定义

1.1 克拉克变换

克拉克变换和帕克变换等坐标变换在三相交流电机的FOC中的应用很常见。克拉克变换将三相系统（在 abc 坐标系中）的时域分量转换为正交静止坐标系 (αβ) 中的两个分量。

图一：三相系统（在 abc 坐标系中）的时域分量

上图的波形经过Clark变换之后，会将其转换为两相的αβ坐标系

图二：克拉克变换 (αβ) 生成的信号

1.2 帕克变换

帕克变换将 αβ 坐标系中的两个分量转换为正交旋转参考坐标系 (dq) 中的分量。以连续方式实现这两种变换可简化计算，因为它们能够将交流电流和电压波形转换为直流信号。

图二：帕克变换生成(dq) 的信号

2 Clarke Transform 实现原理

2.1 Clarke Transform

2.1.1 转换方法

Clarke Transform 模块计算 abc 参考系中平衡三相分量的克拉克变换，并输出静止 αβ 参考系中平衡两相正交分量。该模块也可以计算三相分量 a、b 和 c 的克拉克变换，并输出分量 α、β 和 0。对于平衡系统，零分量等于零。使用输入数参数以使用两个或三个输入。

使用双输入配置时，该模块接受三相 (abc) 中的两个信号，自动计算第三个信号，并输出 αβ 参考系中的对应分量。

例如，该模块接受 a 和 b 输入值或多路复用输入值 abc，其中相位 a 轴与 α 轴对齐。

图一：定子绕组在 abc 参考系和静止 αβ 参考系中的磁轴方向

图二：静止 αβ 参考系中的等效 α 和 β 分量

2.1.2 转换波形

等效平衡的 abc 和 αβ 系统的单个分量的时间响应

经过 Clarke Transform之后，形成 αβ 系统的波形，具体图像如下：

2.1.3 数学原理

以下方程描述克拉克变换计算：

对于电机等平衡系统，零序分量计算始终为零。例如，电机的电流可以表示为：

因此，在三相电机驱动中可以只使用两个电流传感器，可以将其中的第三相计算为：

通过使用以下方程，该模块将克拉克变换实现为：

参数介绍：

fa、fb 和 fc 是 abc 参考系中的平衡三相分量。

fα 和 fβ 是静止 αβ 参考系中的平衡两相正交分量。

f0 是静止 αβ 参考系中的零分量。

2.2 Inverse Clarke Transform

2.2.1 转换方法

Inverse Clarke Transform 模块计算静止 αβ 参考系中平衡的两相正交分量的克拉克逆变换，并输出静止 abc 参考系中平衡的三相分量。该模块也可以计算分量 α、β 和 0 的克拉克逆变换，以输出三相分量 a、b 和 c。对于平衡系统，零分量等于零。使用输入数参数以使用两个或三个输入。

该模块接受 α-β 轴分量作为输入，并输出对应的三相信号，其中相位 a 轴与 α 轴对齐。

图一： αβ 参考系中的 α 和 β 输入分量

图二： abc 参考系和 αβ 参考系中等效的 a、b 和 c 输出分量的方向

2.2.2 转换波形

等效平衡的 αβ 和 abc 系统的单个分量的时间响应。

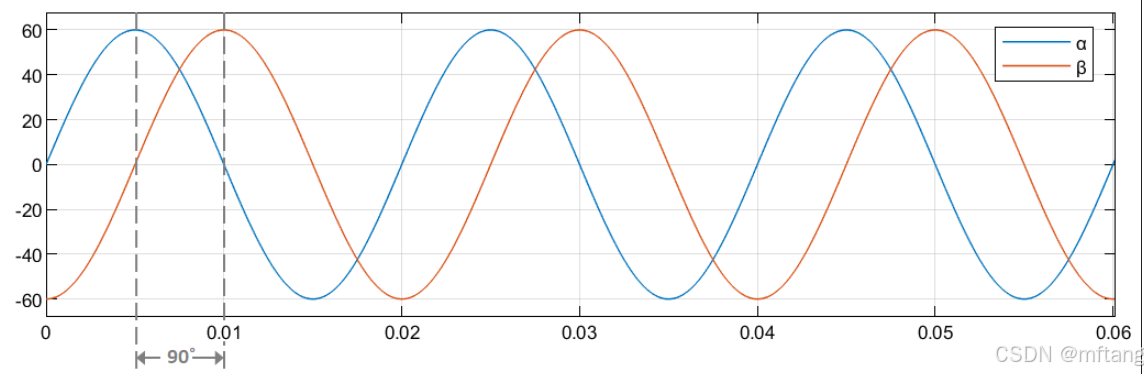
经过 Inverse Clarke Transform 后，得到 abc 系统的波形图

2.2.3 数学原理

以下方程描述了克拉克逆变换计算：

对于电机等平衡系统，零序分量计算始终为零：

ia+ib+ic=0

因此，在三相电机驱动中可以只使用两个电流传感器，您可以将其中的第三相计算为，

ic=−(ia+ib)

通过使用以下方程，该模块将克拉克逆变换实现为：

参数介绍：

fα 和 fβ 是静止 αβ 参考系中的平衡两相正交分量。

f0 是静止 αβ 参考系中的零分量。

fa、fb 和 fc 是 abc 参考系中的平衡三相分量。

3 Park Transform 实现原理

3.1 Park Transform

3.1.1 转换方法

Park Transform 模块计算静止 αβ 参考系中两相正交分量（α、β）或多路复用 αβ0 分量的帕克变换。该模块接受以下输入：

静止参考系中的 α-β 轴分量或多路复用分量 αβ0。使用输入数参数以使用两个或三个输入。

对应变换角度的正弦值和余弦值。

在使用双输入配置时，它会输出旋转 dq 参考系中的正交直轴 (d) 和交轴 (q) 分量。在使用三输入配置时，它输出多路复用分量 dq0。

对于平衡系统，零分量等于零。

可以配置模块，使 d 轴或 q 轴在时间 t = 0 处与 α 轴对齐。

下列各图显示在以下情形下 αβ 参考系和旋转 dq 参考系中的 α-β 轴分量：

图一：d 轴与 α 轴对齐

图二： q 轴与 α 轴对齐

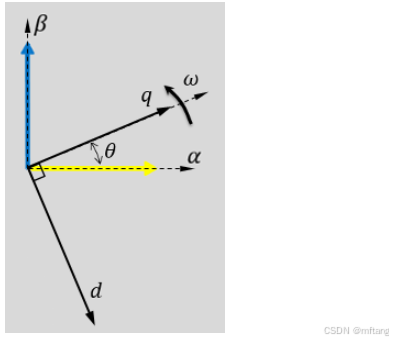
在这两种情形下，角度 θ = ωt，其中：

θ 是 d 轴对齐时 α 轴和 d 轴之间的夹角，或是 q 轴对齐时 α 轴和 q 轴之间的夹角。它指示旋转 dq 参考系相对于 α 轴的角位置。

ω 是 d-q 参考系的转速。

t 是从初始对齐开始的时间，以秒为单位。

3.1.2 转换波形

下列各图显示 αβ 和 dq 参考系的各个分量在以下情形的时间响应：

图一：d 轴与 α 轴对齐。

图二：q 轴与 α 轴对齐。

3.1.3 数学原理

以下方程描述模块如何实现帕克变换。

当 d 轴与 α 轴对齐时：

当 q 轴与 α 轴对齐时：

其中：

fα 和 fβ 是静止 αβ 参考系中的两相正交分量。

fd 和 fq 是旋转 dq 参考系中的直轴和交轴正交分量。

3.2 Inverse Park Transform

3.2.1 转换方法

Inverse Park Transform 模块计算正交直轴 (d) 和正交轴 (q) 分量或旋转 dq 参考系中的多路复用 dq0 分量的帕克逆变换。可以对该模块进行配置，使 d 轴或 q 轴在时间 t = 0 处与 α 轴对齐。

该模块接受以下输入：

旋转参考系中的 d-q 轴分量或多路复用分量 dq0。使用输入数参数以使用两个或三个输入。

对应变换角度的正弦值和余弦值。

在使用双输入配置时，它输出静止 αβ 参考系中的两相正交分量。在使用三输入配置时，它输出多路复用分量 αβ0。对于平衡系统，零分量等于零。

下列各图显示在以下情形下的旋转 dq 参考系和 αβ 参考系中的 α-β 轴分量：

图一：d 轴与 α 轴对齐

图二：q 轴与 α 轴对齐

在这两种情形下，角度 θ = ωt，其中：

θ 是 d 轴对齐时 α 轴和 d 轴之间的夹角，或是 q 轴对齐时 α 轴和 q 轴之间的夹角。它指示旋转 dq 参考系相对于 α 轴的角位置。

ω 是 d-q 参考系的转速。

t 是从初始对齐开始的时间，以秒为单位。

3.2.2 转换波形

下列各图显示 αβ 和 dq 参考系的各个分量在以下情形的时间响应：

图一：d 轴与 α 轴对齐

图二：q 轴与 α 轴对齐

3.2.3 数学原理

以下方程描述了该模块如何实现帕克逆变换。

当 d 轴与 α 轴对齐时：

当 q 轴与 α 轴对齐时：

其中：

fd 和 fq 是旋转 dq 参考系中的直轴和交轴正交分量。

fα 和 fβ 是静止 αβ 参考系中的两相正交分量。

参看文献：

https://ww2.mathworks.cn/help/mcb/ref/inverseparktransform.html