一、曲面方程和空间曲线方程的概念
1.引入原因
平面与空间直线是曲面和空间曲线的特例,为了讨论二者引入。
2.几何意义
在空间解析几何中,任何曲面或曲线都是点的几何轨迹。
可以通过判断点是否满足曲线或曲面的方程来判断它在不在曲面上。
二、平面的点法式
1.法线向量
(1)一个非零垂直于一平面的向量。
(2)平面上任意向量都垂直于法线向量。
(3)过空间一点可以作且只能作一平面垂直于一直线(我的理解是 知道平面上一点的坐标和法向量,可以确定一个平面)。
(4)求法线向量可以由两个向量叉乘求得。
2.点法式
同济课本上给的例题:
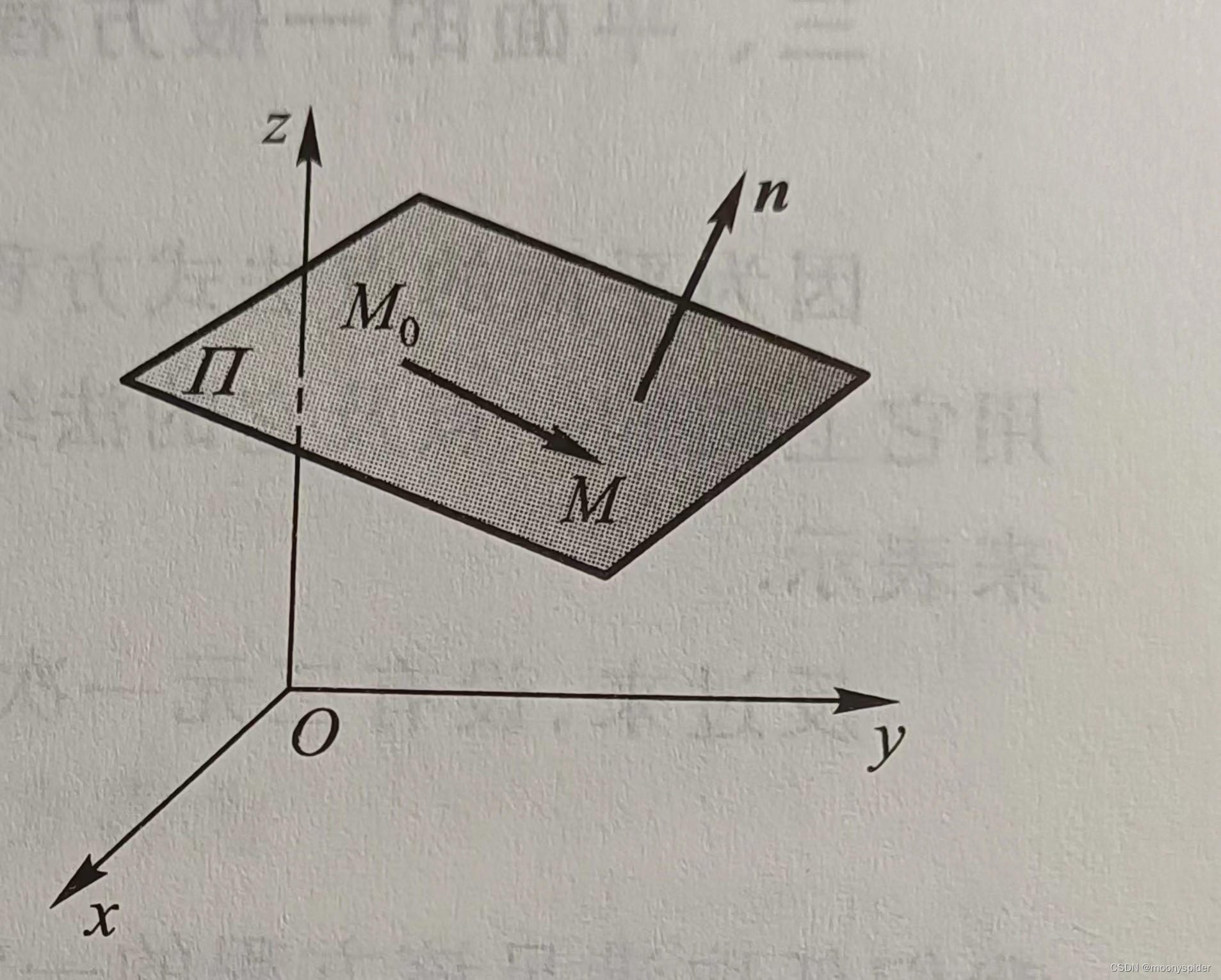
如图,已知的条件是:
(1)M0的坐标(x0,y0,z0);
(2)法线向量n(A,B,C);
为了求平面方程,要先确认一点:平面上所有向量与法线向量都垂直。这也就意味着平面上所有的向量与法线向量的点乘都为0(因为垂直了),本质上其实就是一个点乘的问题。
设任意点为M(x,y,z),向量MoM和n的点乘结果为0,即:
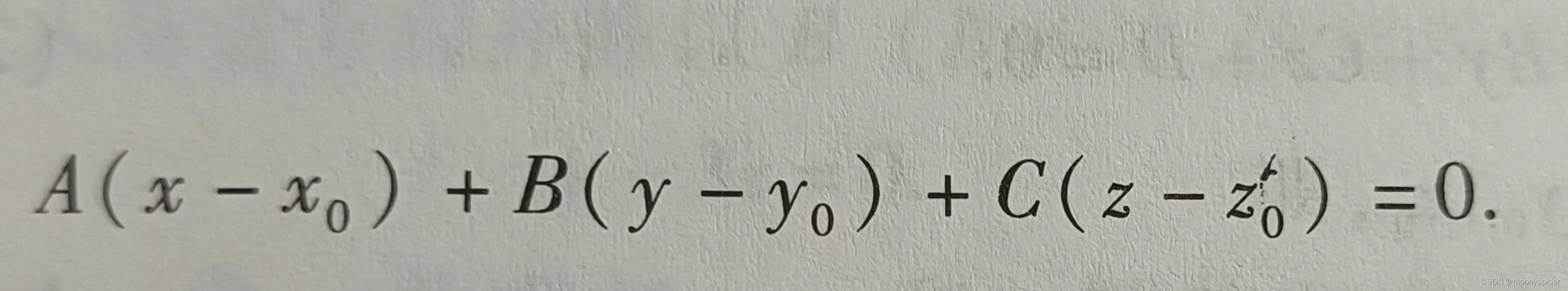
这个式子就叫做点法式。
三、平面的一般方程
1.和点法式的联系
任意平面都可以用平面上一点来表示,所以由点法式方程可以看出,任何平面都可以用三元一次方程表示。
2.推导过程
(1)设一个三元一次方程:Ax+By+Cz+D=0
(2)取任意一组数x0,y0,z0:Ax0+By0+Cz0+D=0
(1)(2)相减可得 :
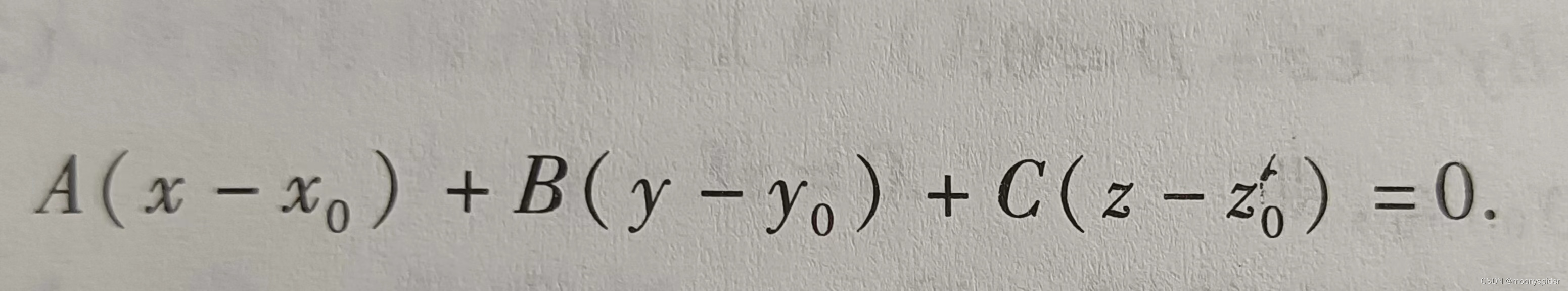
3.一般方程
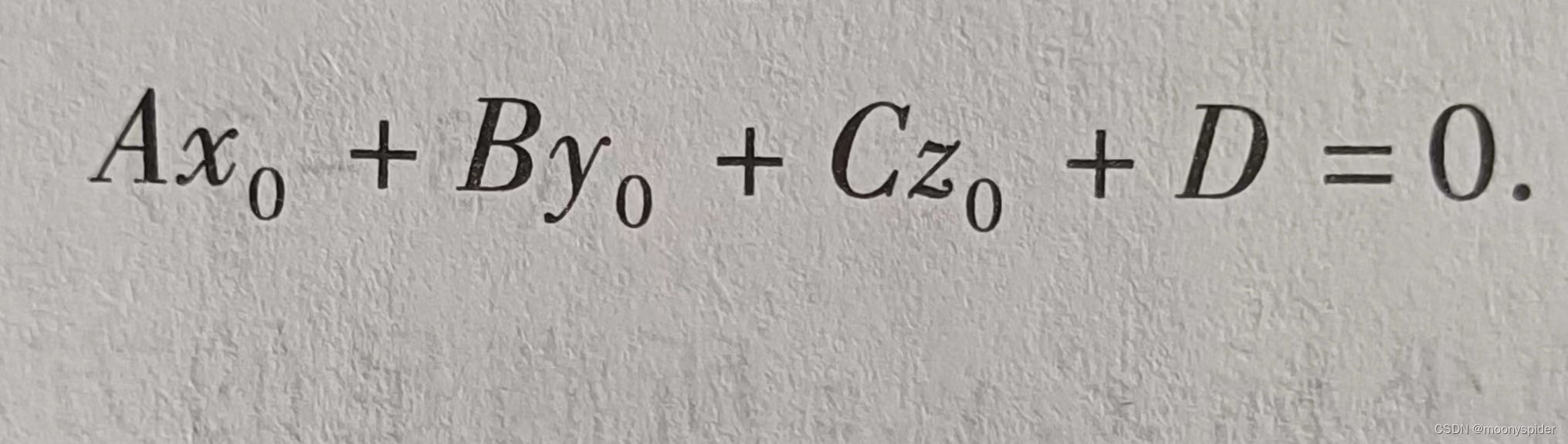
四、两平面的夹角
1.法向量的夹角
在点乘之中,我们知道a .b=|a| |b| cos,即

夹角的余弦值等于两个向量相乘再除以它们的模的乘积。
cos=
两个法向量的夹角求法也是一样的,只不过需要注意法向量的夹角是平面之间夹角的锐角,即:
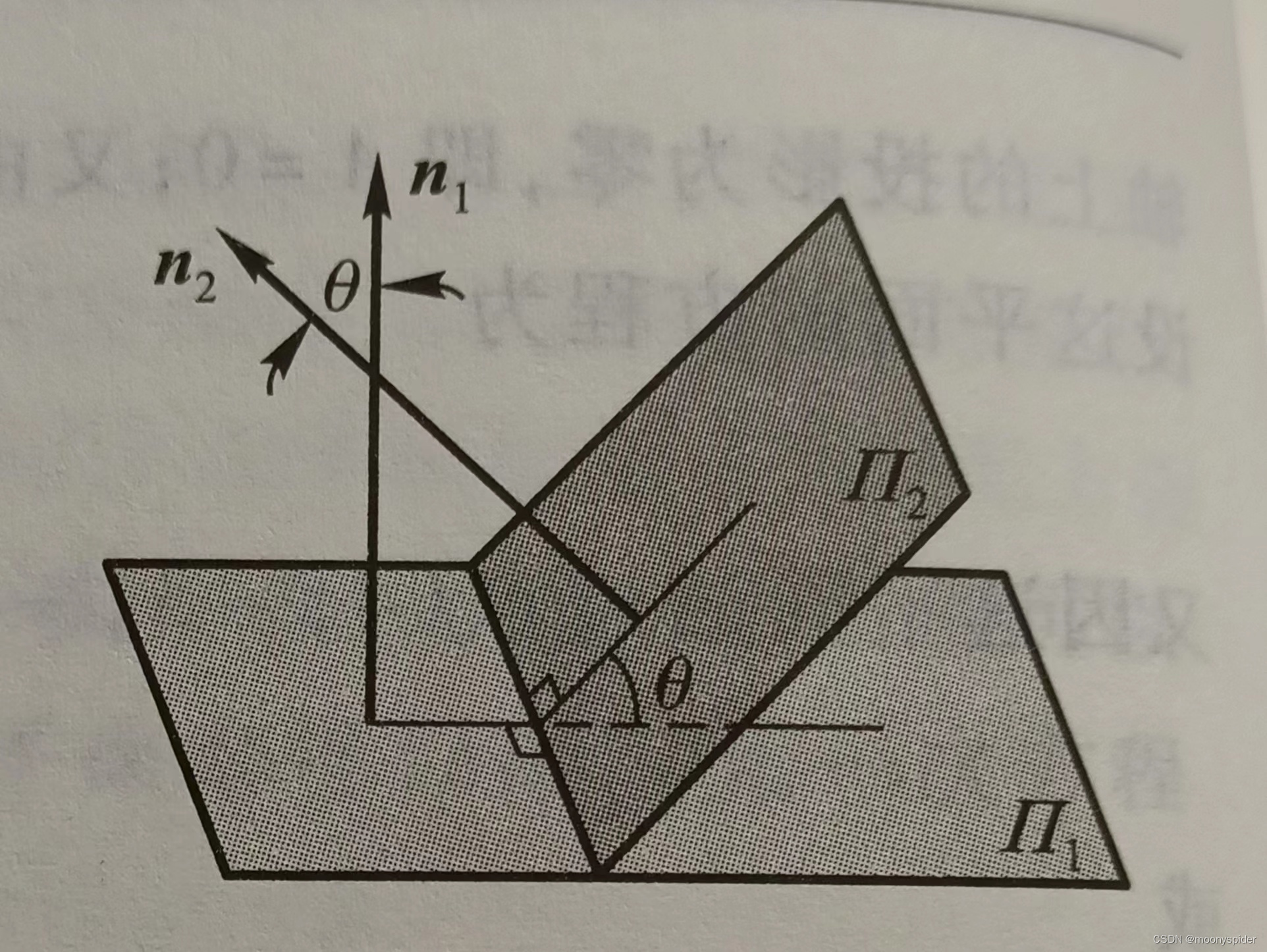




 本文探讨了曲面方程和空间曲线的基本概念,重点介绍了平面的点法式,包括法线向量的定义与求法,以及如何通过点法式表示平面并求其一般方程。此外,还涵盖了两平面夹角的计算方法。深入浅出地讲解了这些在信息技术中的应用。
本文探讨了曲面方程和空间曲线的基本概念,重点介绍了平面的点法式,包括法线向量的定义与求法,以及如何通过点法式表示平面并求其一般方程。此外,还涵盖了两平面夹角的计算方法。深入浅出地讲解了这些在信息技术中的应用。
















 2717
2717

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








