之前我们了解了神经网络模型(Nerual Network),这一次,我们来具体讨论一下神经网络模型的表达。
我们知道,神经网络模型是许多逻辑单元(Logistics Unit)按照不同的层级组织起来的网络,每一层的输出变量作为下一层的输入变量。如下图,是一个三层的神经网络,第一层为输入层(Input Layer),最后一层为输出层(Output Layer),中间的一层为隐藏层(Hidden Layer)。我们为每一层都增加一个偏倚单位(Bias Unit):
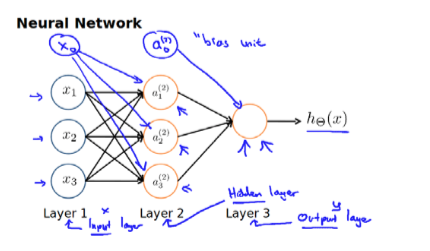
下面呢,我们引入一些标记法来帮助我们描述模型:
对于上面的图示的模型,激活单元和输出分别表达为:
到目前,我们讨论的只是将特征矩阵中的一行(也就是一个训练实例)喂给了神经网络,事实上我们需要将整个训练集都喂给我们的神经网络算法来学习模型。
正向传播(Forward Propagation)
相对于使用循环来进行编码,利用向量化的方法会使得计算更为简单快捷。
我们就使用上面的神经网络为例,试着计算第二层的值:
我们令:
则:
计算之后添加:
则计算输出的值为:
我们令:
则:
这只是针对训练集中一个训练实例所进行的计算。如果我们要对整个训练集进行计算,我们需要将训练集特征矩阵进行转置,使得同一个实例的特征都在同一列里,即:
对神经网络的一些理解
从本质上讲,神经网络能够通过学习得出其自身的一系列特征。在之前我们讨论过的普通的逻辑回归(Logistic Regression)中,我们被限制为使用数据中的原始特征x1,x2,...,xn,我们虽然可以使用一些二项式项来组合这些特征,但是我们仍然受到这些原始特征的限制。在神经网络中,原始特征只是输入层,像我们上面的那个三层神经网络的例子中,第三层,也就是输出层,做出的预测利用的是第二层的特征,而非输入层中的原始特征,我们可以认为第二层中的特征是神经网络通过学习之后,自己得出的一系列用于预测输出变量的新特征。
神经网络的一些示例:二元逻辑运算符(Binary Logical Operators)
当输入的特征为布尔值(0或1)时,我们可以使用一个单一的激活层可以作为二元逻辑运算符,为了表示不同的运算符,我们只需要选择不同的权重即可。
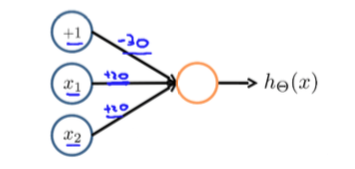
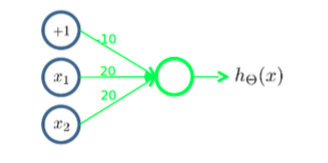
如下图,神经元(三个权重分别为-30,20,20)可以被视为作用同逻辑与(AND):
下面的神经元(三个权重分别为-10,20,20)可以被视为作用同逻辑或(OR):
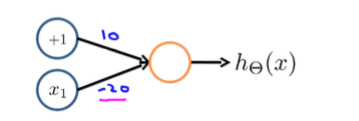
下图的神经元(两个权重分别为10,-20)可以被视为作用同逻辑非(NOT):
我们可以利用神经元来组合成更为复杂的神经网络以实现更加复杂的运算。例如,我们要实现XNOR功能(输入的值必须一样,都为1或都为0),即 XNOR = (X1 AND X2) OR ((NOT X1)AND(NOT X2))。
首先,构造一个能够表达(NOT X1)AND(NOT X2)部分的神经元:
然后将表示AND的神经元和表示(NOT X1)AND(NOT X2)的神经元,以及表示OR的神经元进行组合:
这样,我们就得到了一个能够实现XNOR运算符功能的神经网络了。
多类分类
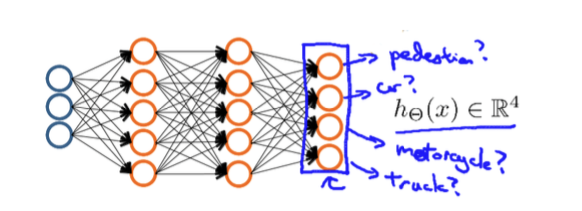
假设,我们要训练一个神经网络算法来识别路人、汽车、摩托车和卡车,在输出层,我们应该有4个不同的值。例如,第一个值为1或0用来预测是否是行人,第二个值用来判断是否是汽车等等。
下图表示,该假设的神经网络的一种可能结构:
神经网络算法的输出结果,为四种情况可能情形之一:
综上,我们深入探讨了一下神经网络模型的表达、二元逻辑运算符等神经网络的内容,下一次我们讨论神经网络学习的问题。










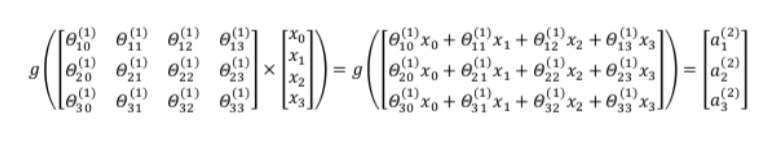

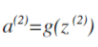
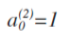
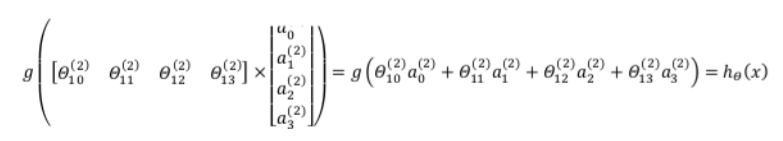
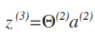

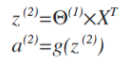


















 6万+
6万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










