主流向量数据库使用

原创已于 2025-05-15 12:27:40 修改

· 1k 阅读

21 ·

版权

文章标签：

#人工智能 #语言模型

于 2025-05-12 13:23:27 首次发布

大模型专栏收录该内容

34 篇文章

订阅专栏

向量数据库基础概念

LLM的向量通常是在数据经过Embedding模型后所得到的。由此产生大量的向量数据，而存储向量数据的数据库就是向量数据库

在这里插入图片描述
向量数据库的工作流程可概括为以下几个步骤：

向量化：使用嵌入模型将文本等数据转化为向量
索引构建：使用HNSW等算法构建高效检索索引
向量存储：将向量与原始数据元信息一起存储
相似性检索：基于距离计算（如余弦相似度、欧氏距离）找到最相似的向量
结果匹配：返回相似向量对应的原始数据

向量数据库之所以能实现高效检索，关键在于其高效的索引与搜索机制，举例百万的向量存储在向量数据库中，当用户输入时候首先进行索引构建得到topk个向量，而不是直接对百万个向量进行相似度计算。向量数据库中采用的索引技术为如下：

层次化可导航小世界(HNSW)：构建一种类似"快捷通道"的多层图结构，使搜索可以先在高层快速跳跃，再在低层精确定位，显著减少需要比较的向量数量。
乘积量化(PQ)：通过将高维向量分解并压缩成更小的子向量码本，大幅降低内存占用和计算复杂度，同时保留向量的核心语义特征。
局部敏感哈希(LSH)：巧妙地将相似向量映射到相同的"桶"中，使系统只需比较有限范围内的候选项，而非整个数据集。

主流向量数据库对比

目前市场上的向量数据库大致可分为两类：专用向量数据库和传统数据库的向量扩展。如图左侧板块是专用向量数据库，右侧是传统数据库的拓展。
在这里插入图片描述

Chroma：适合快速原型开发、中小规模项目、简单部署要求
Milvus：适合企业级应用、大规模项目、高并发场景、需要分布式部署

本文会重点分析两款热门的专用开源向量数据库：
chroma
Milvus

Chroma

Chroma是一款AI原生的开源向量数据库，特点是简单易用。
使用方式：pip install Chroma

核心优势：

框架集成：与LangChain、LlamaIndex等框架无缝对接
适合场景：千万级别向量的中小型项目

基本用法示例：

import chromadb

# 创建客户端
client = chromadb.Client()

# 创建集合
collection = client.create_collection(
    name="documents",
    embedding_function=embedding_model  # 指定向量化模型
)

# 添加文档
collection.add(
    documents=["文档内容..."],
    ids=["doc1"],
    metadatas=[{"category": "finance"}]  # 元数据用于后期过滤
)

# 查询相似文档
results = collection.query(
    query_texts=["用户问题"],
    n_results=3,
    where={"category": "finance"}  # 元数据过滤
)

Milvus

Milvus是一款高性能、分布式的云原生向量数据库,功能更强大，更适合大规模应用。本地部署支持百万级别查询，服务端部署支持亿级别查询。还支持GPU加速查询
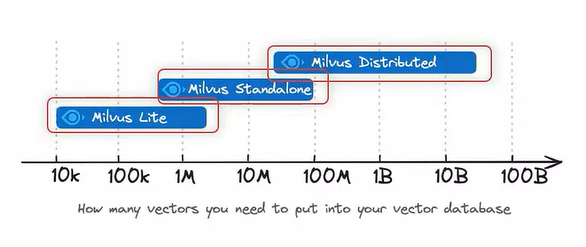
在这里插入图片描述

基本用法示例：

from pymilvus import connections, Collection, FieldSchema, CollectionSchema, DataType

# 连接Milvus服务器
connections.connect("default", host="localhost", port="19530")

# 需要使用FieldSchema，来声明字段
fields = [
    FieldSchema(name="id", dtype=DataType.INT64, is_primary=True),
    FieldSchema(name="embedding", dtype=DataType.FLOAT_VECTOR, dim=1536),
    FieldSchema(name="metadata", dtype=DataType.JSON)
]
schema = CollectionSchema(fields=fields)

# 创建集合
collection = Collection(name="documents", schema=schema)

# 创建索引
index_params = {
    "index_type": "IVF_FLAT",
    "metric_type": "L2",
    "params": {"nlist": 1024}
}
collection.create_index("embedding", index_params)

# 添加数据
collection.insert([
    [1],  # id
    [[0.1, 0.2, ..., 0.3]],  # 向量
    [{"category": "finance"}]  # 元数据
])

# 加载集合并查询
collection.load()
results = collection.search(
    data=[[0.1, 0.2, ..., 0.3]],
    anns_field="embedding",
    param={"metric_type": "L2"},
    limit=3,
    expr="metadata.category == 'finance'"  # 元数据过滤
)