周志华《机器学习》西瓜书-第十章-习题

周志华《机器学习》西瓜书第十章的习题答案较少，只找到了两篇，见文末链接，以下是个人对这章的习题的理解，如有问题，欢迎指正。其中第一题和第六题网上答案较多，不再重复。

10.2关于err,err*不等式的证明

这里|y|是类的数量。

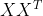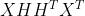10.3“中心化”，常见的方法是将协方差矩阵转换为，其中H=。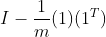

中心化，即，X为dxm维，，

1为mx1维的全1列向量，，

，其中，是dx1维的。

所以有 。

10.4由中心化后的样本矩阵X的奇异值分解代替，试讲述原因。

等价：X的奇异值分解为，，而，，因此。对特征分解，有，只需P=U即可。

另外，用奇异值分解代替特征分解，节省了计算和存储的成本，且计算精度较高。

10.5正交、非正交投影矩阵用于降维的优缺点。

正交：属性间独立，维数更低，耦合性小。
非正交：保留了属性间的联系。
正交投影矩阵还满足 最佳逼近定理。

10.7核化线性降维和流形学习之间的联系和优缺点。

联系：都是非线性降维。
KPCA：先升到高维，在高维中是线性的，再用PCA降维。有核方法的一切优势，但计算量较大，核函数难选。新样本值可直接带入。难以兼顾泛化性和效率.
流形学习：可在保持原结构的条件下降维，假设和近似条件较多（只是假设流形存在），解决了部分高维的问题，但不能总适合数据的特点，计算复杂度较高，分类能力较弱（如短路断路问题），低维的维度数难确定，新样本难带入，对噪声敏感，大部分问题目前仍在研究中。

10.8k近邻图和ε近邻图存在的短路和断路问题会给Isomap造成困扰,试设计一个方法缓解该问题。

k与ε联合使用；
网上有论文使用基于聚类的方法和基于优化拓扑结构的方法。

10.9试设计一个方法为新样本找到LLE降维后的低维坐标。

寻找k近邻——>根据式10.28计算wij——>用k近邻的zj和wij线性表示该新样本。

10.10试述如何确保度量学习产生的距离能满足距离度量的四条基本性质。

不是很理解这道题的意思，是不是要求M是半正定的？

参考文章

http://www.lunarnai.cn/2018/12/06/watermelon-chap-10/

https://blog.csdn.net/VictoriaW/article/details/78359362