ReLU函数详解及反向传播中的梯度求导

摘要

本文给出 ReLU 函数的定义, 并求解其在反向传播中的梯度

相关

配套代码, 请参考文章 :

Python和PyTorch对比实现ReLU函数及反向传播

系列文章索引 :
https://blog.csdn.net/oBrightLamp/article/details/85067981

正文

1. 定义

ReLU函数, 即线性整流函数(Rectified Linear Unit), 是神经网络结构中常用的非线性激活函数.
其定义如下:
$$ReLU(x)=\{\begin{array}{rr}0,& x⩽0\\ x,& x>0\end{array}$$

函数图像 :

2. 反向传播

ReLU 函数是逐个处理输入值的, 并不需要写成向量的形式.
但为了方便编程实现, 这里将其进行改编成向量的形式.

考虑一个输入向量 x , 经 ReLU 函数变换后得到向量 r, 往前 forward 传播得到误差值 error (标量 e ), 求 e 对 x 的梯度.
$$\begin{gathered} x=(x_1,x_2,x_3,\cdots ,x_k) \\ r=ReLU(x) \\ e=forward(r) \end{gathered}$$

求解过程 :
$$\begin{gathered} \frac{d{r}_i}{d{x}_i}=\{\begin{array}{rr}0,& x_i⩽0\\ 1,& x_i>0\end{array} \\ m=(\frac{\partial r_1}{\partial x_1},\frac{\partial r_2}{\partial x_2},\frac{\partial r_3}{\partial x_3},\cdots ,\frac{\partial r_k}{\partial x_k}) \\ \nabla e_{(r)}=(\frac{\partial e}{\partial r_1},\frac{\partial e}{\partial r_2},\frac{\partial e}{\partial r_3},\cdots ,\frac{\partial e}{\partial r_k}) \\ \frac{\partial e}{\partial x_i}=\frac{\partial e}{\partial r_i}\frac{\partial r_i}{\partial x_i} \\ \nabla e_{(x)}=(\frac{\partial e}{\partial x_1},\frac{\partial e}{\partial x_2},\frac{\partial e}{\partial x_3},\cdots ,\frac{\partial e}{\partial x_k})=\nabla e_{(r)}\odot m \end{gathered}$$

向量 $\nabla e_{(r)}$ 由上游负责计算, 是已知的, x 确定时 m 也是已知的, $\odot$ 表示元素积, 即同位元素相乘.

3. ReLU 函数的作用

为了理解 ReLU 函数的作用, 我们引入一种在电子电路中广泛应用的电子元器件 :

二极管 (英语：Diode)，电子元件当中, 一种具有两个电极的装置, 只允许电流由单一方向流过, 用于整流电路，可以把交流电变换成脉动的直流电, 即整流二极管 (rectifier diode).

上图左边是整流二极管的特性曲线, 右边是整流二极管在电路图中的表示符号.
左边$△U$部分是击穿电压, 很容易烧毁二极管, 不是整流二极管的正常工作范围.
可以看到, 正常工作范围的特性曲线和 ReLU 函数的图像非常相似.

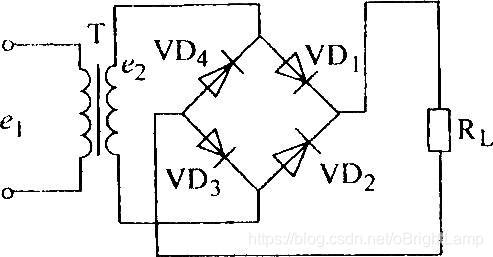
上图是常见的整流电路, 利用电流只能在二极管中单向传播的特性, 通过四只二极管组合, 就可以很方便将来自 T 的交流电转换为$R_L$使用的直流电.
使用 Python 模拟整流电路 :

import numpy as np
import matplotlib.pyplot as plt


def relu(signal):
    return np.maximum(0, signal)


def relu_reverse(signal):
    return -np.minimum(0, signal)


x = np.linspace(-10, 10, 2000)
y = np.sin(x)

plt.axhline(color="black")
plt.axvline(color="black")
plt.plot(x, y)
plt.show()

y = relu(y) + relu_reverse(y)

plt.axhline(color="black")
plt.axvline(color="black")
plt.plot(x, y)
plt.show()

整流前 :

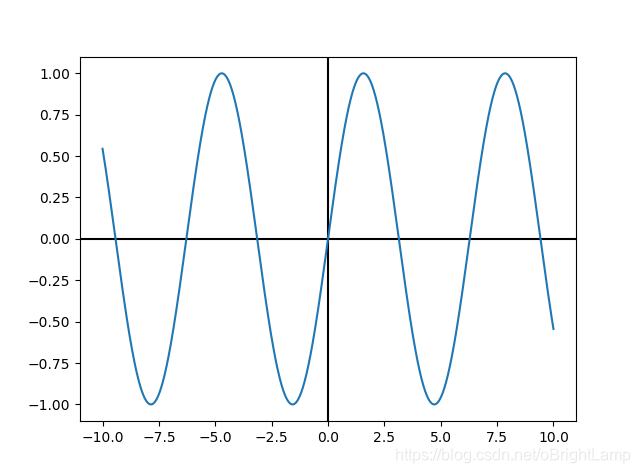
整流后 :

可以看到, 经过整流后, 所有的反向信号都调整为正向信号了.

4. ReLU + 线性组合

在常见的神经网络结构中, ReLU 经常和线性变换一起使用.

$$\begin{gathered} a_i=a_i{x}_i+b_i \\ y=\sum _{k=1}^{k}ReLU(a_i) \end{gathered}$$

import numpy as np
import matplotlib.pyplot as plt


def relu(signal):
    return np.maximum(0, signal)


x = np.linspace(-10, 10, 2000)

b1 = 0.00 * np.pi
b2 = 0.25 * np.pi
b3 = 0.50 * np.pi
b4 = 0.75 * np.pi
b5 = 1.00 * np.pi
b6 = 1.25 * np.pi
b7 = 1.50 * np.pi
b8 = 1.75 * np.pi

y1 = np.sin(x + b1)
y2 = np.sin(x + b2)
y3 = np.sin(x + b3)
y4 = np.sin(x + b4)
y5 = np.sin(x + b5)
y6 = np.sin(x + b6)
y7 = np.sin(x + b7)
y8 = np.sin(x + b8)

y = relu(y1) + relu(y2) + relu(y3) + relu(y4)
y += relu(y5) + relu(y6) + relu(y7) + relu(y8)

plt.plot(x, y)
plt.axhline(color="black")
plt.axvline(color="black")
plt.show()

只需要有限的几个 ReLU 进行组合, 就可以将交流信号调整到不错的直流信号.

ReLU 函数虽然很简单, 但和其他函数组合后却有神奇的非线性拟合能力.