Probabilistic Machine Learning：Introduction 概率机器学习：简介- 3 概率：多元模型（1）-page 107-136/858

3.1 多个随机变量的联合分布

在本节中，我们讨论衡量一个或多个变量彼此依赖程度的各种方法。

3.1.1 协方差

两个随机变量X和Y之间的协方差衡量了X和Y之间的（线性）相关程度。协方差的定义如下：

[ \text{Cov}[X, Y] = E\left[(X - E[X])(Y - E[Y])\right] = E[XY] - E[X]E[Y] ]

如果x是一个D维的随机向量，其协方差矩阵定义为以下对称、半正定矩阵：

[ \text{Cov}[x] = E\left[(x - E[x])(x - E[x])^T\right] = \Sigma ]

[

\begin{bmatrix}
V[X_1] & \text{Cov}[X_1, X_2] & \ldots & \text{Cov}[X_1, X_D] \
\text{Cov}[X_2, X_1] & V[X_2] & \ldots & \text{Cov}[X_2, X_D] \
\vdots & \vdots & \ddots & \vdots \
\text{Cov}[X_D, X_1] & \text{Cov}[X_D, X_2] & \ldots & V[X_D]
\end{bmatrix}
]

由此得出一个重要的结果：

[ E[xx^T] = \Sigma + \mu\mu^T ]

另一个有用的结果是线性变换的协方差：

[ \text{Cov}[Ax + b] = A \text{Cov}[x] A^T ]

如Exercise 3.4所示。

两个随机向量之间的交叉协方差定义为：

[ \text{Cov}[x, y] = E\left[(x - E[x])(y - E[y])^T\right] ]

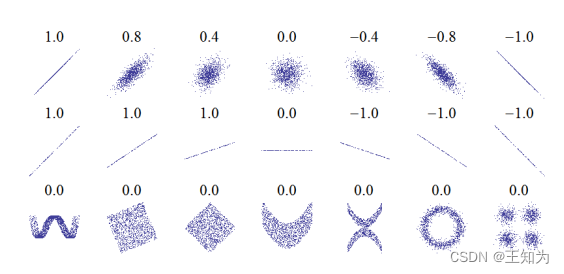
Figure 3.1: 几组（x, y）点集，每组的x和y的相关系数。请注意，相关系数反映了线性关系的噪声程度和方向（顶部行），但不反映该关系的斜率（中部行），也不反映许多非线性关系的方面（底部行）。 （注意：中央的图形具有0的斜率，但在这种情况下，相关系数未定义，因为Y的方差为零。）来源：https://en.wikipedia.org/wiki/Pearson_correlation_coefficient，获得Wikipedia作者Imagecreator的友善许可。

3.1.2 相关系数
协方差可以在负无穷到正无穷之间取值。有时使用一种归一化的度量，具有有限的下限和上限，更为方便。X和Y的（Pearson）相关系数定义为：
[ \rho, \text{corr}[X, Y] = \frac{\text{Cov}[X, Y]}{\sqrt{V[X] \cdot V[Y]}} ]
可以证明（练习3.2）(-1 \leq \rho \leq 1)。
还可以证明，(\text{corr}[X, Y] = 1)当且仅当Y = aX + b（其中a > 0）具有一些参数a和b，即X和Y之间存在线性关系（见练习3.3）。直观地，人们可能期望相关系数与回归线的斜率有关，即表达式Y = aX + b中的系数a。然而，正如我们在方程（11.27）中所示，实际上回归系数由(a = \text{Cov}[X, Y] / V[X])给出。在图3.1中，我们展示了相关系数对于强烈但是非线性关系可以为0的情况（与图6.6进行比较）。因此，更好的看待相关系数的方式是将其视为线性程度的度量（请参见correlation2d.ipynb以演示此思想）。
对于相关的随机变量向量x的情况，相关矩阵由以下形式给出：
[ \text{corr}(x) = \begin{bmatrix} 1 & \frac{E[(X_1-\mu_1)(X_2-\mu_2)]}{\sigma_1 \sigma_2} & \cdots & \frac{E[(X_1-\mu_1)(X_D-\mu_D)]}{\sigma_1 \sigma_D} \ \frac{E[(X_2-\mu_2)(X_1-\mu_1)]}{\sigma_2 \sigma_1} & 1 & \cdots & \frac{E[(X_2-\mu_2)(X_D-\mu_D)]}{\sigma_2 \sigma_D} \ \vdots & \vdots & \ddots & \vdots \ \frac{E[(X_D-\mu_D)(X_1-\mu_1)]}{\sigma_D \sigma_1} & \frac{E[(X_D-\mu_D)(X_2-\mu_2)]}{\sigma_D \sigma_2} & \cdots & 1 \end{bmatrix} ]
这可以更简洁地写成：
[ \text{corr}(x) = \left(\text{diag}(K_{xx})\right)^{-\frac{1}{2}} K_{xx} \left(\text{diag}(K_{xx})\right)^{-\frac{1}{2}} ]

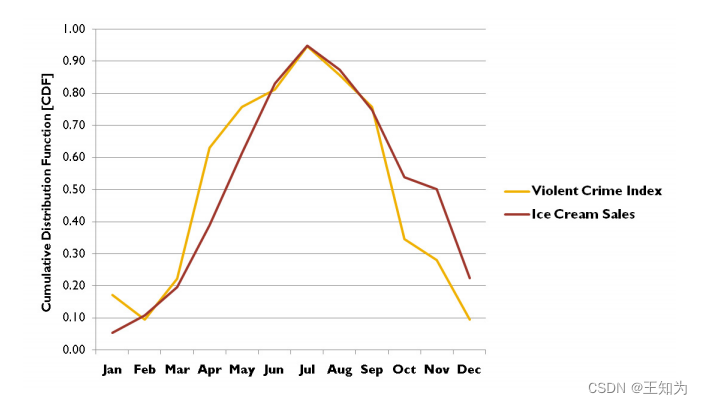
Figure 3.2: 因果无关时间序列之间的虚假相关性示例。冰淇淋消费（红色）和暴力犯罪率（黄色）随时间的变化。来源：http://icbseverywhere.com/blog/2014/10/the-logic-of-causal-conclusions/，获得Barbara Drescher的授权使用。

翻译

3.1 多维随机变量的联合分布

在本节中，我们讨论衡量一个或多个变量之间相互依赖的各种方式。

3.1.1 协方差

随机变量X和Y之间的协方差衡量了X和Y是（线性）相关的程度。协方差定义如下：

[ \text{Cov}[X, Y] = \mathbb{E}\left[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])\right] = \mathbb{E}[XY] - \mathbb{E}[X]\mathbb{E}[Y] ]

如果(x)是一个D维随机向量，它的协方差矩阵定义如下对称正半定矩阵：

[ \text{Cov}[x] = \mathbb{E}\left[(x - \mathbb{E}[x])(x - \mathbb{E}[x])^T\right] = \Sigma ]

[ = \begin{bmatrix} V[X_1] & \text{Cov}[X_1, X_2] & \ldots & \text{Cov}[X_1, X_D] \ \text{Cov}[X_2, X_1] & V[X_2] & \ldots & \text{Cov}[X_2, X_D] \ \vdots & \vdots & \ddots & \vdots \ \text{Cov}[X_D, X_1] & \text{Cov}[X_D, X_2] & \ldots & V[X_D] \end{bmatrix} ]

由此得到的重要结果是：

[ \mathbb{E}[xx^T] = \Sigma + \mu\mu^T ]

另一个有用的结果是线性变换的协方差：

[ \text{Cov}[Ax + b] = A\text{Cov}[x]A^T ]

详细内容可以参见练习3.4。

两个随机向量之间的交叉协方差定义为：

[ \text{Cov}[x, y] = \mathbb{E}\left[(x - \mathbb{E}[x])(y - \mathbb{E}[y])^T\right] ]

3.1.2 相关性

协方差可以取负无穷到正无穷的任意值。有时更方便使用一种标准化的测量方式，具有有限的下限和上限。(X)和(Y)之间的（Pearson）相关系数定义如下：

[ \rho = \text{corr}[X, Y] = \frac{\text{Cov}[X, Y]}{\sqrt{V[X]V[Y]}} ]

我们可以证明（练习3.2）(-1 \leq \rho \leq 1)。

我们还可以证明，(\text{corr}[X, Y] = 1)当且仅当(Y = aX + b)（其中(a > 0)）时，即X和Y之间存在线性关系（参见练习3.3）。直观上，人们可能期望相关系数与回归线的斜率有关，即表达式(Y = aX + b)中的系数a。然而，正如我们在方程（11.27）中所示，回归系数实际上由(a = \text{Cov}[X, Y] / V[X])给出。在图3.1中，我们展示了相关系数对于强但是非线性关系可能为零的情况（与图6.6进行比较）。因此，更好的看待相关系数的方式是将其视为一种线性程度度量（参见correlation2d.ipynb进行演示）。

对于相关变量的向量(x)，相关矩阵如下定义：

[ \text{corr}(x) = \begin{bmatrix} 1 & \frac{\mathbb{E}[(X_1-\mu_1)(X_2-\mu_2)]}{\sigma_1\sigma_2} & \ldots & \frac{\mathbb{E}[(X_1-\mu_1)(X_D-\mu_D)]}{\sigma_1\sigma_D} \ \frac{\mathbb{E}[(X_2-\mu_2)(X_1-\mu_1)]}{\sigma_2\sigma_1} & 1 & \ldots & \frac{\mathbb{E}[(X_2-\mu_2)(X_D-\mu_D)]}{\sigma_2\sigma_D} \ \vdots & \vdots & \ddots & \vdots \ \frac{\mathbb{E}[(X_D-\mu_D)(X_1-\mu_1)]}{\sigma_D\sigma_1} & \frac{\mathbb{E}[(X_D-\mu_D)(X_2-\mu_2)]}{\sigma_D\sigma_2} & \ldots & 1 \end{bmatrix} ]

可以更简洁地写成：

[ \text{corr}(x) = (\text{diag}(K_{xx}))^{-\frac{1}{2}} K_{xx} (\text{diag}(K_{xx}))^{-\frac{1}{2}} ]

其中(K_{xx}\[ K_{xx} = \Sigma = \mathbb{E}[(x - \mathbb{E}[x])(x - \mathbb{E}[x])^T] = R_{xx} - \mu\mu^T ]

其中( R_{xx} = \mathbb{E}[xx^T] )是自相关矩阵。

3.1.3 不相关不意味着独立

如果(X)和(Y)是独立的，即(p(X, Y) = p(X)p(Y))，那么(\text{Cov}[X, Y] = 0)，因此(\text{corr}[X, Y] = 0)。因此，独立蕴含不相关。然而，反之不成立：不相关不蕴含独立。例如，取(X \sim U(-1, 1))和(Y = X^2)。显然，(Y)依赖于(X)（事实上，(Y)由(X)唯一确定），然而我们可以证明（练习3.1）(\text{corr}[X, Y] = 0)。

图3.1展示了几个数据集，其中(X)和(Y)之间存在明显的依赖关系，但是相关系数为0。更一般地衡量随机变量之间依赖关系的指标是互信息，见第6.3节。只有在变量真正独立时，互信息才为零。

3.1.4 相关性不蕴含因果关系

众所周知，“相关性不蕴含因果关系”。例如，考虑图3.2。在红色中，我们绘制了(x_{1:T})，其中(x_t)是第(t)个月的冰淇淋销售量。在黄色中，我们绘制了(y_{1:T})，其中(y_t)是第(t)个月的暴力犯罪率。 （量值已重新缩放以使图形重叠。）我们看到这两个信号之间存在强烈的相关性。事实上，有时候会声称“吃冰淇淋会导致谋杀”[Pet13]。当然，这只是一种伪相关，由于一个隐藏的共同原因，即天气。炎热的天气增加了冰淇淋的销售，这是显而易见的原因。炎热的天气还会增加暴力犯罪，其原因正在激烈地辩论中，有些人声称是由于愤怒增加[And01]，而其他人声称仅仅是因为更多的人在户外[Ash18]，而大多数谋杀案发生在户外。

另一个著名的例子涉及出生率与鸟类（一种鸟）的存在之间的正相关。这导致了一个关于鸟类“送来婴儿”的都市传说[Mat00]。当然，相关性的真正原因更可能是隐藏的因素，例如生活水平的提高，从而有更多的食物。在[Vig15]中可以找到更多有趣的这类伪相关的例子。

这些例子作为一个“警告”，我们不应将(x)对(y)的预测能力视为(x)导致(y)的指标。

3.1.5 辛普森悖论

辛普森悖论表明，在多个数据组中出现的统计趋势或关系，在这些组合并时可能会消失或反转符号。如果我们错误地以因果关系的方式解释对统计依赖性的声明，这将导致直观上令人费解的行为。

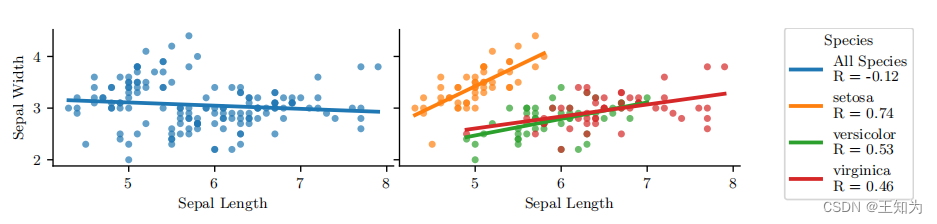
图3.3是辛普森悖论的一个例子，使用鸢尾花数据集进行说明。 （左侧）整体上，y（花萼宽度）随着x（花萼长度）减小而减小。 （右侧）在每个组内，y随着x的增加而增加。 通过simpsons_paradox.ipynb生成。

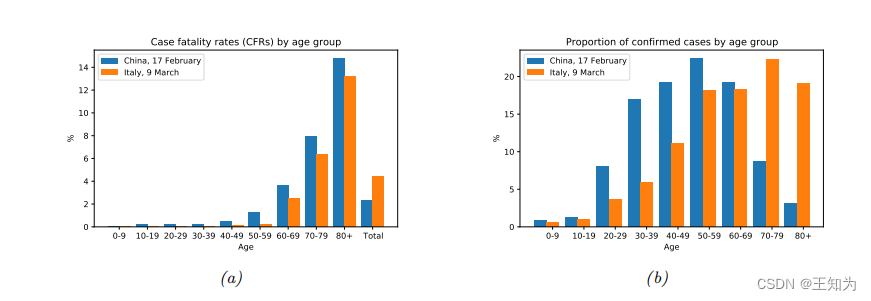
Figure 3.4: 利用COVID-19说明辛普森悖论，(a) 意大利和中国按年龄组分的病死率 (CFR)，以及按年龄组分的总体病死率（“Total”，最后一对条形图），截至报告时间（参见图例）。 (b) 在(a)中包括的所有确诊病例在每个年龄组内的比例。来自[KGS20]的第1图。经Julius von Kügelgen的友好许可使用。

3.2.1 定义
多元正态分布（MVN）的密度由以下定义：
[ N (y|\mu, \Sigma) = \frac{1}{(2\pi)^{{D/2}|\Sigma|}{1/2}} \exp\left( -\frac{1}{2}(y - \mu)^T \Sigma^{-1} (y - \mu) \right) ]
其中 (\mu = E [y] \in \mathbb{R}^D) 是均值向量，(\Sigma = Cov [y]) 是 (D \times D) 协方差矩阵，定义如下：
[ Cov [y] = E \left[ (y - E [y])(y - E [y])^T \right] ]
[ = \begin{bmatrix} V [Y_1] & Cov [Y_1, Y_2] & \dots & Cov [Y_1, Y_D] \ Cov [Y_2, Y_1] & V [Y_2] & \dots & Cov [Y_2, Y_D] \ \vdots & \vdots & \ddots & \vdots \ Cov [Y_D, Y_1] & Cov [Y_D, Y_2] & \dots & V [Y_D] \end{bmatrix} ]
其中
[ Cov [Y_i, Y_j] = E \left[ (Y_i - E [Y_i])(Y_j - E [Y_j]) \right] = E [Y_i Y_j] - E [Y_i] E [Y_j] ]
而 (V [Y_i] = Cov [Y_i, Y_i])。从方程（3.12）得到一个重要的结果：
[ E [yy^T] = \Sigma + \mu \mu^T ]

方程（3.11）中的标准化常数 (Z = (2\pi)^{{D/2}|\Sigma|}{1/2}) 只是确保概率密度函数积分为1的因子（见练习3.6）。

在二维情况下，MVN称为双变量高斯分布。其概率密度函数可以表示为 (y \sim N(\mu, \Sigma))，其中 (y \in \mathbb{R}^2)，(\mu \in \mathbb{R}^2) 且
[\Sigma = \begin{bmatrix} \sigma_1^2 & \sigma_{12} \ \sigma_{21} & \sigma_2^2 \end{bmatrix} = \begin{bmatrix} \sigma_1^2 & \rho\sigma_1\sigma_2 \ \rho\sigma_1\sigma_2 & \sigma_2^2 \end{bmatrix}]

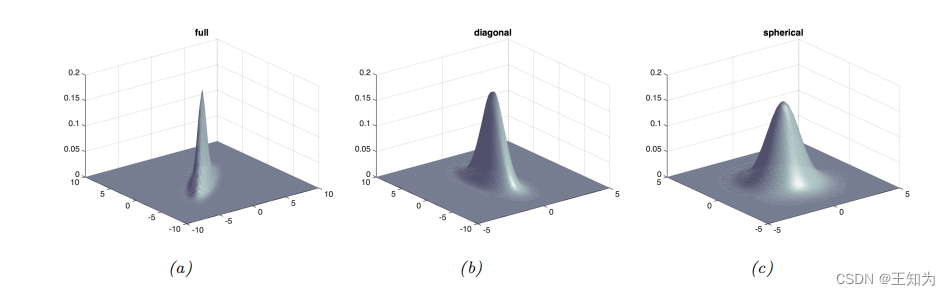
Figure 3.5: 二维高斯密度的可视化，作为表面绘图展示。 (a) 使用完整协方差矩阵的分布可以以任何角度定向。 (b) 使用对角协方差矩阵的分布必须平行于坐标轴。 © 使用球形协方差矩阵的分布必须具有对称形状。 由 gauss_plot_2d.ipynb 生成。

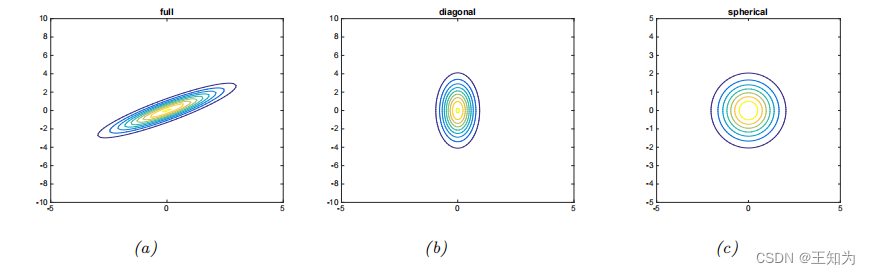
Figure 3.6: 二维高斯密度的可视化，以常数概率密度的等高线表示。 (a) 完整协方差矩阵具有椭圆形轮廓。 (b) 对角协方差矩阵是一个与坐标轴对齐的椭圆。 © 球形协方差矩阵具有圆形轮廓。 由 gauss_plot_2d.ipynb 生成。

Figure 3.5和Figure 3.6绘制了2D中三种不同协方差矩阵的一些MVN密度。完整的协方差矩阵具有D(D + 1)/2个参数，其中我们除以2是因为Σ是对称的。（椭圆形状的原因在第7.4.4节中解释，其中我们讨论二次型的几何形状。）对角协方差矩阵有D个参数，并且在非对角线项上有0。球形协方差矩阵，也称为各向同性协方差矩阵，具有Σ = σ2
ID的形式，因此只有一个自由参数，即σ2。

3.2.2 Mahalanobis距离
在这一节中，我们尝试对多维高斯概率密度的几何形状有一些了解。为了做到这一点，我们将考虑常数（对数）概率水平集的形状。
在特定点y处的对数概率由以下公式给出：
log p(y|µ, Σ) = −12(y − µ)TΣ−1(y − µ) + const (3.19)
对y的依赖性可以用Mahalanobis距离∆表示，其平方定义如下：
∆2 ,(y − µ)TΣ−1(y − µ) (3.20)
因此，常数（对数）概率的轮廓等于常数Mahalanobis距离的轮廓。
为了深入了解常数Mahalanobis距离的轮廓，我们利用了Σ和因此Λ = Σ−1
都是正定矩阵（根据假设）。考虑Σ的以下特征分解（第7.4节）：Σ =DXd=1λduduTd(3.21)我们可以类似地写出Σ−1 =DXd=11λduduTd(3.22)
让我们定义zd，uTd(y − µ)，因此z = U(y − µ)。然后，我们可以重新写Mahalanobis距离如下：
(y − µ)TΣ−1(y − µ) = (y − µ)T DXd=11λduduTd!(y − µ) (3.23)
=DXd=11λd(y − µ)TuduTd(y − µ) =DXd=1z2dλd(3.24)
正如我们在第7.4.4节中讨论的那样，这意味着我们可以将Mahalanobis距离解释为在新坐标框架z中的欧几里德距离，在这个坐标框架中，我们通过U旋转y并通过Λ进行缩放。

图3.7: 利用MVN进行数据插补的示例。 (a) 尺寸为N = 10，D = 8的数据矩阵可视化。空白条目表示缺失（未观测到的）。蓝色表示正值，绿色表示负值。方块的面积与数值成比例。（这被称为Hinton图，以Geoff Hinton，一位著名的机器学习研究者，命名。）(b) 真实数据矩阵（隐藏的）。© 基于该行部分观测数据使用真实模型参数的后验预测分布的均值。由gauss_imputation_known_params_demo.ipynb生成。

3.3 线性高斯系统 *
在第3.2.3节中，我们基于无噪声的观测条件来推断高斯随机向量的隐藏部分的后验分布。在本节中，我们扩展这种方法来处理带有噪声观测的情况。
设 ( z \in \mathbb{R}^L ) 为一组未知值，( y \in \mathbb{R}^D ) 为 ( z ) 的一些带噪声测量。我们假设这些变量之间存在以下联合分布：
[ p(z) = \mathcal{N}(z|\mu_z, \Sigma_z) ]
[ p(y|z) = \mathcal{N}(y|Wz + b, \Sigma_y) ]
其中 ( W ) 是一个大小为 ( D \times L ) 的矩阵。这是线性高斯系统的一个示例。
相应的联合分布 ( p(z, y) = p(z)p(y|z) ) 是一个 ( L + D ) 维的高斯分布，其均值和协方差矩阵分别为
[ \mu = \begin{bmatrix} W\mu_z + b \ \mu_z \end{bmatrix} ]
[ \Sigma = \begin{bmatrix} \Sigma_z & \Sigma_{zW} \ \Sigma_{Wz} & \Sigma_y \end{bmatrix} ]

通过将Gaussian conditioning公式（Equation 3.28）应用于联合分布 ( p(y, z) )，我们可以计算后验分布 ( p(z|y) )，如下所述。这可以解释为在从潜在变量到观测数据的生成模型中反转 ( z \rightarrow y ) 箭头。

【续】

[ \left[ \begin{array}{c} \mu_{z|y} \ \mu_{y|z} \end{array} \right] = \left[ \begin{array}{c} \Sigma_{z|y} \left( W^T \Sigma_y^{-1} (y - b) + \Sigma_z^{-1} \mu_z \right) \ \Sigma_{y|z} \left( \Sigma_z^{-1} \mu_z - W^T \Sigma_y^{-1} b \right) \end{array} \right] ]

然后通过专注于相关的项，可以得到条件分布 ( p(z|y) )：

[ p(z|y) = N(\mu_{z|y}, \Sigma_{z|y}) ]

其中

[ \Sigma_{z|y} = \Sigma_z - \Sigma_{zy} \Sigma_{y|z} ]
[ \mu_{z|y} = \mu_z + \Sigma_{zy} \Sigma_{y|z} (\Sigma_y^{-1} (y - b) - W \mu_z) ]

这结束了条件分布 ( p(z|y) ) 的推导。

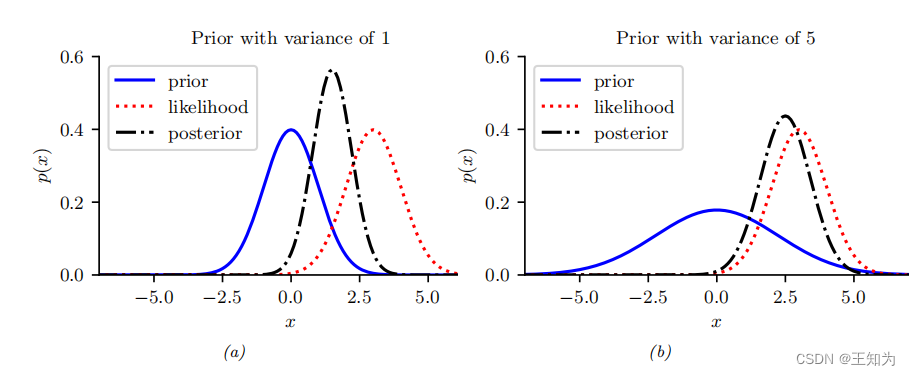
Figure 3.8: 给定一个噪声观测 (y = 3) 的 (z) 推断。 (a) 强先验 (N(0, 1))。后验均值向先验均值“收缩”，即0。 (b) 弱先验 (N(0, 5))。后验均值类似于极大似然估计。 生成自 gauss_infer_1d.ipynb。

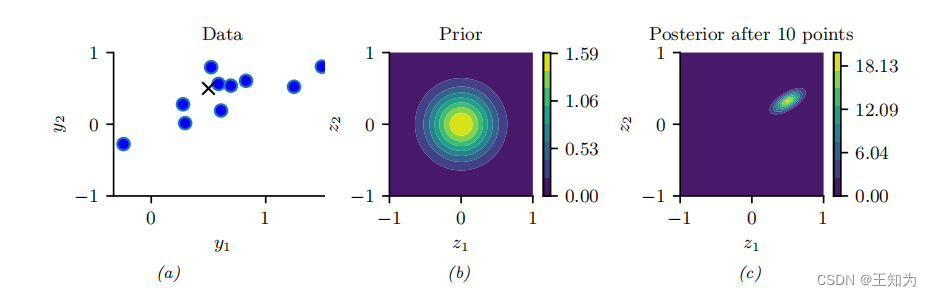
Figure 3.9: 2D 高斯随机向量 (z) 的贝叶斯推断示例。 (a) 数据由 (y_n \sim N(z, \Sigma_y)) 生成，其中 (z = [0.5, 0.5]^T)，(\Sigma_y = 0.1\begin{bmatrix}2 & 1 \ 1 & 1\end{bmatrix})。我们假设传感器噪声协方差 (\Sigma_y) 已知，但 (z) 是未知的。黑色十字表示 (z)。 (b) 先验分布为 (p(z) = N(z|0, 0.1I_2))。 © 在观察到10个数据点后显示后验分布。 生成自 gauss_infer_2d.ipynb。

3.3.5 示例：传感器融合
在本节中，我们扩展了第3.3.4节，考虑了具有不同可靠性的多个传感器提供的多个测量的情况。也就是说，模型具有以下形式：
[ p(z, y) = p(z) \prod_{m=1}^{M} \prod_{n=1}^{N_m} N(y_{n,m} | z, \Sigma_m) ]

其中 ( M ) 是传感器（测量设备）的数量，( N_m ) 是传感器 ( m ) 的观测数量，( y = y_{1:N,1:M} \in \mathbb{R}^K )。我们的目标是将这些证据结合起来，计算 ( p(z|y) )。这称为传感器融合。

我们现在给出一个简单的例子，其中只有两个传感器，因此 ( y_1 \sim N(z, \Sigma_1) ) 和 ( y_2 \sim N(z, \Sigma_2) )。在图形上，我们可以将这个例子表示为 ( y_1 \leftarrow z \rightarrow y_2 )。我们可以将 ( y_1 ) 和 ( y_2 ) 合并成一个单独的向量 ( y )，因此模型可以表示为 ( z \rightarrow [y_1, y_2] )，其中 ( p(y|z) = N(y|Wz, \Sigma_y) )，其中 ( W = [I; I] ) 和 ( \Sigma_y = [\Sigma_1, 0; 0, \Sigma_2] ) 是块结构矩阵。然后，我们可以应用高斯贝叶斯规则来计算 ( p(z|y) )。

图3.10(a)给出了一个2D示例，其中我们设置 ( \Sigma_1 = \Sigma_2 = 0.01I_2 )，因此两个传感器的可靠性相同。在这种情况下，后验均值位于两个观测 ( y_1 ) 和 ( y_2 ) 之间。在图3.10(b)中，我们设置 ( \Sigma_1 = 0.05I_2 ) 和 ( \Sigma_2 = 0.01I_2 )，因此传感器2比传感器1更可靠。在这种情况下，后验均值更接近于 ( y_2 )。在图3.10©中，我们设置
[ \Sigma_1 = 0.01 \begin{bmatrix} 10 & 1 \ 1 & 1 \end{bmatrix}, \quad \Sigma_2 = 0.01 \begin{bmatrix} 1 & 1 \ 1 & 10 \end{bmatrix} ]
因此传感器1在第二个分量（垂直方向）更可靠，传感器2在第一个分量（水平方向）更可靠。在这种情况下，后验均值使用了 ( y_1 ) 的垂直分量和 ( y_2 ) 的水平分量。

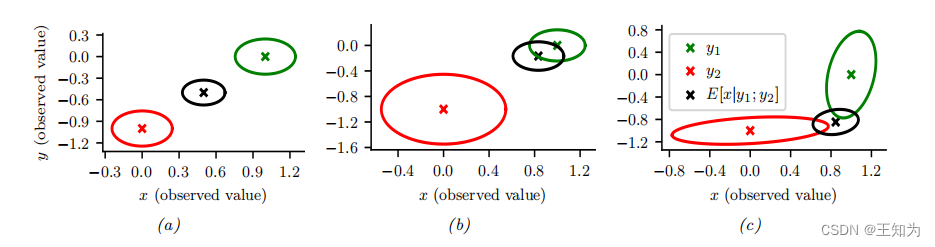
Figure 3.10: 我们观察到 ( y_1 = (0, -1) )（红十字）和 ( y_2 = (1, 0) )（绿十字），并估计 ( E [z|y_1, y_2] )（黑十字）。 (a) 传感器同等可靠，因此后验均值估计位于两个圆之间。 (b) 传感器2更可靠，因此估计更向绿色圆移动。 © 传感器1在垂直方向更可靠，传感器2在水平方向更可靠。 估计是对两个测量的适当组合。 由 sensor_fusion_2d.ipynb 生成。

3.4 指数家族 *
在本节中，我们定义了指数家族，它包括许多常见的概率分布。指数家族在统计学和机器学习中起着关键作用。在本书中，我们主要将其用于广义线性模型的背景下，这将在第12章中讨论。在本书的后续部分，[Mur23]中，我们还将看到指数家族的更多应用。

3.4.1 定义
考虑一个由参数 η ∈ ℝ^K 参数化的概率分布族，其固定支持集为 Y^D ⊆ ℝ^D。如果分布 p(y|η) 的密度可以写成以下形式，则我们称之为指数家族：

p(y|η) ∝ Z(1/η)h(y) exp[η^T T(y) - A(η)]

其中 h(y) 是一个比例常数（也称为基础度量，通常为1），T(y) ∈ ℝ^K 是充分统计量，η 是自然参数或典型参数，Z(η) 是分区函数，A(η) = log Z(η) 是对数分区函数。可以证明 A 是凸函数，定义域为凸集 Ω，{η ∈ ℝ^K : A(η) < ∞}。
如果自然参数彼此独立，那将更方便。正式地说，如果不存在 η ∈ ℝ^K \ {0} 使得 η^T T(y) = 0，则指数家族是最小的。在多项式分布的情况下，这个条件可能会被违反，因为参数存在总和为一的约束；然而，可以通过使用 K − 1 个独立参数对分布进行重新参数化，如下所示。

方程（3.71）可以通过定义 η = f(φ)，其中 φ 是另一组可能较小的参数，来进行泛化。在这种情况下，分布采用以下形式：

p(y|φ) = h(y) exp[f(φ)^T T(y) - A(f(φ))]

如果从 φ 到 η 的映射是非线性的，则称之为弯曲指数家族。如果 η = f(φ) = φ，模型被称为典型形式。如果此外还有 T(y) = y，则称之为自然指数家族或 NEF。在这种情况下，它可以写成：

p(y|η) = h(y) exp[η^T y - A(η)]

3.4.2 示例
作为一个简单的示例，让我们考虑伯努利分布。我们可以将其写成指数家族形式：

Ber(y|µ) = µ^y(1 − µ)^(1−y)
= exp[y log(µ) + (1 − y) log(1 − µ)]
= exp[T(y)^T η]

其中 T(y) = [I(y = 1), I(y = 0)]，η = [log(µ), log(1 − µ)]，µ 是均值参数。然而，由于特征之间存在线性依赖，这是一个过度完备的表示。我们可以如下看待：

1^T T(y) = I(y = 0) + I(y = 1) = 1

如果表示是过度完备的，则 η 就不是唯一可识别的。通常使用最小表示，这意味着与分布关联的 η 是唯一的。在这种情况下，我们可以定义：

Ber(y|µ) = exp[y log(µ / (1 − µ)) + log(1 − µ)]

我们可以通过定义以下指数家族形式来将其放入：

η = log(µ / (1 − µ))
T(y) = y
A(η) = -log(1 − µ) = log(1 + e^η)
h(y) = 1

我们可以使用自然参数 η 从典型参数 µ 中恢复均值参数，方法是：

µ = σ(η) = 1 / (1 + e^(-η))

其中我们识别出了 logistic（sigmoid）函数。

有关更多示例，请参阅本书的续篇 [Mur23]。

“Probabilistic Machine Learning: An Introduction” 草稿。2023年6月22日

3.4.3 对数分区函数是累积生成函数
一个分布的第一和第二阶累积是其均值 E[Y] 和方差 V[Y]，而第一和第二阶矩是 E[Y] 和 E[Y^2]。我们也可以计算更高阶的累积（和矩）。指数家族的一个重要性质是对数分区函数的导数可用于生成充分统计的所有阶累积。特别地，第一和第二阶累积为：

∇A(η) = E[T(y)]
∇^2A(η) = Cov[T(y)]

从上面的结果中，我们看到 Hessian 矩阵是正定的，因此 A(η) 在 η 上是凸的。由于对数似然具有 log p(y|η) = η^T T(y) − A(η) + 常数的形式，我们看到这是凹的，因此最大似然估计有一个唯一的全局最大值。

3.4.4 指数家族的最大熵推导
假设我们想找到一个描述某些数据的分布 p(x)，其中我们只知道某些特征或函数 fk(x) 的期望值（Fk）：

∫ dx p(x) fk(x) = Fk

例如，f1 可能计算 x，f2 可能计算 x^2，使得 F1 是经验均值，F2 是经验二阶矩。我们对分布的先验信念是 q(x)。

为了正式化我们所说的“假设最少的次数”，我们

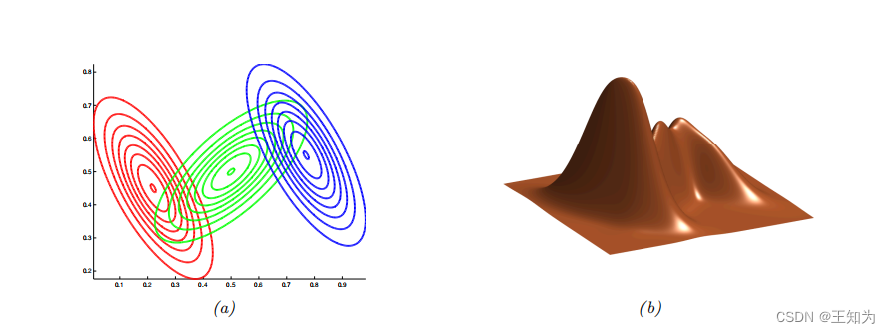
图 3.11：二维空间中的三个高斯混合分布。（a）展示混合中每个成分的等概率轮廓线。（b）整体密度的三维曲面图。改编自 [Bis06] 第2.23图。由 gmm_plot_demo.ipynb 生成。

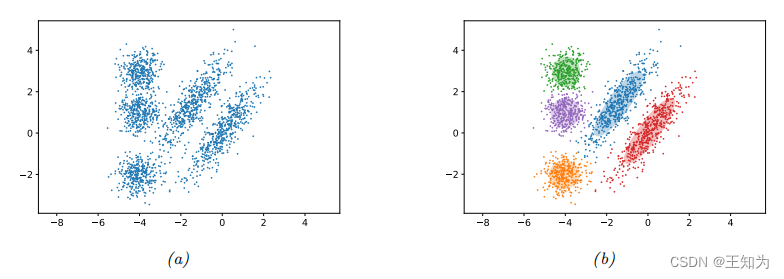
图 3.12：（a）二维数据示例。（b）使用 GMM 计算得到的 K = 5 个聚类的可能性。由 gmm_2d.ipynb 生成。

3.5.1 高斯混合模型
高斯混合模型（Gaussian Mixture Model，GMM），也称为高斯混合（Mixture of Gaussians，MoG），定义如下：
[ p(y|\theta) = \sum_{k=1}^{K} \pi_k \mathcal{N}(y | \mu_k, \Sigma_k) ]

在图 3.11 中，我们展示了二维高斯混合的密度示例，其中每个混合成分由不同的椭圆形轮廓表示。如果混合组件的数量足够多，GMM 可以逼近 (\mathbb{R}^D) 上的任何平滑分布。
GMM 经常用于对实值数据样本 (y_n \in \mathbb{R}^D) 进行无监督聚类。这在两个阶段内完成。首先，我们通过拟合模型（例如，通过计算 MLE ( \hat{\theta} = \arg\max \log p(D|\theta) )，其中 (D = {y_n : n = 1 : N})）来适应模型。我们讨论如何计算这个 MLE 在第 8.7.3 节。然后，我们将每个数据点 (y_n) 与离散的潜在变量 (z_n \in {1, \ldots, K}) 关联，该变量指定生成 (y_n) 所使用的混合组件或聚类的标识。这些潜在的标识是未知的，但我们可以使用贝叶斯规则计算它们的后验概率：
[ r_{nk} = p(z_n = k|y_n, \theta) = \frac{p(z_n = k|\theta)p(y_n|z_n = k, \theta)}{\sum_{k’=1}^{K} p(z_n = k’|\theta)p(y_n|z_n = k’, \theta)} ]
其中 (r_{nk}) 被称为聚类 (k) 对数据点 (n) 的责任。给定这些责任，我们可以计算最可能的聚类分配如下：
[ \hat{z}n = \arg\max_k r{nk} = \arg\max_k [\log p(y_n|z_n = k, \theta) + \log p(z_n = k|\theta)] ]
这被称为硬聚类（如果我们使用责任将每个数据点部分地分配到不同的聚类中，则被称为软聚类）。请参见图 3.12 以获取示例。
如果我们对 (z_n) 有均匀先验，并且使用球形高斯分布且 ( \Sigma_k = I)，那么硬聚类问题将简化为：
[ z_n = \arg\min_k ||y_n - \hat{\mu}_k||_2^2 ]
换句话说，我们将每个数据点分配给它距离最近的质心，由欧氏距离测量。这是 K 均值聚类算法的基础，我们将在第 21.3 节中讨论。

图 3.13：我们对二值化的 MNIST 数字数据拟合了一个由 20 个 Bernoulli 分布组成的混合模型。我们可视化了估计的聚类均值 ˆµk。每个图像上的数字表示估计的混合权重 ˆπk。在训练模型时未使用任何标签。由 mix_bernoulli_em_mnist.ipynb 生成。

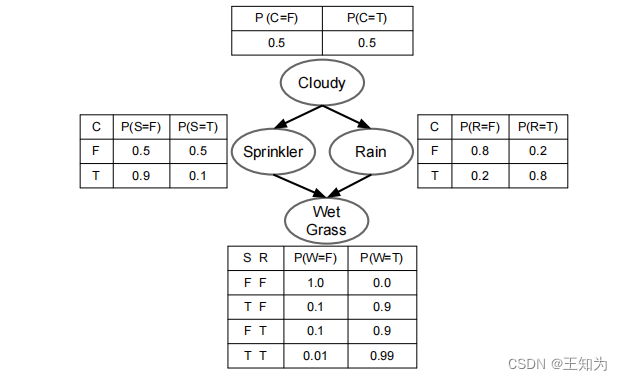
图 3.14：带有相应的二进制条件概率表的水花洒 PGM。T 和 F 代表真和假**

C) (3.105)

对于处理复杂系统的简单方法，我基本上了解两个原则：第一个是模块化原则，第二个是抽象原则。我是机器学习中计算概率的辩护者，因为我相信概率论通过因式分解和平均化以深刻而有趣的方式实现了这两个原则。充分利用这两种机制似乎是机器学习前进的道路。— Michael Jordan，1997年（引用自[Fre98]）。

我们已经介绍了一些简单的概率构建块。在第3.3节中，我们展示了一种将一些高斯构建块组合成高维分布p(y)的方法，即边缘p(y1)和条件p(y2|y1)。这个想法可以扩展到定义关于许多随机变量集合的联合分布。我们将做出的关键假设是一些变量在给定其他变量的条件下是独立的。我们将使用图形来表示我们的条件独立假设，如下面简要解释的那样（有关更多信息，请参见本书的续篇[Mur23]）。

3.6.1 表示

概率图模型或PGM是使用图形结构编码条件独立性假设的联合概率分布。当图形是有向无环图或DAG时，该模型有时被称为贝叶斯网络，尽管这些模型本质上与贝叶斯无关。

PGM的基本思想是图中的每个节点表示一个随机变量，每个边表示直接依赖关系。更准确地说，每个缺少边表示一种条件独立性。在DAG的情况下，我们可以按拓扑顺序编号节点（父节点在子节点之前），然后连接它们，以便每个节点在给定其父节点的情况下与所有其前驱节点独立：

[Y_i \perp \left( Y_{\text{pred}(i)} \setminus \text{pa}(i) \right) ,|, Y_{\text{pa}(i)}] (3.103)

其中(\text{pa}(i))是节点i的父节点，(\text{pred}(i))是节点i在排序中的前驱节点。 （这被称为有序马尔可夫性质。）因此，我们可以表示联合分布如下：

[p(Y_1:NG) = \prod_{i=1}^{NG} p(Y_i | Y_{\text{pa}(i)})] (3.104)

其中NG是图中的节点数。

3.6.1.1 示例：水喷淋网络

假设我们要模拟4个随机变量之间的依赖关系：C（是否为多云季节），R（是否下雨），S（是否开启喷水器）和W（草地是否湿润）。我们知道多云季节会增加下雨的可能性，因此我们添加了C → R的弧。我们知道多云季节会减少开启水喷淋器的可能性，因此我们添加了C → S的弧。最后，我们知道下雨或洒水器都可能导致草变湿润，因此我们添加了R → W和S → W的边缘。形式上，这定义了以下联合分布：

[p(C, S, R, W) = p© p(S|C) p(R|C) p(W|S, R, C)] (3.105)

对应的概率图模型如图3.14所示。在此图中：

• 节点表示随机变量：C（多云）、R（下雨）、S（洒水器）和W（湿润的草地）。
• 有向边表示直接依赖关系。例如，从C到R的箭头表示R直接依赖于C。
• 两个节点之间没有箭头表示条件独立性。例如，给定C，S和R是条件独立的，因此S和R之间没有箭头。

图中编码的条件独立性假设允许我们将联合分布分解为：

[ p(C, S, R, W) = p© p(S|C) p(R|C) p(W|S, R) ]

图形模型提供了一种直观的方式来表示复杂的概率关系和依赖关系。它们在机器学习、统计学和其他领域中被广泛应用于建模和推断。

3.6.1.2 示例：马尔可夫链

假设我们想要创建变长序列的联合概率分布，(p(y_{1:T}))。如果每个变量 (y_t) 表示来自具有 K 个可能值的词汇表的单词，因此 (y_t \in {1, . . . , K})，则得到的模型表示长度为 T 的可能句子的分布；这通常被称为语言模型。

根据概率的链式法则，我们可以表示任何 T 个变量的联合分布如下：

[ p(y_{1:T}) = p(y_1)p(y_2|y_1)p(y_3|y_2, y_1)p(y_4|y_3, y_2, y_1)… = \prod_{t=1}^{T} p(y_t|y_{1:t-1}) ]

不幸的是，用于表示每个条件分布 (p(y_t|y_{1:t-1})) 所需的参数数量随着 t 的增加呈指数级增长。然而，假设我们进行条件独立性假设，即未来 (y_{t+1:T}) 在给定现在 (y_t) 的情况下独立于过去 (y_{1:t-1})。这被称为一阶马尔可夫条件，如图3.15(a)所示。在这种假设下，我们可以将联合分布写为：

[ p(y_{1:T}) = p(y_1)p(y_2|y_1)p(y_3|y_2)p(y_4|y_3)… = p(y_1) \prod_{t=2}^{T} p(y_t|y_{t-1}) ]

这被称为马尔可夫链、马尔可夫模型或一阶自回归模型。函数 (p(y_t|y_{t-1})) 被称为转移函数、转移核或马尔可夫核。这只是在给定时间 t-1时状态的情况下，在时间 t 给定时间 t-1 时状态的条件分布，并且因此满足条件 (p(y_t|y_{t-1}) \geq 0) 以及 (\sum_{k=1}^{K} p(y_t = k|y_{t-1} = j) = 1)。我们可以将这个条件概率表（CPT）表示为一个随机矩阵，(A_{jk} = p(y_t = k|y_{t-1} = j))，其中每行的和为1。这被称为状态转移矩阵。我们假设此矩阵对于所有时间步都相同，因此模型被称为同质的、稳态的或时不变的。这是参数绑定的一个例子，因为相同的参数由多个变量共享。这个假设允许我们使用固定数量的参数来建模任意数量的变量。

一阶马尔可夫假设相当强。幸运的是，我们可以轻松将一阶模型推广到依赖于最后 M 个观测值的模型，从而创建一个 M 阶模型（记忆长度为 M）：

[ p(y_{1:T}) = p(y_{1:M}) \prod_{t=M+1}^{T} p(y_t|y_{t-M:t-1}) ]

这被称为 M 阶马尔可夫模型。例如，如果 (M = 2)，则 (y_t) 取决于 (y_{t-1}) 和 (y_{t-2})，如图3.15(b)所示。这被称为三元模型，因为它模型化了单词三元组的分布。如果我们使用 (M = 1)，则得到二元模型，它模型化了单词对的分布。

对于大词汇量，用于估计大 M 的 M-gram 模型的条件分布所需的参数数量可能会变得不可行。在这种情况下，我们需要在条件独立性之外进行其他假设。例如，我们可以假设 (p(y_t|y_{t-M:t-1})) 可以表示为低秩矩阵，或者用某种神经网络表示。这被称为神经语言模型。有关详细信息，请参见第15章。

3.6.2 推断

PGM定义了一个联合概率分布。因此，我们可以使用边际化和条件规则来计算对于任何变量 i 和 j 的 p(Y_i|Y_j = y_j)。执行此计算的有效算法在本书的续篇[Mur23]中有所讨论。

例如，考虑图3.14中的水喷淋示例。我们对下雨的先验信念是 (p(R = 1) = 0.5)。如果我们看到草地是湿润的，那么我们对下雨的后验信念会变成 (p(R = 1|W = 1) = 0.7079)。现在假设我们还注意到水喷淋器被打开了：我们对下雨的信念会下降到 (p(R = 1|W = 1, S = 1) = 0.3204)。一些观察的多因素负面相互作用称为解释偏效应，也被称为伯克森悖论。 （有关重现这些计算的代码，请参见sprinkler_pgm.ipynb。）

3.6.3 学习

如果 CPD 的参数是未知的，我们可以将它们视为额外的随机变量，将它们添加为图的节点，然后将它们视为要推断的隐藏变量。图3.16(a)