【笔记】从物理模型到Sigmoid函数，从Sigmoid函数到广义线性模型

最新推荐文章于 2024-07-18 16:00:59 发布

808130260

最新推荐文章于 2024-07-18 16:00:59 发布

阅读量1k

点赞数 1

分类专栏： python/机器学习

本文链接：https://blog.csdn.net/orangeOrangeRed/article/details/109853235

版权

python/机器学习专栏收录该内容

19 篇文章

订阅专栏

Sigmod 笔记

一、从物理模型到Sigmoid函数
二、从sigmoid函数到指数族分布
三、Sigmoid 激活函数
- sigmoid激活函数
- 双曲正切激活函数

一、从物理模型到Sigmoid函数

1. Ising模型

Ising模型的提出最初是为了解释铁磁物质的相变。即磁铁在加热到一定临界温度上下出现有磁性和无磁性两相的转变。

Ising模型假设:

铁磁物质是由一堆规则排列的小磁针构成，每个磁针只有上下两个方向（自旋） $s_i=\{+1, -1\}$ 。
相邻的小磁针之间通过能量约束发生相互作用。

如果将小磁针比喻成神经元细胞，向上向下的状态比喻成神经元的激活与抑制，小磁针的相互作用比喻成神经元之间的信号传导，那么，Ising模型的变种还可以用来建模神经网络系统，从而搭建可适应环境、不断学习的机器（Hopfield网络或Boltzmann机）。

同时又会由于环境热噪声的干扰而发生磁性的随机转变（上变为下或反之）。涨落的大小由关键的温度参数T决定。
- 温度越高，随机涨落干扰越强，小磁针越容易发生无序而剧烈地状态转变，从而让上下两个方向的磁性相互抵消，整个系统消失磁性；（相邻节点影响小）
- 如果温度很低，则小磁针相对宁静，系统处于能量约束高的状态,大量的小磁针方向一致,铁磁系统展现出磁性。（相邻节点影响大）
在村民的比喻中,温度相当于村民进行观点选择的自由程度，温度越高，村民选择观点越随机(变化快)，而不受自己周围邻居的影响；否则村民的选择严重依赖于邻居和媒体宣传。
还受到外场H的影响。与外场方向一致则能量低，更稳定。

总能量：

在这里插入图片描述
用图表示，可以理解为：总能量E = - 边的和x耦合常数 - 节点和x外磁场强度）

节点之间：冲突越少，能量越低；

沿用村民的比喻来说，系统的能量相当于村民观点存在的冲突的数量。如果两个相邻的村民意见不一致，总冲突数就+1，否则就减1。而外场建模了观点的媒体宣传效应,如果村民的观点与舆论宣传一致，则能量越低，因此也越和谐。

蒙特卡罗模拟与玻尔兹曼分布

程序模拟：当前状态 $s_i(t)$ ，和新状态 $s'_i$ 。那么下一次状态 $s_i(t+1)$ 表示为：
$s_i(t+1)=\begin{cases} s'_i \ \ \ with 概率 \mu, \\ s_i(t) \ \ \ with 概率1-\mu. \end{cases}$

其中， $\mu = min\{exp{\frac{E(s_i(t))-E(s'_i)}{kT}} , 1\}$ 即表示状态改变的几率。

如果，下个时间的状态能量比当前大，那么不容易改变；下个时间状态能量比当前小，那么容易改变到这个新状态。可以把 $\mu$ 当作受下一个状态影响的外场，系统倾向于低能量（假设4）。
并且温度T越大，对（假设4）就越否定，使得系统越随机。

这里想到模拟退火的方法。高温下，能量改变几率大；温度下降，打破能量最低原则的概率降低，最终收敛

玻尔兹曼分布：

于是，就进行了一步系统演化。按照上述算法，系统可以最终达到如下的概率分布状态：
$p(\{s_i\}) = \frac{1}{Z}exp(-\frac{E_{\{s_i\}}}{kT}) \\$
其中，配分函数 $Z=\sum_{\{s_i\}}exp(-\frac{E_{\{s_i\}}}{kT})$ , 归一性 $\sum_{\{s_i\}}p(\{s_i\})=1$ ， k 为玻尔兹曼常数，等于1.3806488×10^23

可以从数学上证明，上述随机过程的稳态分布就是根据统计力学计算出来的分布结果。以上方法也被称作：Ising模型的**马尔科夫链-蒙特卡罗(MCMC)**模拟方法，也叫做Metropolis-Hastings算法。

Hopfield神经网络模型

Ising模型的一个显著的性质就是：随着系统的演化，它的能量会自发地降低。我们前面已经提到这种让整体降低能量的方法实际上与拷贝邻居状态的微观原则一致。所以，可以设计一种微观的演化机制，而使得宏观的某种待优化的函数（例如能量）能够自然地被优化。

Hopfield模型通过训练（改变相互连接的权重），可以将要记忆的模式映射为能量最小的状态，之后通过Ising模型的邻域相互作用规则自发演化到这种最小能量状态。

假设每个神经元有两种状态：激活、未激活，用 $s_i=\{+1, -1\}$ 表示。神经元 i 和 j 的连接用权重 $w_{ij}$ 表示。

初始：用向量表示每个神经元激活和未激活的状态。每个时间步，每个神经元更新规则如下：
$s_i(t+1)=\begin{cases} 1 \ \ \ if \sum_{j}w_{ij}s_j(t)>\theta_i, \\ -1 \ \ \ otherwise. \end{cases}$

其中， $\theta$ 为常数阈值。 $\sum_{j}w_{ij}s_j(t)$ 表示与 $s_i$ 连接的所有神经元的加权值，易知这个符合(假设4，最低能量原则)。

能量函数定义为：
$E_{\{s_i\}}=-\sum_{ij}w_{ij}s_is_j - \sum_{i}\theta _is_i$

与Ising模型不同之处： $w_{ij}$ 因连接而异（变连续），外场 $\theta_i$ 因神经元而异（因神经元而异的外场）。

权重学习：
$w_{ij} = \sum^m_{v=1}V_v^iV_v^j$
其中，V表示一组n维神经元，总共有m组， $V^i$ 表示第 i 个分量。

之后，我们就用这组权重作为Hopfield网络中的连接权重，然后针对任意一个输入数据作为神经元的初始状态，按照Hopfield的运行规则演化，系统将逐渐收敛到已记忆过的向量 $V_1,V_2,V_3,...,V_m$ 中的一个。
在这里插入图片描述

2. 受限玻尔兹曼

玻尔兹曼分布（Boltzmann distribution）

基于能量的模型，即分布率是非负的。 $\tilde{p}=\frac{exp(-E(x))}{Z}$ , 配分函数Z、
能量函数: $E(x)=-x^{T}Ux-b^{T}x$ , 权重U、偏置b
自由能 : $F(x)=-log\sum\tilde{p}_{modle}(x)=-log\sum\limits_{h}exp(-E(x,h))$

玻尔兹曼机（Boltzmann Machine）

玻尔兹曼机（Boltzmann Machine）：基于玻尔兹曼能量的模型都称作玻尔兹曼机。

例子：存在可见层、隐层的全链接无向图

受限玻尔兹曼机（RBM）

例子：存在可见层、隐层的全链接无向图，但相同层内无链接
这样使得可见层/隐层，层内单元独立
能量函数，联合概率分布： $P(\bold{v}=\boldsymbol{v},\bold{h}=\boldsymbol{h})=\frac{1}{Z}exp(-E(\boldsymbol{v},\boldsymbol{h})))$

3. Sigmoid

RBM

在这里插入图片描述
² ³

二、从sigmoid函数到指数族分布

1. 对数线性模型

定义几率比：发生与不发生的概率比 $\frac{p}{1-p}$
对数线行模型：几率比取对数后用线行表达 $log\frac{p}{1-p}=\theta^TX$

从对数线性模型容易推得
$log\frac{p}{1-p}=\theta^TX \\ \Rightarrow \frac{p}{1-p}=e^{\theta^TX} \\ \Rightarrow p=\frac{1}{1+e^{-\theta^TX}}$

2. 指数族分布（Exponential family distribution）

⁴
$p(y;\eta)=b(y)exp(\eta^TT(y)-a(\eta))$
其中， $\eta$ 为自然参数 nature parameter ； $T (y)$ 为 充分统计量 sufficient statics ；T(y)一般为y；

当a、b、T都确定时，就确定了一个以 $\eta$ 为参数的指数族分布。

一、选择二项分布（伯努利分布）作为例子来推导：
$p(y;\phi) \\=\phi^y(1-\phi)^{1-y} \\ =exp(ylog(\phi)+(1-y)log(1-\phi)) \\= exp(ylog\frac{\phi}{1-\phi}+log(1-\phi))$
所以，对于伯努利分布来说，
$T(y)=y;\\ b(y)=1; \\\eta=log\frac{\phi}{1-\phi};\\ a(\eta)=-log(1-\phi)=log(1+e^\eta)$

二、选择高斯分布来推导
高斯分布的方差与线性模型的假设函数无关，所以将方差设为1.
$N(\mu,1)\\=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}(y-\mu)^2)\\=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}y^2--\frac{1}{2}\mu^2+y\mu)\\=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}y^2)exp(\mu y -\frac{1}{2}\mu^2)$
所以，
$b(y)=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}y^2)\\ T(y)=y \\ \eta=\mu \\a(\eta)=\frac{1}{2}\mu^2$

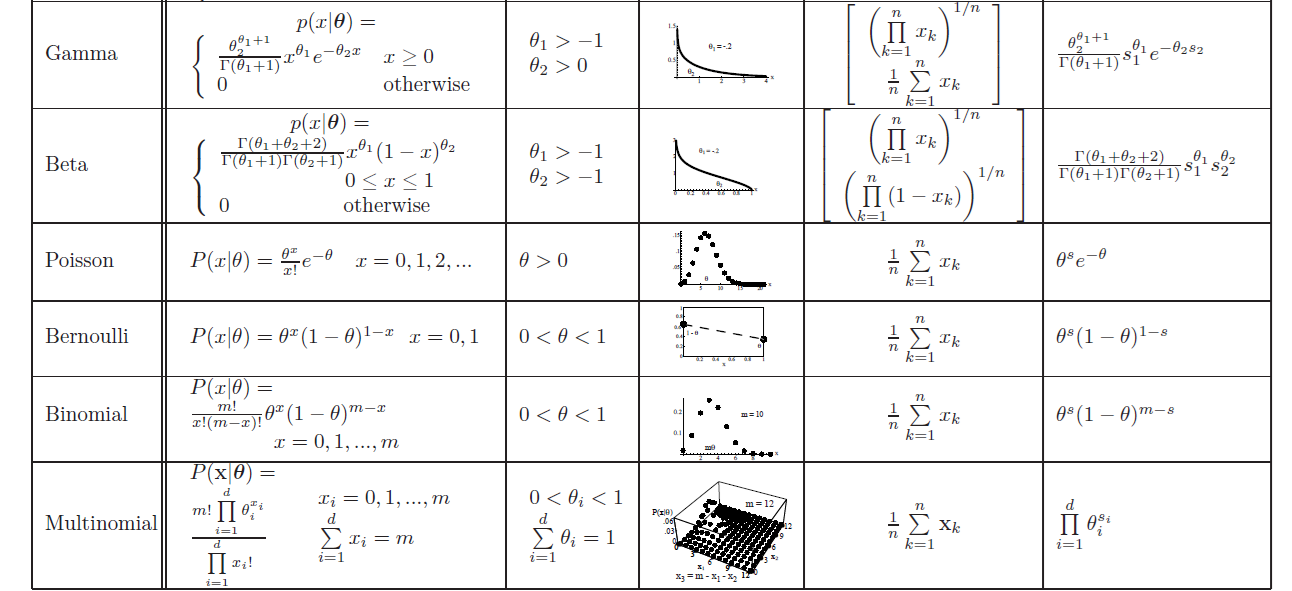
在这里插入图片描述

3. 广义线行模型(Generalized Linear Model，GLM)

对于指数族分布 $p(y;\eta)$ 的自然参数 $\eta$ ，有什么意义呢？
以伯努利分布为例， $\eta=log\frac{\phi}{1-\phi}\Rightarrow \phi=\frac{1}{1+e^{-\eta}}$ ，这里看出其他分布的参数通过不同的函数可以得到 $\eta$ ，反之 $\eta$ 可以通过不同的函数的到其他分布的参数。

GLM三个假设:

$p(y|x;\theta) \sim ExpFamily(\eta)$ ，对于给定的样本x与参数 $\theta$ ，y（样本的分类）服从某个以 $\eta$ 为参数的指数族分布；
给定x，要求x下的充分统计量的期望。目标函数为 $h_\theta(x)=E[T(y)|x]$ ，一般T(y)=y，所以目标一般 $h_\theta(x)=E[y|x]$
$\eta=\theta^Tx$ ，参数 $\eta$ 和输入x是线性相关的

以上假设什么意思？
有一堆数据{x}和y的值域(类的数目)，想要通过一个分布函数 $p (y ∣ x; h)$ 模型对x进行分类，如何做？利用指数族分布学习模型 $p(y;\eta)$ (假设一).

指数族分布是一个抽象的形式 $p(y;\eta)$ ，也有具体的分布，如伯努利分布、正态分布等。显然我们根据y的值域（想分的类）选择了具体的分布 $p (y ∣ x; h)$ 。如何通过通用的方法得到具体分布的参数呢？
假设能够通过 $x$ 线性得到 $\eta$ 。 $\eta=\theta^Tx$ (假设3) 。
再告诉你有一个目标函数 $h_\theta(x)=E[T(y)|x]$ (假设2) ，表示如何对充分统计量 $h$ 进行估计，这样就可以得到统计量的参数 $h$ 了，而且是全部的参数 $h$
震惊！那我还用参数 $h$ 干嘛，直接投入大佬怀抱 ~~p(y|x;h)~~ $p(y|x;\theta)$
重新写一下假设一： $p(y|x;\theta) \sim ExpFamily(\eta)$

GLM例子：

假设样本x服从伯努利分布:
充分统计量 $h_\theta(x)=E[y|x]=p(y=1|x;\theta)=\phi=\frac{1}{1+e^{-\eta}}=\frac{1}{1+e^{-\theta^Tx}}$
所以，利用逻辑回归可以的到伯努利分布的充分统计量(参数)， $\phi=sigmoid(x)$ ，即 $p(y=1|x;\theta)=sigmid(\theta^Tx)$

称这种将自然参数 $\eta$ 与统计量联系起来的函数为正则相应函数（canonical response function），如 $\phi=\frac{1}{1+e^{-\eta}}$

假设样本线性回归模型的 y服从高斯分布:
充分统计量 $h_\theta(x)=E[y|x]=E(N(\mu,\sigma^2))=\mu=\eta=\theta^Tx$
所以， $p(y|x;\theta)=N(\theta^Tx,\sigma^2)$

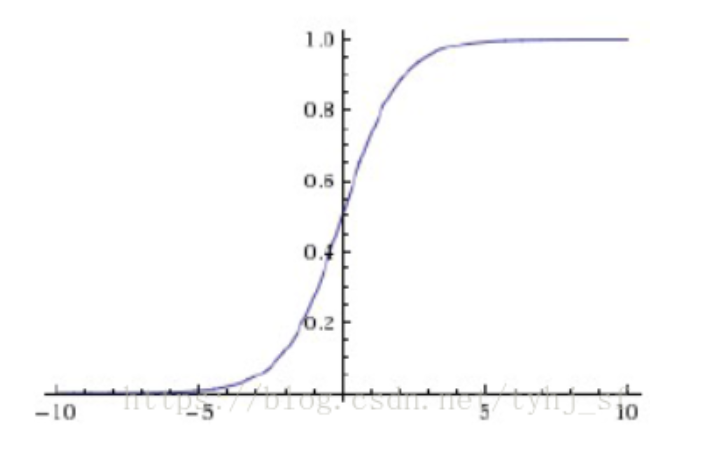
三、Sigmoid 激活函数

sigmoid激活函数

$g(z)=\sigma(z)$

只有z
在这里插入图片描述

双曲正切激活函数

$g (z) = t a n h (z)$
在这里插入图片描述

其中， $tanh(z)=2\sigma(2z)-1$

https://wiki.swarma.org/index.php?title=%E4%BC%8A%E8%BE%9B%E6%A8%A1%E5%9E%8B_Ising_Model ↩︎
https://www.zhihu.com/question/24259872 ↩︎
https://www.zhihu.com/question/22981388/answer/71913037 ↩︎
https://blog.csdn.net/stdcoutzyx/article/details/9207047 ↩︎