傅里叶有限级数

听海边涛声

已于 2024-01-27 15:24:29 修改

阅读量381

点赞数 1

文章标签：数学

于 2024-01-27 14:29:38 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/panghuangang/article/details/135882511

版权

文章探讨了傅里叶级数在表示周期函数时，如何通过有限项级数进行近似，介绍了均方误差的概念以及随着项数增加会出现的吉布斯现象，通过实例展示了矩形波和锯齿波的吉布斯效应。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

傅里叶有限级数

一般来说，任意周期函数表示为傅里叶级数时，需要无限多项才能完全逼近原函数。但在实际应用中，不可能取无限多项，而是取有限项级数来代替无限项级数。

已知周期函数 $f(t)$ 的傅里叶级数为

$f(t)=a_{0}+\sum_{n=1}^{\infty }(a_{n}\cos n\omega t+b_{n}\sin n\omega t)$

若取傅里叶级数的前 $2N+1$ 项来逼近 $f(t)$ ，则有限项傅里叶级数为

$S_{N}(t)=a_{0}+\sum_{n=1}^{N }(a_{n}\cos n\omega t+b_{n}\sin n\omega t)$

均方误差

这样用有限项来逼近的误差为

$\varepsilon _{N}(t)=f(t)-S_{N}(t)$

均方误差等于

$E_{N}=\overline{\varepsilon _{N}^{2}(t)}=\frac{1}{T}\int_{-T/2}^{T/2}\varepsilon _{N}^{2}(t)dt$

将 $f(t)$ 和 $S_{N}(t)$ 代入，并经过化简，得到

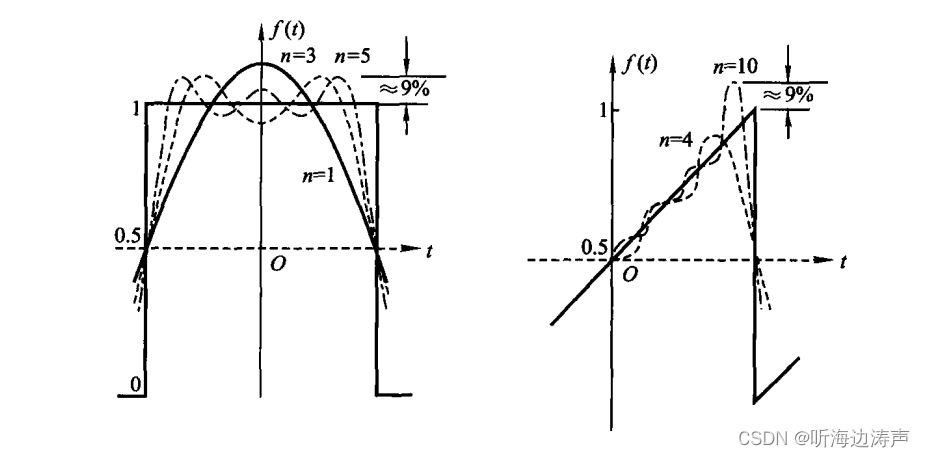
$E_{N}=\overline{\varepsilon _{N}^{2}(t)}=\overline{f^{2}(t)}-\left [ a_{0}^{2} +\frac{1}{2}\sum_{n=1}^{N}(a_{n}^{2}+b_{n}^{2})\right ]$

吉布斯（Gibbs）现象

当选取傅里叶有限级数的项数越多，在所合成的波形 $S_{N}$ 中出现的峰起越靠近 $f(t)$ 的不连续点。当所选取的项数 $N$ 很大时，该峰起值趋向于一个常数，大约等于总跳变值的9%，并从不连续点开始以起伏震荡的形式逐渐衰减下去。这种现象称为吉布斯（Gibbs）现象。

下面矩形波和锯齿波所呈现的吉布斯现象的图来自《信号与系统_第三版_郑君里_上》：

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。