关注作者了解更多
我的其他CSDN专栏
关注作者了解更多
资料来源于网络，如有侵权请联系编者
目录
微分方程是时域中的数学模型，传递函数是采用L[ ]法求解微分方程时引申出来的复频域中的数学模型，它不仅可以表征系统的动态性能，而且可以用来研究系统的结构和参数变化时对系统性能的影响，是经典控制理论中最重要的模型。
1 定义 在线性定常系统中，当初始条件为零时，系统输出拉氏变换与输入拉氏变换的比，称为传递函数，用G(S)表示。
可见，输入与输出之间的关系仅取决于电路的结构形式及其参数（固有特性）,与输入的具体形式无关，无论输入如何，系统都以相同的传递作用输出信息或能量，因此称之为传递函数。 传递函数是代数式，其传递作用还经常用方框图直观的表示：
一般的，设线性定常系统的微分方程式如下，
r为输入量，c为输出量，对两式进行拉式变换得到传递函数
G(s)是由微分方程经线性拉氏变换得到，故等价，只是把时域变换到复频域而已，但它是一个函数，便于计算和采用方框图表示，广泛应用。
其分母多项式就是微分方程的特征多项式，决定系统的动态性能。从描述系统的完整性来说，它只能反应零状态响应部分。但在工程实际当中：
1）都是零初始条件的，即系统在输入作用前是相对静止的，即输出量及其各阶导数在t =0的值为零。
2）输入在t =0以后才作用于系统，即输入及其各阶导数在t =0的值为零； 对于非0初始条件时，可采用叠加原理。
2.4.3 传递函数的性质
(a)传递函数是一种数学模型，与系统的微分方程相对应。
(b)传递函数是系统本身的一种属性，与输入量的大小和性质无关。
(c)传递函数只适用于线性定常系统，因为拉氏变换是一种线性变换。
(d)传递函数描述的是一对确定的变量之间的传递关系，对中间变量不反应。
(e)传递函数是在零初始条件下定义的，因而它不能反映在非零初始条件下系统的运动情况。（零状态解）
(f)传递函数一般为复变量s 的有理分式，它的分母多项式是系统的特征多项式，且阶次总是大于或等于分子多项式的阶次，即n > m。并且所有的系数均为实数。
(g)传递函数与脉冲响应一一对应，是拉氏变换与反变换的关系。
（2）G(s)的微观结构
G(s)是关于s的有理分式，可分解成多种形式：
1）零极点表达式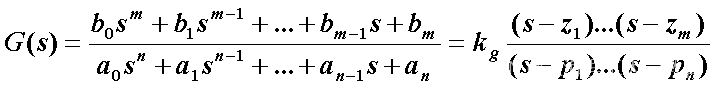
其中，kg为根轨迹增益
可知：传递函数定，零、极点和kg唯一确定，反之亦然。因此传递函数可用零极点和传递系数等价表示。
零极点既可以是实数，也可以是复数，表示在复平面上，形成的图称传递函数的零、极点分布图。反映系统的动态性能。因此对系统的研究，可变成对系统传函的零、极点的研究了，这就是根轨迹法(chaper4)。
例如，试画出下面传递函数的零极点图。
2）时间常数表达式
较容易分解成一些典型环节，chapter5 应用
2-6 典型环节及其传递函数
自动控制系统可以用传递函数来描述，任一复杂的传递函数G(s)，都可表示为：
可看成是若干称为典型环节的基本因子的乘积，一般认为典型环节有6种，这些典型环节,对应典型电路。这样划分对系统分析和研究带来很大的方便。 分述如下：
1.比 例环节
（杠杆，齿轮系，电位器，变压器等）
运动方程式 c(t) = K r(t)
传递函数 G(s) = K
单位阶跃响应 C(s) = G(s) R(s) = K/s
c(t) = K1(t)
可见，当输入量r(t)=1(t)时，
输出量c(t)成比例变化。
2.惯性环节
由微分方程式可以得到传递函数
3.积分环节
当输入阶跃函数时，该环节的输出随时间直线增长，增长速度由1/T决定。当输入突然除去，积分停止，输出维持不变，故有记忆功能。
4.微分环节
由于阶跃信号在时刻t = 0有一跃变，其他时刻均不变化，所以微分环节对阶跃输入的响应只在t = 0时刻产生一个响应脉冲。
5.二阶振荡环节
由微分方程式得到传递函数，振荡环节有一对位于s左半平面的共轭极点。
得到二阶振荡环节的阶跃响应曲线，分析动态性能。
6、延迟环节
他的微分方程式，传递函数，单位阶跃响应如上
关注作者了解更多
我的其他CSDN专栏
关注作者了解更多
资料来源于网络，如有侵权请联系编者
扫一扫
5004
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
