【数字信号处理】第二章 z变换，z变换的收敛域，逆z变换

---

关注作者了解更多

我的其他CSDN专栏

过程控制系统

工程测试技术

虚拟仪器技术

可编程控制器

工业现场总线

数字图像处理

智能控制

传感器技术

嵌入式系统

复变函数与积分变换

单片机原理

线性代数

大学物理

热工与工程流体力学

数字信号处理

光电融合集成电路技术

电路原理

模拟电子技术

高等数学

概率论与数理统计

数据结构

C语言

模式识别原理

自动控制原理

数字电子技术

关注作者了解更多

资料来源于网络，如有侵权请联系编者

目录

2.1引言

2.2 z变换的定义与收敛域

一。z变换的定义  

二，z变换的收敛域

1.有限长序列

2.右边序列

3.左边序列

4.双边序列

3.2.2 Z变换收敛域的特性

3.2.4 逆z变换

---

2.1引言

         信号与系统的分析方法除时域分析方法外，还有变换域分析方法。在连续时间信号与系统中，其变换域方法就是拉普拉斯变换与傅里叶变换。在离散时间信号与系统中，变换域分析方法是z变换法和傅里叶变换法。z变换在离散时间系统中的作用就如同拉普拉斯变换在连续时间系统中的作用一样，他把描述离散系统的差分方程转换位简单的代数方程，使其求解大大简化。因此，对求解离散时间系统而言，z变换是一个极重要的数学工具。

2.2 z变换的定义与收敛域

一。z变换的定义  

若序列为x（n），则幂级数

称为序列x（n）的z变换，其中z为变量。亦可将x（n）的z变换表示为

二，z变换的收敛域

   显然，只有当（2-1）式的幂级数收敛时，z变换才有意义。

  对任意给定序列x（n），使其z变换收敛的所有z值的集合称为X（z）的收敛域。

按照级数理论，（2-1）式的级数收敛的必要且充分条件是满足绝对可和的条件，即要求

要满足此不等式，z值必须在一定的范围内才行，这个范围就是收敛域，不同形式的序列其收敛域形式不同。分别讨论如下。

1.有限长序列

  这类序列是指在有限区间n1<n<n2  之内序列才具有非零的有限值，在此区间外，序列值皆为零，其z变换为

 因此，X（z）是有限项级数之和，故只要级数的每一项有界，则级数就收敛，及要求

显然，在0<z<正无穷上，都满足此条件，也就是说收敛域至少是除z=0或z=正无穷之外的开界。

2.右边序列

    这类序列是指只在n>n1时，x（n）有值，在n<n1时，x（n）=0，其z变换为

  此式右端第一项为有限长序列的z变换，按照上面讨论可知，它的收敛域为有限z平面，而第二项时z的负幂级数，按照级数收敛的阿贝尔定理可推知，存在一个收敛半径R，级数在以原点为中心，以R为半径的圆外任何点都绝对收敛。因此综合此二项，只有二项都收敛时级数才收敛。所以，如果R是收敛域的最小的半径，则右边序列z变换收敛域为

  右边序列及其收敛域如图2-2所示

  因果序列是最重要的一种右边序列，即n1=0的右边序列，也就是说，在n>0时，x（n）有值，n<0时，x（n）=0.

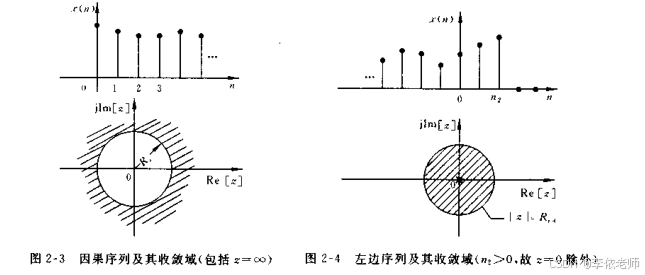
3.左边序列

这类序列指只在n<n2时，x（n）有值，n>n2时，x（n）=0，其z变换为

 等式第二项是有限长序列的z变换，收敛域为有限z平面，第一项是正幂级数，按阿贝尔定理，必存在收敛半径R,级数在以原点为中心，以R为半径的圆内任何点都绝对收敛。如果R为收敛域的最大的半径，则综合以上两项，左边序列z变换的收敛域为

4.双边序列

    这类序列是指n为任意值时（正、负、零）x（n）皆有值的序列，可以把它看成一个右边序列和一个左边序列之和，即

   

  因而其收敛域应该是右边序列与左边序列收敛域的重叠部分，等式右边第一项为右边序列，其收敛域

3.2.2 Z变换收敛域的特性

   例3.25 

  当0<a<1时，x（n）的波形既X(Z)的收敛域如下图所示

常见序列的Z变换及收敛域

3.2.4 逆z变换

    已知序列的z变换及其收敛域，求序列称为逆Z变换。序列的Z   变换及其逆z变换表示如下

  式中，c时收敛域内一条逆时针的封闭曲线

1.幂级数法

  按照Z变换的定义，可用长除法将X(Z)写成幂级数形式，技术的系数就是序列x(n)

如果x(n)是右序列，级数应是负幂级数，分子分母应按z的降幂排列

如果x(n)是左序列，级数则是正幂级数，分子分母应按z的升幂排列

常见序列的Z变换及其收敛域

例题