8.1 向量及其线性运算

本篇开始进行向量代数和空间解析几何的内容的总结。

一、定义

1. 向量：既有大小又有方向的量称为向量，又叫矢量。
   向量由大小（长度）和方向唯一确定的，与起点和位置无关，这样的向量称为自由向量。

2. 向量相等：向量相等有两个条件，大小（长度）相等，方向相同。

3. 向量的模
   

4. 向量的夹角

二、向量的线性运算

1. 向量加法
   ①平行四边形法则
   
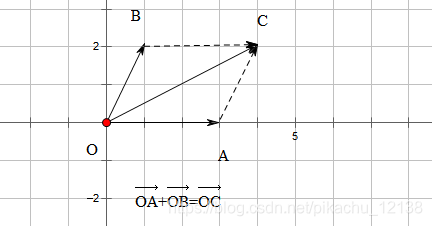
   如图，两个向量相加，做两个向量的平行向量组成平行四边形，即可得到结果向量

②三角形法则

从向量OA起点指向向量AB终点的向量即为两个向量之和

向量加法的符合加法交换律，这里就不说了，中学知识。

2. 向量减法
   
   从减向量终点指向被减向量终点的向量即为二者之差

3. 数与向量的乘法
   

三、空间直角坐标系

第Ⅰ卦限：x>0;y>0;z>0
第Ⅱ卦限：x<0;y>0;z>0
第Ⅲ卦限：x<0;y<0;z>0
第Ⅳ卦限：x>0;y<0;z>0
第Ⅴ卦限：x>0;y>0;z<0
第Ⅵ卦限：x<0;y>0;z<0
第Ⅶ卦限：x<0;y<0;z<0
第Ⅷ卦限：x>0;y<0;z<

四、向量线性运算的代数描述

五、向量的模、方向角与方向余弦、投影

• 向量的模，即为向量的长度
  参考上图可得，向量的模为分量的平方和开根号。
  两点之间的距离，实际上也就是两点所成向量的模长。
  
• 方向角与方向余弦
  

---

a向量与x、y、z轴的正方向的夹角称为向量a的方向角，记作α、β、γ
称cos α、cos β、cos γ 为a向量的方向余弦

例1

---

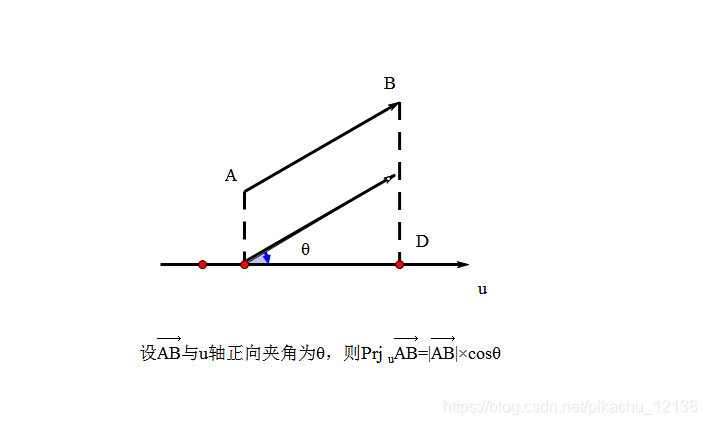
本篇完。