量子傅里叶变换电路实现
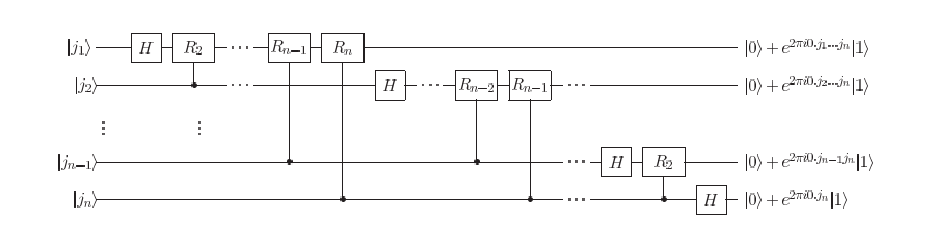
注意这里的 R k R_k Rk门是单比特门
R = [ 1 0 0 e 2 π i / 2 k ] R = \begin{bmatrix} 1&0\\ 0&e^{2\pi i/2^k} \end{bmatrix} R=[100e2πi/2k]
我们注意到一个量子 ∣ j 1 j 2 . . . j n ⟩ |j_1j_2...j_n\rangle ∣j1j2...jn⟩经过量子傅里叶变换后变为
∣ j 1 j 2 . . . j n ⟩ ⟶ Q F T ( ∣ 0 ⟩ + e 2 π i 0. j n ∣ 1 ⟩ ) ( ∣ 0 ⟩ + e 2 π i 0. j n − 1 j n ∣ 1 ⟩ ) . . . ( ∣ 0 ⟩ + e 2 π i 0. j 1 j 2 . . . j n ∣ 1 ⟩ ) 2 n / 2 |j_1j_2...j_n\rang\stackrel{QFT}{\longrightarrow}\frac{(|0\rang+e^{2\pi i0.j_n}|1\rang)(|0\rang+e^{2\pi i0.j_{n-1}j_n{}}|1\rang)...(|0\rang+e^{2\pi i0.j_1j_2...j_n}|1\rang)}{2^{n/2}} ∣j1j2...jn⟩⟶QFT2n/2(∣0⟩+e2πi0.jn∣1⟩)(∣0⟩+e2πi0.jn−1jn∣1⟩)...(∣0⟩+e2πi0.j1j2...j








 本文详细介绍了量子傅里叶变换电路的实现过程,通过分析Rk门和H门的作用,逐步展示量子比特如何通过一系列操作转化为量子傅里叶变换后的状态。量子计算机在执行离散傅里叶变换时,相较于传统计算机展现出指数级的加速优势。
本文详细介绍了量子傅里叶变换电路的实现过程,通过分析Rk门和H门的作用,逐步展示量子比特如何通过一系列操作转化为量子傅里叶变换后的状态。量子计算机在执行离散傅里叶变换时,相较于传统计算机展现出指数级的加速优势。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 9585
9585

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








