关于WGAN的学习总结——Lipschitz约束与正则化

写在前面的话

真是觉得数学决定了人工智能的上限，不得不佩服数学专业的大佬，WGAN还是比较经典的GAN网络，其结果也蛮好的（跑的MNIST数据集），但是损失看了代码也没看懂咋算的，所以还是得从数学原理上详细推导一下，然而很多博客一知半解，有幸看到介绍很完善的推导，尝试记录一些学习理解到的内容，能力有限，如有理解错误还请指出，不胜感激。

1. 范数

L-P范数，p可以为任意自然数

$$L_p=||x|{|}_p=\sqrt[p]{\sum _{i=1}^n{x}_i^p},x=(x_1,x_2,\dots ,x_n)$$

简单来说，0范数就是非0元素的个数，1范数就是各个元素绝对值之和……

2. 泛化

在深度学习中，总是提到网络的泛化能力，其实就是指模型对输入扰动是不敏感的。如图像二分类来说，只改变一个像素值就分成不同的类别，这就说明模型过拟合，对输入过于敏感。

稳定性包含两种含义：

• 参数扰动的稳定性
  $$f_{w+\Delta w}(x)\approx f_w(x)$$
• 输入扰动的稳定性
  $$f_w(x+\Delta x)\approx f_w(x)$$

对于神经网络模型，都是希望对输入的变动不敏感，即希望 $||x_1-x_2||$ 很小时，$||f_w(x_1)-f_w(x_2)||$ 也尽可能地小

2.1. Lipschitz约束与L约束

我理解的两者其实表示同一种约束或是包含关系，之所以分开表述是因为还是有细微的差别

1. Lipschitz 约束，式中左侧采用的是函数值差异，也可以是各阶梯度值的差异，右侧的 $L$ 是常数

$$||f_w(x_1)-f_w(x_2)||\le L\cdot |x_1-x_2||$$

如下图是用在函数值上的约束，是为了不让函数值变化的太快，将函数约束在粉色区域内

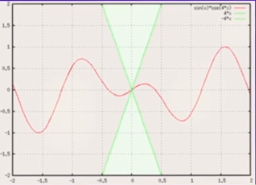
如果梯度是L-Lipschitz的，拿二次来说，就有了一个二次函数的上界
$$f(x)\le f(x_0)+<\nabla f(x_0),x-x_0>+\frac{L}{2}||x-x_0|{|}^2,\forall x$$

如果函数是严格凸函数，那么就有了一个二次函数的下界
$$<\nabla f(x_0),x-x_0>+\frac{\mu }{2}||x-x_0|{|}^2\le f(x),\forall x$$

这样就可以将目标函数约束到一个二次函数的范围内，同理，这个二次函数可以推广到更高次的函数

2. L 约束

$$||f_w(x_1)-f_w(x_2)||\le C(w)\cdot |x_1-x_2||$$

$C(w)$ 只与参数有关，与输入无关，希望 $C(w)$ 越小越好，越小意味着它对输入扰动越不敏感，泛化性越好

考虑单层的全连接 $f(Wx+b)$，让 $x1,x2$ 充分接近，那么就可以将左边用一阶项近似得到（假设两式相减后b消掉了）
$$\frac{\partial f}{\partial x}W(x_1-x_2)\le C(w,b)\cdot ||x_1-x_2||$$

$\frac{\partial f}{\partial x}$ 这一项（每个元素）的绝对值必须不超过某个常数，这就要求我们要使用“导数有上下界”的激活函数，不过我们目前常用的激活函数，比如sigmoid、tanh、relu等，都满足这个条件。神经网络均可以看作是全连接的结果，因此问题可以转换为
$$||W(x_1-x_2)||\le C||x_1-x_2||(1)$$

为使上式恒成立，那么要尽可能使 $C$ 小，从而给参数带来一个正则化项 $C^2$

这时候需要引入一个新的范数，Frobenius范数，简称F范数
$$||W|{|}_F=\sqrt[]{\sum _{i,j}{w}_{ij}^2}$$

由柯西不等式可证明（不是数学专业，早忘柯西了）
$$||Wx||\le ||W|{|}_F\cdot ||x||$$

因此，如果不大关心精准度，直接可以取 $C=\Vert W{\Vert }_F$

2.2 正则项

在原博客中 $\Vert W{\Vert }_2$ 是式(1)中最准确的 $C$（所有满足式(1)的 $C$ 中最小的那个），我不理解，但是我又证不出来

为了使神经网络尽可能好地满足L约束，我们应当希望 $ C=∥W∥_2$ 尽可能小，我们可以把C2作为一个正则项加入到损失函数中。还没有算出谱范数 $\Vert W{\Vert }_2$ ，但算出了一个更大的上界 $\Vert W{\Vert }_F$ ，所以我们可以得到新的loss
$$loss=loss(y,f_w(x))+\lambda \Vert W{\Vert }_F^2$$

带入表达式可以得到实际上就是 l2正则化，表明L2正则化能使得模型更好地满足L约束，从而降低模型对输入扰动的敏感性，增强模型的泛化性能。

3. 思考

才看了关于WGAN优化的详细推导，其中涉及到 1-Lipschitz 连续问题，这也是之前一直疑惑的地方，因此对于其详细原理又进行了学习。关于Lipschitz连续的问题，前提是明白Lipschitz条件是用来做什么，我用一句话概括就是通过该条件为最优化问题提供一个上界的约束，从而使函数优化更高效且更稳定，当满足Lipschitz连续后则使整个网络得到稳定的训练，因此GAN网络中更加需要这样的条件吧。

在之前的博客中提到的SAGAN中提到了谱归一化，当时仅明白其计算，但是详细实现我还未看源码，我也需要跑一下其代码好好理解一下用法和思想。

4. 参考链接

[1] 苏剑林. (2018, Oct 07). 《深度学习中的Lipschitz约束：泛化与生成模型 》[Blog post].
[2] 非凸优化基石：Lipschitz Condition
[3] 论文就不放了