Minimum Snap轨迹规划详解（2）corridor与时间分配

在上一篇文章中，我们得到的轨迹并不是很好，与路径差别有点大，我们期望规划出的轨迹跟路径大致重合，而且不希望有打结的现象，而且希望轨迹中的速度和加速度不超过最大限幅值。为了解决这些问题有两种思路：

• 思路一：把这些”期望“加入到优化问题中。
• 思路二：调整时间分配，来避免这些问题。

1.corridor

1.1 corridor是什么？

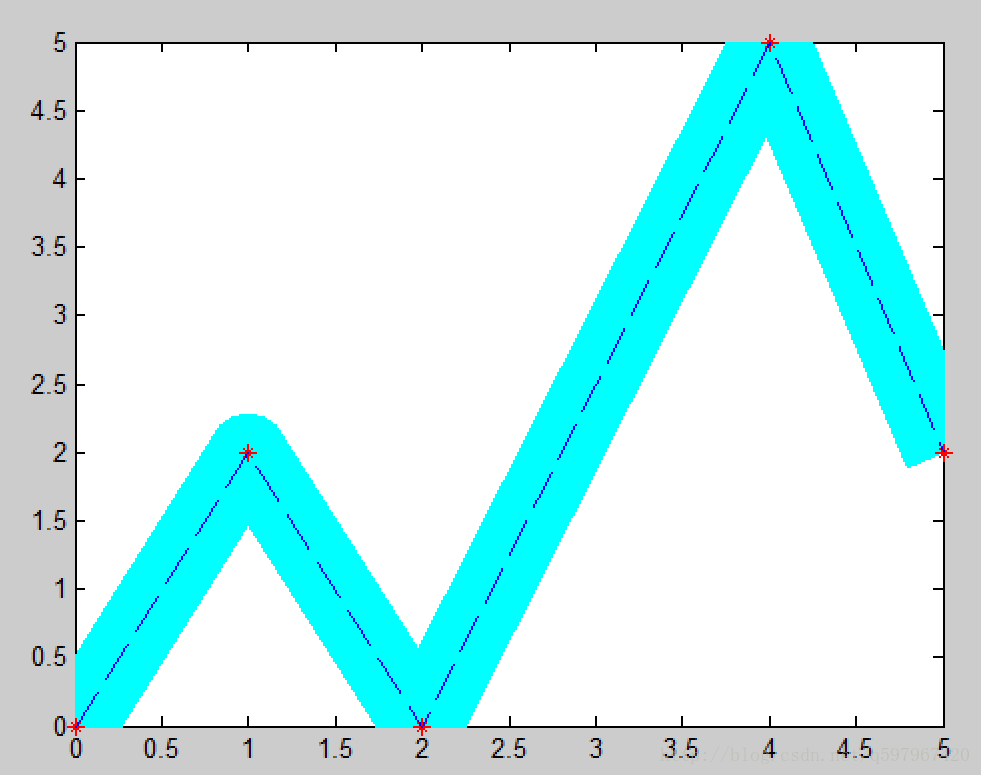
为了限制轨迹的形状，引入了corridor的概念，corridor可以理解为可行通道，如下图，规划出的轨迹必须在corridor内。直观的思路是：如果能把corridor当作约束加入到QP问题中，那么解得的轨迹自然就在corridor内了。

1.2 corridor约束怎么加？

很容易想到，把之前的等式约束$Ap=d$改成不等式约束$Ap\leq d_1$和$Ap\geq d_2$。然而，不管是等式约束还是不等式约束，都是针对一个特定的时刻，而实际希望的是对所有时刻$t \in [0,T]$，都需要在corridor中。
一个简单粗暴的思路：在路径上多采样一些中间点，每个中间点都加corridor约束。尽管这种方法理论上只能保证采样点在corridor中，但实际过程中，如果corridor大小和采样步长设置得合理，而且不Fix waypoints，能work的比较好。这里不fix 中间点的位置，是为了去掉中间点的强约束，尽量避免轨迹打结，实际中，我们也是不一样要求轨迹完全经过中间点，只要在那附近（corridor）内就行。

1.3 构造corridor不等式约束

为了方便构造，对于每一个采样点$pt$，我们施加一个矩形的corridor，即

$$x_{min}\leq pt_x \leq x_{max},~y_{min}\leq pt_y \leq y_{max}$$
这里用矩形corridor是因为斜线corridor（平行四边形）不好构造，而且我们只需要大致在corridor里面就好，没有必要非弄一个严格的斜线corridor。对于每个采样点，设矩形corridor的边长为 $2r$，增加两个位置不等式约束：

[1,ti,t2i,...,tni]p≤p(ti)+r[−1,−ti,−t2i,...,−t