YOLO系列基础（四）从归一化层（BN层）到CBS模块

千天夜

已于 2024-12-04 18:13:37 修改

阅读量1.6k

点赞数 18

分类专栏： YOLO模型相关知识积累机器学习文章标签： YOLO 卷积神经网络学习人工智能 python 计算机视觉 cnn

于 2024-11-12 10:36:45 首次发布

内容如果有帮到你，求求给个点赞关注思密达~

本文链接：https://blog.csdn.net/qiantianye/article/details/143689977

版权

知识积累同时被 3 个专栏收录

54 篇文章

订阅专栏

YOLO模型相关

33 篇文章

订阅专栏

机器学习

20 篇文章

订阅专栏

to 公司数据合规同事，本文为在家编写博客后采用定时发送机制发送的博文，没有用到任何公司信息和公司代码

系列文章地址

YOLO系列基础合集——小白也看得懂的论文精解-CSDN博客

YOLO系列基础（一）卷积神经网络原理详解与基础层级结构说明-CSDN博客

YOLO系列基础（二）Bottleneck瓶颈层原理详解-CSDN博客

YOLO系列基础（三）从ResNet残差网络到C3层-CSDN博客

YOLO系列基础（四）归一化层（BN层）的前世今生！-CSDN博客

YOLO系列基础（五）从神经元共适应性到模型Dropout层-CSDN博客

YOLO系列基础（六）YOLOv1原理详解原理如此清晰-CSDN博客

YOLO系列基础（七）从数据增强到图像线性变换-CSDN博客

YOLO系列基础（八）从坐标直接预测到锚框偏移量-CSDN博客

YOLO系列基础（九）YOLOv2论文及原理详解（上）-CSDN博客

YOLO系列基础（十）YOLOv2论文及原理详解（下）Darknet-19网络结构-CSDN博客

系列文章地址

背景

归一化层的前世今生

神奇的内部协变量位移（Internal Covariate Shift）

归一化层（Batch Normalization层）

BatchSize简介（在BN层计算操作之前）

背景

随着YOLOv11版本的发布，YOLO算法在视觉检测领域独领风骚，本系列旨在从小白出发，给大家讲解清楚视觉检测算法的前世今生，并讲清楚YOLOv11版本算法的所有模块功能！

在此之前，需要大家了解之前系列文章的内容，前两篇主要讲解卷积池化全连接三大基础层、瓶颈层、C3层的主要内容。若看客已经清楚相关内容，可以直接往下看，若不清楚，则可以去相应的链接了解了解哦~

归一化层的前世今生

神奇的内部协变量位移（Internal Covariate Shift）

内部协变量位移是指在深度神经网络训练过程中，由于每一层的输入分布随着网络参数的更新而发生变化，导致网络层与层之间的输入分布不一致的现象。这种位移主要来源于两个方面：

网络参数更新：在训练深度神经网络时，每一层的参数（如权重和偏置）都会随着训练的进行而不断更新。这种更新一来导致前一层的输出分布发生变化，二来又影响到后一层的输入分布。
数据层内操作：每一层的输入数据经过层内操作（如卷积、激活函数等）后，其分布也会发生变化。这种变化是逐层累积的，导致高层输入分布的变化非常剧烈。

这会导致什么问题呢？

这会导致深度神经网络在某种程度上失去了训练成功的可能性！

有这么严重？就是有如此严重！我们知道神经网络训练依靠的是反向传播与参数的更新。但是！我们需要注意的是，反向传播，意味着是从后往前更新参数，然而实际上后一层更新参数的一个前提是前一层的分布不发生变化！假设有一层刚刚跟新完，这一层的前端输入就变化了，我的更新岂不是成了笑话？

由于每一层的输入分布都在不断变化，网络需要不断适应这种变化，从而导致训练过程变得异常困难，尤其表现在深度网络中，这种现象尤为明显。

归一化层（Batch Normalization层）

BN层的主要目的是减少内部协变量位移的影响，加速神经网络的训练过程，并提高模型的泛化能力。是由Sergey Ioffe（或Ian Goodfellow，存在不同说法，但Sergey Ioffe是更为广泛认知的提出者之一）和Christian Szegedy等人在2015年的论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》中被提出。

有关于机器学习中的归一化、去中心化、标准化的内容可以参考如下博文：

机器学习（归一化、去中心化、标准化）_数据去中心化-CSDN博客

这是博主之前的博文，在一定程度上解答了部分归一化的作用，本文我们继续深入

注意：归一化层不是对前面层的参数的归一化，而是对前面层输出的数据的归一化，归一化的是特征图的数据，而不是w和b！归一化层并非一个固定不变的操作，依然需要参与训练！

我知道第一次听说这个BN层的看到这会产生疑惑，因为上诉内容都是一个固定的操作，怎么归一化层还需要参与训练呢？别着急，我们慢慢来

还是需要祭出下面这张图，对我们的理解很有帮助

首先我们复习，针对一个3个通道的输入特征图，假设我们需要输出4通道的特征图，我们需要4个过滤器，每个过滤器有3个卷积核。

那么我们BN层在上面的什么位置插入呢？答案是在生成4个特征图之后，在获取最终4通道特征图之前，BN层需要对每一个通道的输出数据进行归一化操作！

        我们为什么是在每一个通道进行BN层操作？为什么不在输出4通道特征图之后进行一次统一的全通道的BN呢？貌似也能达成目标不是吗？

        实际上，这和通道意义有关，在一开始，三通道仅仅指的是rgb三色，但是随着通道数增加 or 减少，通道数实际上意味着不同维度的特征信息。

        我们需要注意的是不同的通道我们选择的卷积核是不一样的，这就导致了输出的特征内容是完全不相干的，我们若是在后面针对全通道进行归一化处理，那么就会一定程度上丢失这些差异性。用机器学习的思路解释就是：类内归一化才是有意义的，不同类之间归一化毫无意义！

BatchSize简介（在BN层计算操作之前）

在我们实际讲解BN层操作之前，我们需要对BatchSize进行一个说明，BatchSize就是模型在单次训练的时候同时训练的图片数量，batchsize = 2 意味着单次训练2张图片，就这么简单。

BacthSize主要是为了加速模型拟合、减少模型过拟合、缓解loss跳变引入的。并非本文重点，我们下篇再详解此部分。

BN层是如何计算的

我感觉第一次接触BN层，到此肯定头晕晕，不要紧，博主尽量言简意赅易于理解~

普通归一化的具体操作为：

计算样本均值。
计算样本方差。
样本数据标准化处理。

公式如下：

$eq?x%5E%7Bi%7D%3D%5Cfrac%7Bx%5E%7Bi%7D-%5Cmu%20%7D%7B%5Cdelta%20%7D$

神经网络的BN层有些许的不同，但是首先我们需要先确定以下内容

每一个通道都需要单独归一化操作
均值和方差是BatchSize内的所有图片再这一个通道上数据的统计值

BN层中均值和方差的计算示例

假设一个batch中有N个样本，每个样本的特征图大小为HxWxC（高度、宽度和通道数）

那么在计算某个通道c的均值时，是将该通道在所有N个样本、H行和W列上的像素值加起来，然后除以N×H×W，得到该通道的均值。
同样地，在计算方差时，也是先计算该通道在所有N个样本、H行和W列上的像素值与均值的差的平方和，然后除以N×H×W，得到该通道的方差。

到此为止，我们已经知晓了BN层80%的疑难内容了，剩下的问题只有一个，BN层是如何参与训练的？因为上面的步骤都是固定的，根本没有参数可以用来更新。欸，这就引出了 $eq?%5Cgamma$ 和 $eq?%5Cbeta$

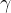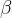
BN层中参与训练的值： $eq?%5Cgamma$ 和 $eq?%5Cbeta$

实际上BN层真正的公式是下面这个：

$eq?x%5E%7Bi%7D%3D%5Cfrac%7Bx%5E%7Bi%7D-%5Cmu%20%7D%7B%5Cdelta%7D%5Ctimes%20%5Cgamma%20+%20%5Cbeta$

数学功底好的看客可能一言看出了问题：我们做了一个标准化的反操作？也就是说我们好不容易将数据转换到均值为0、方差为1的标准正态分布，结果我们自己乘了缩放因子和偏移量？？why？

上诉的归一化处理虽然能够加速训练、提高稳定性，但也在一定程度上限制了模型的表达能力。因为归一化将数据强制转换到均值为0、方差为1的标准正态分布，这会破坏原始数据中的特征分布。

归一化处理破坏原始数据的特征分布，而γ和β能够恢复这种分布。当γ等于原始数据的标准差、β等于原始数据的均值时，线性变换后的数据将恢复到原始分布。

看似很矛盾对不对？实际上这是权力的下放，BN层叫BN层其实并不准确，BN层最准确的说法应当是数据分布处理层。我们需要针对数据分布进行处理，但是又不知道如何才是最好的处理方式？无论是哪种分布都不能完全适配所有的层，所以我们直接把这种权力下放给模型自己，让模型自己去决定最好的数据分布方式吧！

从BN层到CBS层

经过漫长的学习操作，我们熟知了BN层相关原理和操作步骤，我们在此再次强调一下!

特征图输入先给到卷积层进行卷积操作，获取不同通道的特征图
各个通道进入BN层执行对应的BN操作
BN操作后给到激活函数进行激活

一个基本的代码如下：

import torch
import torch.nn as nn
import torch.nn.functional as F

# 定义一个包含卷积层、批量归一化层和SiLU激活层的模块
class CBS(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size=3, stride=1, padding=1):
        super(CBS, self).__init__()
        # 卷积层
        self.conv = nn.Conv2d(in_channels=in_channels, out_channels=out_channels, 
                              kernel_size=kernel_size, stride=stride, padding=padding)
        # 批量归一化层
        self.bn = nn.BatchNorm2d(num_features=out_channels)
        # SiLU激活层（虽然PyTorch没有直接的SiLU层，但可以使用F.silu或nn.SiLU）
        self.silu = nn.SiLU()  # 或者使用 F.silu 在 forward 方法中

    def forward(self, x):
        # 卷积操作
        x = self.conv(x)
        # 批量归一化
        x = self.bn(x)
        # SiLU激活
        x = self.silu(x)
        return x

# 创建一个输入张量，模拟一个批次的大小为1，特征图大小为640x480x3的图像
input_tensor = torch.randn(1, 3, 640, 480)  # 批次大小, 通道数, 高度, 宽度

# 创建CBS网络实例，指定输入和输出通道数
cbs_network = CBS(in_channels=3, out_channels=16)

# 前向传播
output_tensor = cbs_network(input_tensor)

# 打印输出张量的形状
print(output_tensor.shape)  # 预期输出：torch.Size([1, 16, 640, 480])

恭喜你，已经完成CBS模块的学习与操作了。

是的没错，CBS就是卷积（Conv）+ 归一化（BN） + 激活函数（SiLU）！