看图就懂：线性代数之特征值分解与奇异值分解

目录

基向量：

基向量表达：

 变换

 相似矩阵

行列式

特征向量

特征向量作为基向量 

特征基用途

矩阵对角化

特征值分解矩阵

奇异值分解矩阵(SVD) 

奇异值分解性质

基向量：

        基向量是过原点的单位向量，选择一对/组基向量(线性无关)组成参考坐标系，等距平行分布。如下所示

                         

                          U[i，j]                                                                 V[i，j]]   

                 

                          W[i，j]                                                                  Z[i,j,k]

基向量表达：

        常用的坐标系一般为笛卡尔坐标系，如U坐标系所示，向量i[1,0]，j[1,0]作为基向量组成笛卡尔坐标系，如下图所示以基向量i，j为参考坐标系，G向量可以表示为，

 其中G向量可以表示为如下所示

 基向量组成矩阵，形式可以是列向量也可以是行向量表达。如下图所示坐标系中

U坐标系基向量矩阵(列向量形式)表示为：

 在坐标系U下，V的基向量表示为:

 可视为变换后基向量在U坐标系下的表达，是一种线性变换，U坐标系下点(-1，2)变换后可表示为点(-1，4)，在V坐标系下，坐标可表示为(-1，2)，如下图所示

 变换

 

        在坐标系U(比如二维xy坐标系)下，对V的基向量的描述就是一种空间线性变换过程(旋转+缩放)称为变换

    变换本身就是对原有坐标系的变换

变换形式一般有两种：旋转和缩放

• 只发生旋转的矩阵：矩阵各元素数值归一化到[-1，1]区间
• 只发生缩放的矩阵：矩阵为对角矩阵

如下图所示：

有如下变换 

   

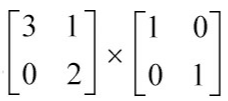
则其逆变换(恢复到变换(旋转+缩放)前的样子，表示为V的逆矩阵)为

原U坐标系下点G变换到V坐标系下的坐标G':

在U坐标系下：变换前G(0,-1)，变换后， G'(-1,-2)，在V坐标系下：G'(0,-1)

 相似矩阵

        已知，在U坐标系下，对U坐标做一个逆旋转90。的变换只需要乘以一个变换矩阵A(只做旋转不做缩放)，如下所示

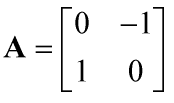
        那么在V坐标系下，如下图所示，我们也对V坐标系做一个逆旋转90。的变换，如何表示呢？能否继续用变换矩阵A呢？

        已知变换矩阵A是在U坐标系下的表达，而在V坐标系下，逆旋转90的变换矩阵是否等价A？

如下所示，在V坐标系下，存在向量v[-1，2]，对向量V做A变换得到如下所示

 此时可以发现在V坐标系下变换A除了对向量v做了旋转，同时还做了缩放，而我们只要求做逆时针旋转90的变换，所以在V坐标系下，逆旋转90的变换矩阵并不等于A，所以不能直接用矩阵A作用在V坐标系下。

那么在V坐标系下，逆时针旋转90的变换矩阵该如何表达？

已知

 设向量v是在V坐标系下的表达为v[-1，2]，基变换P得到U坐标系下V的基向量的表达，对向量 v[-1，2]通过如下过程做变换

 此时，可以得到在V坐标系下做逆时针旋转90。的变换矩阵表达为 B

综上，变换矩阵A和B其实为同一变换效果在不同坐标系下的表达，称A与B为相似矩阵

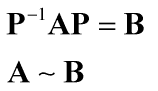
        相似矩阵A和B描述的是同一个变换过程。只是用于描述这一过程的基向量不一样。相似矩阵的用途：用通俗语言来讲，就是所谓把一个一般形式的新问题转化为一个已被解决过的“规范”问题，就像求解一元二次代数方程的时候我们把它化成一般形式然后套用求根公式一样。

        若两个矩阵相似，则这两个矩阵具有秩相等，行列式相等，迹相等，初等因子相等，特征值相等，特征多项式相等，等等一些很好的特性。所以当我们研究一个一般形式的矩阵的时候，如果可以找到与它相似的一些标准形式，就可以将任意矩阵的问题转化为一些固定形式的问题。比如对于可对角化的矩阵，可以研究与其相似的对角阵；对于一般的复数域上的矩阵，都可以转化为Jordan标准型。因为这些标准型具备与原矩阵相同的很多特性，而由于标准型的形式比较特殊，其特性更易于研究，并且由于标准型的形式是固定的，对其各种特性的研究有固定的套路可循。

行列式

假设矩阵A表示一种变换，det(A)≠0，则在二维、三维坐标下，分别表示面积和体积

   ,    

det(A):反映变换前后面积/体积的缩放程度和方向(det(A)正负)的变化

     

若det(A)=0，则反映了某一/n维被降维为零/线即被旋转至共面/线或缩放至0，使得面积或体积=0。如下所示

 例如：当A为2*3矩阵,其中列表示基向量。则表明变换A发生了降 维(有三个基向量，但用二维坐标表示，说明3个基向量存在相关)

特征向量

线性变换后原有的向量大多都发生了旋转+缩放，如下图向量G，G‘

 但也有部分向量在变换前后的方向仍保持不变，只做缩放，如下图所示变换

 其中有如下所示向量在变换前后的方向仍保持不变

                 

这些变换前后方向保持不变，只做缩放的变量称为变换A的特征向量，其对应的缩放值称为特征值，可表示为如下公式

注意：A为n阶矩阵即方阵，λ为特征值，α为特征向量

如下图所示

特征向量作为基向量 

如上图所示的两个特征向量，以这两个特征向量作为基向量的变换矩阵表示为P，P=[α1，α2]，其中α1，α2为特征向量，对应的特征值为λ1、λ2 ，如下图所示

 以特征向量为基向量的变换矩阵，在本文称为特征基变换。特征基变换P同变换A一样，都是起映射(旋转+缩放)原数据的作用，不过变换P可以将原始数据映射到其对应的特征向量方向上，且P的不同特征值(缩放量)对应的特征向量线性无关，可以使映射后的数据在各个特征基(不同特征值对应的特征向量)的方向上不相关，而普通变换A不能保证映射后的数据恰好在各个特征维度上从而保持不相关。

注意：

不同特征值(缩放量)对应的特征向量不一定正交，只有A是实对称矩阵时，且是A的不同特征值对应的特征向量才能两两正交。
正交：np.dot(a,b)=0
线性不相关：若x1a+x2b+x3c=0，只有x1=x2=x3=0时才成立，则a、b、c向量线性无关
线性相关：若x1a+x2b+x3c=0，只有x1、x2、x3存在非零解使式子成立，则a、b、c向量线性相关。
两向量的内积只是用来判断是否正交，不能用来作为是否线性相关的依据。

相关/不相关可以简单理解为：数据是否存在冗余。比如训练数据有3列特征，其中一列特征可又其余的两列特征组合表示，则说明该列特征是冗余的，进而训练数据可"删除"该列特征，做降维处理。

特征基用途

我们希望手里的训练的数据能用尽可能少的特征的表达样本信息，即减少冗余特征或者称为对训练数据提取特征，这样也能减少计算量。但真实的训练数据总是存在各种各样的问题，不能直接肉眼看出那些特征是冗余特征，所以需要有这样的一个变换P，能够使数据有选择的映射到部分正交基(特征基)上，这样既能使映射后的数据各个特征不相关，也能减少计算量(减少冗余特征)，从而方便训练数据。

矩阵对角化

∵

∴

上面的过程为相似对角化过程，对角化矩阵为缩放矩阵，只做缩放变换。

为什么要对角化矩阵？-计算方便 

 实对称矩阵性质

1、若A是实对称矩阵，则A可逆，且存在特征矩阵P，使得A可以被相似对角化：P-1AP

2、若A是实对称矩阵，对A的逆矩阵P[α1,α2,...,αn]施密特正交规范化得正交矩阵Q[β1,β2,...,βn]，由于实对称矩阵的特征向量P本身就是正交矩阵，所以只需对P规范化(单位化)处理即可，可满足,

规范化：向量除以向量模长

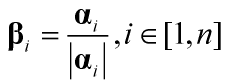
，注意：python中np.linalg.eig()在计算特征向量的过程中已对特征向量规范化了

协方差矩阵为对称矩阵，常被用来相似对角化。

正交矩阵性质

若Q为n阶矩阵，设Q=[β1,β2,...,βn]，满足（或），则称Q为正交矩阵

• β1,β2,...,βn为两两正交的规范向量组，

• |Q|=±1

• 特征值λ=±1

• 若Y=XQ，则|Y|=|X|

• ：正交矩阵的逆矩阵==正交矩阵的转置矩阵

      -》   

特征值分解矩阵

已知一个矩阵可分解为多个向量外积和的形式，如下图所示矩阵随机分解为如下

 如上所示的矩阵分解只是一个随意的分解过程并没有多么特殊。特征值分解矩阵其实也是这样的过程，有如下形式，不同的是其对角矩阵上的值为特征值只做缩放变换，左右矩阵称为酉矩阵，满足，为单位化正交矩阵。

矩阵特征值分解过程如下

已知存在

对特征向量矩阵P正交规范化得到Q，满足

注意：若A是实对称矩阵，则其不同特征值对应的特征向量组曾的矩阵P本身就是正交矩阵，此时只需对P规范化处理。

上面的过程称为相似对角化

而 的过程称为特征值分解矩阵，注意到要进行特征分解，矩阵A必须为方阵(因为需要对特征向量矩阵求逆矩阵，非方阵矩阵不可求逆)。

那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？

奇异值分解矩阵(SVD) 

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵必须为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为

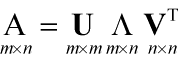
 SVD奇异值分解其对角矩阵上的值为特征值的平方根只做缩放变换，左右矩阵称为酉矩阵，均为单位化正交矩阵只做旋转变换。变换过程如下

 那么我们如何求出SVD分解后的U,,V这三个矩阵呢？

 设变换X是一个混合变换矩阵，可能包含旋转＋缩放，求解过程如下

奇异值分解性质

 对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。

也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。

其中k可以比n小很多，也就是一个大的矩阵A可以用三个小的矩阵 来表示。如下图所示

 由于这个重要的性质，SVD可以用于PCA降维(SVD的右奇异矩阵)，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。