[动态规划] leetcode 416. 分割等和子集

问题描述：

   分割等和子集：给你一个只包含正整数的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
  例子：输入nums = {1, 5, 11 , 5}; 输出true。

动态规划求解

  这是一个0-1背包问题的变种，也就是每种物品只能选择一次。与之对应的是完全背包问题，选择每种物品的数量是不限制的，可以与另一篇博文对照来看。将非空数组 nums，分为两部分，使得两部分的和相等，该问题等价于从数组中选择部分数字，使得其和等于数组总和的一半。特别的当数组总和sum为基奇数，不可能将数组拆成相等的两部分，直接返回false。
  令$dp[i][j]$表示，选择数组前$i$个元素，其和是否能为$j$。则有：
  当$j>=nums[i-1]$时， 可以选择不添加该元素直接得到j，或者由添加该元素得到j，即
$$dp[i][j]=dp[i-1][j]||dp[i-1][j-nums[i-1]]$$
   当$j<nums[i-1]$时，当前元素不可选择，否则会直接超出j，有
$$dp[i][j]=dp[i-1][j]$$
   特别的$dp[0][0]=1$，因为和为0只有一种情况：不选择任何元素。
   在本示例中有，$dp[2][6]=dp[1][6-nums[1]]||dp[1][6]=dp[1][1]||dp[1][6]=true$，返回值即为$dp[nums.length][sum/2]=dp[4][11]=true$。

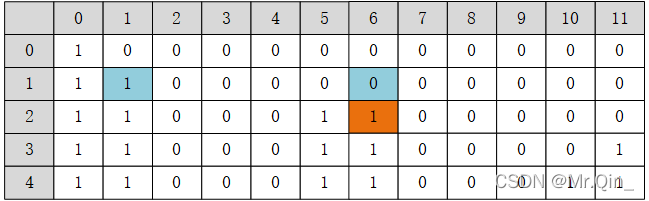
  程序实现需要编写两层循环，分别对应数组长度$i$和和$j$。需要注意的是$i$循环时从1开始，总数$j$循环时从0开始，第$i$元素的值为$nums[i-1]$。运行结果为33 ms 42.4 MB。

class Solution {
    public boolean canPartition(int[] nums) {
        int len = nums.length;
        int sum = 0;
        for(int num : nums){
            sum += num;
        }
        if(sum % 2 != 0){
            return false;
        }
        int target = sum /2;
        boolean[][] dp = new boolean[len +1][target + 1];
        dp[0][0] = true;
        for (int i = 1; i <=len; i++) {
            for (int j = 0; j <=target; j++) {
                if(nums[i-1] <= j){
                    dp[i][j] = dp[i - 1][j] || dp[i-1][j - nums[i-1]];
                }else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[len][target];
    }
}

空间复杂度优化

考虑到$dp[i][j]$的值仅与第$i-1$行有关系，可以采用滚动数组的思想来降低空闲复杂度。具体的，只维护一维的$dp$数组，其状态更新关系为：
$$dp[j]=dp[j-nums[i-1]]+dp[j]$$

  需要注意的是，第二层的循环我们需要从大到小计算，因为如果我们从小到大更新 $dp$值，那么在计算 $dp[j]$ 值的时候， $dp[j-nums[i-1]]$已经是被更新过的状态，不再是上一行的 $dp$ 值。运行结果为 19 ms 39.6 MB，可以看到空间使用情况有所降低。

class Solution {
    public boolean canPartition(int[] nums) {
        int len = nums.length;
        int sum = 0;
        for(int num : nums){
            sum += num;
        }
        if(sum % 2 != 0){
            return false;
        }
        int target = sum /2;
        boolean[] dp = new boolean[target + 1];
        dp[0] = true;
        for (int i = 1; i <=len; i++) {
            for (int j = target; j >=nums[i-1]; j--) {
                    dp[j] = dp[j] || dp[j - nums[i-1]];
            }
        }
        return dp[target];
    }
}