齐次坐标

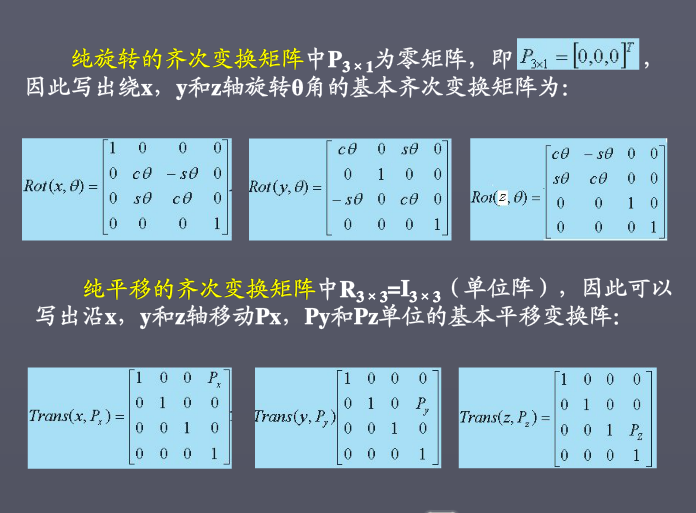
计算机图形学中常用的齐次坐标

“齐次坐标表示是计算机图形学的重要手段之一，它既能够来明确区分向量和点同时也更易于进行仿射（线性）几何变换”———F.S.Hill

定义：一般来说，以N+1维矢量表达N维矢量的方法称为齐次坐标表示法。

在三维直角坐标系中，一个点可以表示为[X,Y,Z]T(T表示转置)，它的齐次坐标就是[wX,wY,wZ,w]T,其中w为非零整数。可以看出w不同，一个点的齐次坐标的表达不唯一。齐次坐标不仅可以表示点的位置，还可以用来规定矢量的方向，即第四个元素直接设为0（前面的坐标就不用乘了），即[X,Y,Z,0].

举个例子
有一个点记作r=[x,y,z],沿向量t=[t1,t2,t3]平移，平移结果为

r+t=[x+t1,y+t2,z+t3]

如果将r化为齐次坐标r=[x,y,z，1]那么我们可以找到一个4x4的矩阵来实现平移

则r.tr+t=[x+t1,y+t2,z+t3,1]将加法运算统一化为矩阵乘法

这样做有一个好处：
一个坐标系变换至另一个坐标系的齐次变换矩阵等于依次经历中坐标系各齐次变换矩阵的乘积，最终所有变换的结果就是一个矩阵大大减少了计算量和存储量