理论基础
说实话,讲理论基础实在不是我的强项,但是还是得硬着头皮来讲,希望我的讲解不至于晦涩难懂。
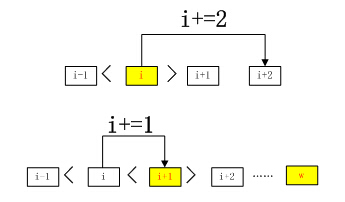
非极大值抑制,简称为NMS算法。是一种获取局部最大值的有效方法。在3领域中,假设一个行向量的长度为w,从左向右,由第一个到第w个和其3领域中的数值进行比对。
如果某个i大于i+1并且小于i-1,则其为一个绝不最大值,同时也就意味着i+1不是一个局部最大值,所以将i移动2个步长,从i+2开始继续向后进行比较判断。如果某个i不满足上述条件,则将i+1,继续对i+1进行比对。当比对到最后一个w时,直接将w设置为局部最大值。算法流程如下图所示。
应用范围

针对该问题有3种传统的解决思路。
第一种,选取好多矩形框的交集,即公共区域作为最后的目标区域。
第二种,选取好多矩形框的并集,即所有矩形框的最小外截矩作为目标区域。当然这里也不是只要相交就直接取并集,需要相交的框满足交集占最小框的面积达到一定比例(也就是阈值)才合并。
第三种,也就是本文的NMS,简单的说,对于有相交的就选取其中置信度最高的一个作为最后结果,对于没相交的就直接保留下来,作为最后结果。
总体来说,3种处理思路都各有千秋,不能一概评论哪种好坏。各种顶会论文也会选择不同的处理方法。
程序实现
本文提供了nonMaximumSuppression的c语言,c++,M语言,三个版本。
其中,c语言版本为opencv的源码这里摘出并进行相关的注释。sort为排序函数,这里是最基本的选择排序算法的实现。nonMaximumSuppression为具体非极大值抑制的实现。
static void sort(int n, const float* x, int* indices)
{
// 排序函数,排序后进行交换的是indices中的数据
// n:排序总数// x:带排序数// indices:初始为0~n-1数目
int i, j;
for (i = 0; i < n; i++)
for (j = i + 1; j < n; j++)
{
if (x[indices[j]] > x[indices[i]])
{
//float x_tmp = x[i];
int index_tmp = indices[i];
//x[i] = x[j];
indices[i] = indices[j];
//x[j] = x_tmp;
indices[j] = index_tmp;
}
}
}
int nonMaximumSuppression(int numBoxes, const CvPoint *points,
const CvPoint *oppositePoints, const float *score,
float overlapThreshold,
int *numBoxesOut, CvPoint **pointsOut,
CvPoint **oppositePointsOut, float **scoreOut)
{
// numBoxes:窗口数目// points:窗口左上角坐标点// oppositePoints:窗口右下角坐标点
// score:窗口得分// overlapThreshold:重叠阈值控制// numBoxesOut:输出窗口数目
// pointsOut:输出窗口左上角坐标点// oppositePoints:输出窗口右下角坐标点
// scoreOut:输出窗口得分
int i, j, index;
float* box_area = (float*)malloc(numBoxes * sizeof(float)); // 定义窗口面积变量并分配空间
int* indices = (int*)malloc(numBoxes * sizeof(int)); // 定义窗口索引并分配空间
int* is_suppressed = (int*)malloc(numBoxes * sizeof(int)); // 定义是否抑制表标志并分配空间
// 初始化indices、is_supperssed、box_area信息
for (i = 0; i < numBoxes; i++)
{
indices[i] = i;
is_suppressed[i] = 0;
box_area[i] = (float)( (oppositePoints[i].x - points[i].x + 1) *
(oppositePoints[i].y - points[i].y + 1));
}
// 对输入窗口按照分数比值进行排序,排序后的编号放在indices中
sort(numBoxes, score, indices);
for (i = 0; i < numBoxes; i++) // 循环所有窗口
{
if (!is_suppressed[indices[i]]) // 判断窗口是否被抑制
{
for (j = i + 1; j < numBoxes; j++) // 循环当前窗口之后的窗口
{
if (!is_suppressed[indices[j]]) // 判断窗口是否被抑制
{
int x1max = max(points[indices[i]].x, points[indices[j]].x); // 求两个窗口左上角x坐标最大值
int x2min = min(oppositePoints[indices[i]].x, oppositePoints[indices[j]].x); // 求两个窗口右下角x坐标最小值
int y1max = max(points[indices[i]].y, points[indices[j]].y); // 求两个窗口左上角y坐标最大值
int y2min = min(oppositePoints[indices[i]].y, oppositePoints[indices[j]].y); // 求两个窗口右下角y坐标最小值
int overlapWidth = x2min - x1max + 1; // 计算两矩形重叠的宽度
int overlapHeight = y2min - y1max + 1; // 计算两矩形重叠的高度
if (overlapWidth > 0 && overlapHeight > 0)
{
float overlapPart = (overlapWidth * overlapHeight) / box_area[indices[j]]; // 计算重叠的比率
if (overlapPart > overlapThreshold) // 判断重叠比率是否超过重叠阈值
{
is_suppressed[indices[j]] = 1; // 将窗口j标记为抑制
}
}
}
}
}
}
*numBoxesOut = 0; // 初始化输出窗口数目0
for (i = 0; i < numBoxes; i++)
{
if (!is_suppressed[i]) (*numBoxesOut)++; // 统计输出窗口数目
}
*pointsOut = (CvPoint *)malloc((*numBoxesOut) * sizeof(CvPoint)); // 分配输出窗口左上角坐标空间
*oppositePointsOut = (CvPoint *)malloc((*numBoxesOut) * sizeof(CvPoint)); // 分配输出窗口右下角坐标空间
*scoreOut = (float *)malloc((*numBoxesOut) * sizeof(float)); // 分配输出窗口得分空间
index = 0;
for (i = 0; i < numBoxes; i++) // 遍历所有输入窗口
{
if (!is_suppressed[indices[i]]) // 将未发生抑制的窗口信息保存到输出信息中
{
(*pointsOut)[index].x = points[indices[i]].x;
(*pointsOut)[index].y = points[indices[i]].y;
(*oppositePointsOut)[index].x = oppositePoints[indices[i]].x;
(*oppositePointsOut)[index].y = oppositePoints[indices[i]].y;
(*scoreOut)[index] = score[indices[i]];
index++;
}
}
free(indices); // 释放indices空间
free(box_area); // 释放box_area空间
free(is_suppressed); // 释放is_suppressed空间
return LATENT_SVM_OK;
}
c++版本程序如下所示,根据opencv源码改编,vs2010实测运行完美。由于c和c++版本基本一个思路,因此将这两个的思路一起讲解。
整体程序分为两部分,sort函数主要实现候选框的置信度从高到低的排序,是基于基本的选择排序实现。nonMaximumSuppression主要实现非极大值抑制算法。算法思路为,先根据候选框的points 和oppositePoints 求出每个候选框的面积box_area,并将标签is_suppressed全部置为0。通过一个二重for循环将所有的候选框进行比对,这里的循环是从置信度最高的窗口进行比对,每层外循环中置信度最高的保留,其余的只要大于规定阈值overlapThreshold就舍弃,不大于阈值的保留下来。最终输出NMS处理后的结果。
static void sort(int n, const vector<float> x, vector<int> indices)
{
// 排序函数,排序后进行交换的是indices中的数据
// n:排序总数// x:带排序数// indices:初始为0~n-1数目
int i, j;
for (i = 0; i < n; i++)
for (j = i + 1; j < n; j++)
{
if (x[indices[j]] > x[indices[i]])
{
//float x_tmp = x[i];
int index_tmp = indices[i];
//x[i] = x[j];
indices[i] = indices[j];
//x[j] = x_tmp;
indices[j] = index_tmp;
}
}
}
int nonMaximumSuppression(int numBoxes, const vector<CvPoint> points,const vector<CvPoint> oppositePoints,
const vector<float> score, float overlapThreshold,int& numBoxesOut, vector<CvPoint>& pointsOut,
vector<CvPoint>& oppositePointsOut, vector<float> scoreOut)
{
// 实现检测出的矩形窗口的非极大值抑制nms
// numBoxes:窗口数目// points:窗口左上角坐标点// oppositePoints:窗口右下角坐标点// score:窗口得分
// overlapThreshold:重叠阈值控制// numBoxesOut:输出窗口数目// pointsOut:输出窗口左上角坐标点
// oppositePoints:输出窗口右下角坐标点// scoreOut:输出窗口得分
int i, j, index;
vector<float> box_area(numBoxes); // 定义窗口面积变量并分配空间
vector<int> indices(numBoxes); // 定义窗口索引并分配空间
vector<int> is_suppressed(numBoxes); // 定义是否抑制表标志并分配空间
// 初始化indices、is_supperssed、box_area信息
for (i = 0; i < numBoxes; i++)
{
indices[i] = i;
is_suppressed[i] = 0;
box_area[i] = (float)( (oppositePoints[i].x - points[i].x + 1) *(oppositePoints[i].y - points[i].y + 1));
}
// 对输入窗口按照分数比值进行排序,排序后的编号放在indices中
sort(numBoxes, score, indices);
for (i = 0; i < numBoxes; i++) // 循环所有窗口
{
if (!is_suppressed[indices[i]]) // 判断窗口是否被抑制
{
for (j = i + 1; j < numBoxes; j++) // 循环当前窗口之后的窗口
{
if (!is_suppressed[indices[j]]) // 判断窗口是否被抑制
{
int x1max = max(points[indices[i]].x, points[indices[j]].x); // 求两个窗口左上角x坐标最大值
int x2min = min(oppositePoints[indices[i]].x, oppositePoints[indices[j]].x); // 求两个窗口右下角x坐标最小值
int y1max = max(points[indices[i]].y, points[indices[j]].y); // 求两个窗口左上角y坐标最大值
int y2min = min(oppositePoints[indices[i]].y, oppositePoints[indices[j]].y); // 求两个窗口右下角y坐标最小值
int overlapWidth = x2min - x1max + 1; // 计算两矩形重叠的宽度
int overlapHeight = y2min - y1max + 1; // 计算两矩形重叠的高度
if (overlapWidth > 0 && overlapHeight > 0)
{
float overlapPart = (overlapWidth * overlapHeight) / box_area[indices[j]]; // 计算重叠的比率
if (overlapPart > overlapThreshold) // 判断重叠比率是否超过重叠阈值
{
is_suppressed[indices[j]] = 1; // 将窗口j标记为抑制
}
}
}
}
}
}
numBoxesOut = 0; // 初始化输出窗口数目0
for (i = 0; i < numBoxes; i++)
{
if (!is_suppressed[i]) numBoxesOut++; // 统计输出窗口数目
}
index = 0;
for (i = 0; i < numBoxes; i++) // 遍历所有输入窗口
{
if (!is_suppressed[indices[i]]) // 将未发生抑制的窗口信息保存到输出信息中
{
pointsOut.push_back(Point(points[indices[i]].x,points[indices[i]].y));
oppositePointsOut.push_back(Point(oppositePoints[indices[i]].x,oppositePoints[indices[i]].y));
scoreOut.push_back(score[indices[i]]);
index++;
}
}
return true;
}
matlab版本的程序只有1个函数nms。
程序参数说明:
boxes为输入的矩形框,overlap为设置的一个阈值,pick为NMS处理后的输出矩阵在boxes中的对应位置。
box中存放的数据格式如下:
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | 第六列 | …… |
左上角x | 左上角y | 右下角x | 右下角y | 置信度 | 置信度 | …… |
| …… | …… | …… | …… | …… | …… | …… |
程序整体思路:
先将box中的数据分别存入x1,y1,x2,y2,s中,分别为坐标和置信度,算出每个框的面积,存入area,基于置信度s,从小到达进行排序,做一个while循环,取出置信度最高的,即排序后的最后一个,然后将该框进行保留,存入pick中,然后和其他所有的框进行比对,大于规定阈值就将别的框去掉,并将该置信度最高的框和所有比对过程,大于阈值的框存入suppress,for循环后,将I中满足suppress条件的置为空。直到I为空退出while。
简单的说,就是比如图像中有4个位置出现框的交叉重叠,每一次while循环都会去掉一个位置的交叉框,留下置信度最高的那个。while循环负责4个位置的循环,for循环负责每个位置交叉框的循环。
function pick = nms(boxes, overlap)
% pick = nms(boxes, overlap)
% Non-maximum suppression.
% Greedily select high-scoring detections and skip detections
% that are significantly covered by a previously selected detection.
if isempty(boxes)
pick = [];
else
x1 = boxes(:,1); %所有候选框的左上角顶点x
y1 = boxes(:,2); %所有候选框的左上角顶点y
x2 = boxes(:,3); %所有候选框的右下角顶点x
y2 = boxes(:,4); %所有候选框的右下角顶点y
s = boxes(:,end); %所有候选框的置信度,可以包含1列或者多列,用于表示不同准则的置信度
area = (x2-x1+1) .* (y2-y1+1);%所有候选框的面积
[vals, I] = sort(s); %将所有候选框进行从小到大排序,vals为排序后结果,I为排序后标签
pick = [];
while ~isempty(I)
last = length(I); %last代表标签I的长度,即最后一个元素的位置,(matlab矩阵从1开始计数)
i = I(last); %所有候选框的中置信度最高的那个的标签赋值给i
pick = [pick; i]; %将i存入pick中,pick为一个列向量,保存输出的NMS处理后的box的序号
suppress = [last]; %将I中最大置信度的标签在I中位置赋值给suppress,suppress作用为类似打标志,
%存入suppress,证明该元素处理过
for pos = 1:last-1 %从1到倒数第二个进行循环
j = I(pos); %得到pos位置的标签,赋值给j
xx1 = max(x1(i), x1(j));%左上角最大的x(求两个方框的公共区域)
yy1 = max(y1(i), y1(j));%左上角最大的y
xx2 = min(x2(i), x2(j));%右下角最小的x
yy2 = min(y2(i), y2(j));%右下角最小的y
w = xx2-xx1+1; %公共区域的宽度
h = yy2-yy1+1; %公共区域的高度
if w > 0 && h > 0 %w,h全部>0,证明2个候选框相交
o = w * h / area(j);%计算overlap比值,即交集占候选框j的面积比例
if o > overlap %如果大于设置的阈值就去掉候选框j,因为候选框i的置信度最高
suppress = [suppress; pos];%大于规定阈值就加入到suppress,证明该元素被处理过
end
end
end
I(suppress) = [];%将处理过的suppress置为空,当I为空结束循环
end
end
这里给出2个最简单基本的c++和matlab相应的测试程序。
c++测试程序如下:
int main()
{
Mat image=Mat::zeros(600,600,CV_8UC3);
int numBoxes=4;
vector<CvPoint> points(numBoxes);
vector<CvPoint> oppositePoints(numBoxes);
vector<float> score(numBoxes);
points[0]=Point(200,200);oppositePoints[0]=Point(400,400);score[0]=0.99;
points[1]=Point(220,220);oppositePoints[1]=Point(420,420);score[1]=0.9;
points[2]=Point(100,100);oppositePoints[2]=Point(150,150);score[2]=0.82;
points[3]=Point(200,240);oppositePoints[3]=Point(400,440);score[3]=0.5;
float overlapThreshold=0.8;
int numBoxesOut;
vector<CvPoint> pointsOut;
vector<CvPoint> oppositePointsOut;
vector<float> scoreOut;
nonMaximumSuppression( numBoxes,points,oppositePoints,score,overlapThreshold,numBoxesOut,pointsOut,oppositePointsOut,scoreOut);
for (int i=0;i<numBoxes;i++)
{
rectangle(image,points[i],oppositePoints[i],Scalar(0,255,255),6);
char text[20];
sprintf(text,"%f",score[i]);
putText(image,text,points[i],CV_FONT_HERSHEY_COMPLEX, 1,Scalar(0,255,255));
}
for (int i=0;i<numBoxesOut;i++)
{
rectangle(image,pointsOut[i],oppositePointsOut[i],Scalar(0,0,255),2);
}
imshow("result",image);
waitKey();
return 0;
}
boxes=[200,200,400,400,0.99;
220,220,420,420,0.9;
100,100,150,150,0.82;
200,240,400,440,0.5];
overlap=0.8;
pick = nms(boxes, overlap);
figure;
for (i=1:size(boxes,1))
rectangle('Position',[boxes(i,1),boxes(i,2),boxes(i,3)-boxes(i,1),boxes(i,4)-boxes(i,2)],'EdgeColor','y','LineWidth',6);
text(boxes(i,1),boxes(i,2),num2str(boxes(i,5)),'FontSize',14,'color','b');
end
for (i=1:size(pick,1))
rectangle('Position',[boxes(pick(i),1),boxes(pick(i),2),boxes(pick(i),3)-boxes(pick(i),1),boxes(pick(i),4)-boxes(pick(i),2)],'EdgeColor','r','LineWidth',2);
end
axis([0 600 0 600]);
实验结果
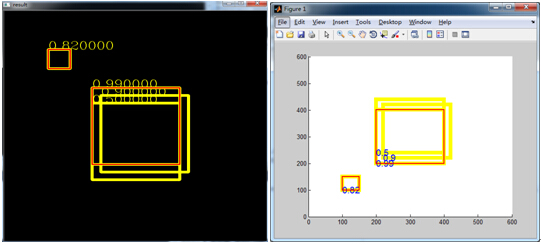
c++和Matlab的测试结果如下所示,其中,红色框为经过NMS处理后的结果,黄色框为原始的输入框。从图中可以看出,经过NMS处理后的候选框中,在重叠部分大于规定阈值的都被舍弃,只保留其中置信度最高的一个,而对于没有重叠的框,不管其置信度多少,都直接保留下来。
注意,在matlab,opencv里面图像左上角为坐标原点,而本文在matlab中是单纯画图,此时图像左下角为坐标原点,所以同样的坐标,两幅图效果有所区别。
本文所有程序github下载链接https://github.com/watersink/nonMaximumSuppression,希望本文对大家有帮助。








 本文详细介绍了非极大值抑制(NMS)算法原理及其实现,包括C、C++和MATLAB三种语言版本的代码,并通过实例展示了NMS如何有效筛选重叠的候选区域。
本文详细介绍了非极大值抑制(NMS)算法原理及其实现,包括C、C++和MATLAB三种语言版本的代码,并通过实例展示了NMS如何有效筛选重叠的候选区域。
















 578
578

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








