因果推断大集合 从0-1的因果知识(一篇)

引言
文章介绍了几类经典的因果推断算法(metalearning、因果森林、连续因果变量、PID、小样本、帕累托最优等)，在实际营销场景可结合具体算法快速部署，结果评估中结合AA波动、AB显著差异等方法确定效果的持续稳定性。

1.背景

随着人工智能的发展，越来越多学者开始认识到因果推断对于克服现有人工智能方法/技术在抽象、推理和可解释性等方面的不足具有重要意义。正如图灵奖得奖者Judea Pearl在新作《The Book of Why》一书中提出的 “因果关系之梯”，他把因果推断分成三个层面，第一层是“关联”；第二层是“干预”；第三层是“反事实推理”。目前大部分机器学习模型还处在第一层级，仅仅实现了对历史数据的“曲线拟合”，这就导致：一是解释性差，拟合背后的作用机理处于黑盒状态；二是泛化性差，拟合得到规律只适用于训练数据。而因果推断方法能让我们站上第二、三层级，从而实现更好的解释性和泛化性，这也是因果推断在机器学习领域逐步兴起的一大原因。（因果推断可以补充机器学习方法过程中没有解释清楚的问题，一般ML都是解释X-> Y，但是没有说明白 Y-> X）

因果推断的目标是发现变量/事物背后的因果关系。随机控制实验(RCTs)是发现因果关系的传统方法。由于实验技术局限和实验耗费代价巨大等原因，越来越多的因果推断领域学者希望通过观察数据(observe data)推断变量之间的因果关系，已成为当前因果推断领域的研究热点。但实施存在两个难点：一是数据缺失的问题(反事实求解)，从观察数据中我们只能得到fatual outcomes，无法得知counterfactual outcomes；二是偏差的问题(选择偏差、混淆)，收集observational data的过程中，treatments并不是随机分配的，即存在confounders，如果仅根据observational data去估计因果效应，得到的因果效应结果是有偏的。机器学习预测未来，因果推断改变未来。
因果推断解决的问题可以分成两类：
因果推断和机器学习其实是可以互相帮助的。在机器学习帮助因果推断方面，针对上述数据缺失的问题，引入机器学习模型可以大大提高反事实预测的准确率；而通过deep representation learning的方法，则可以对confounder variables进行调整，从而解决偏差的问题。在因果推断帮助机器学习方面，当前的机器学习方法追求的是预测的高精度（accuracy），引入因果推断则可以解决正确性（correctness）和可解释性（interpretability）的问题。
举个例子，一个CVR响应模型（respond model）能预估给某个用户投放广告后的转化率，但实际上即使不投放广告用户也可能会发生转化。至于这个用户是否是因为看到广告才转化的、或者说多大程度上是因为看到广告转化的，CVR响应模型无法回答这个问题。业务上，自然不想再花钱去投放广告给这种不需要曝光广告也能转化的用户（不追求转化的品牌广告除外）。
如果有另一个模型能够预估广告对用户的转化意愿产生多大的影响（uplift CVR），意味着可以把广告预算分配给更需要的用户（花在刀刃上），进而提高整体效益。这就是因果推断要做的事，这种模型称为 uplift 模型(uplift model)，强调因果性。
首先以生活中的几个常见例子进行展开
●比如 吸烟是否会导致肺癌吸？烟的人里有肺癌患者，不吸烟的人里也有肺癌患者，这个经典的问题经过漫长的验证。
●比如 上大学是否会带来更多收入？直觉上我们认为高等教育会增加个人收入，但我们却很难说清楚没有上过大学的人如果上了大学会增加多少收入，同时我们也有看到没上过大学也能赚大钱的人。
●比如，在智能营销领域中，给用户发了优惠券以刺激购买转化，但事实上，部分用户可能不需要优惠券也能发生购买转化，如何在给定的平台预算下最大化收益呢？怎么预估用户因为券而增加多大购买意愿的呢？
●比如，如果你当初做了另一个选择，现在的自己会不会有什么不一样…
因果推断 要做的事情就是：预估一种干预因素（treatment）对结果（outcome）的影响（treatment effect）

1.1 辛普森悖论

首先，考虑一个与现实情况很相关的例子：针对某种新冠病毒 COVID-27，假设有两种疗法：方案 A 和方案 B，B 比 A 更稀缺（耗费的医疗资源更多），因此目前接受方案 A 的患者与接受方案 B 的患者比例约为：73%/27%。想象一下你是一名专家，需要选择其中一种疗法，而这个国家只能选择这一种疗法，那么问题来了，如何选择才能尽量少的减少死亡？
假设你有关于死于 COVID-27 的人的百分比数据（表1）。他们所接受的治疗是与病情的严重程度相关的，mild 表示轻症，severe 表示重症。在表 1 中，可以看到接受方案的人中总共有 16% 的人死亡，而接受 B 的死亡率是 19%，我们可能会想更贵的治疗方案 B 比便宜的治疗方案 A 的死亡率要更高，这不是离谱吗。然而，当我们按照轻症、重症分别来看（Mild 列和 Severe 列），情况确是相反的。在这两种情况下，接受 B 的死亡率比 A 都要低。
此时神奇的悖论就出现了。如果从全局视角来看，我们更倾向于选择 A 方案，因为 16%<19%。但是，从 mild 和 severe 视角来看，我们都更倾向于方案 B，因为 10%<15%，20%<30%。

1.2 相关性!=因果性

我们观察到公鸡打鸣（事件X）和太阳升起（事件Y）总是同时发生，可以说X和Y具有相关性。
如果我们把公鸡杀了（干预X），太阳就再也不升起了（观察Y），说明公鸡打鸣和太阳升起是因果关系，即“X → Y”。
如果我们把公鸡杀了（干预X），太阳依然照常升起（观察Y），说明公鸡打鸣不是太阳升起的原因，即“并非 X → Y”。
如果我们把公鸡关小黑屋里，相当于把太阳遮住（干预Y），公鸡就不打鸣了（观察X），说明“Y → X”。
如果我们把公鸡关小黑屋里（干预Y），公鸡早上依然打鸣（观察X），说明“并非 Y → X”。

1.3 营销四象限

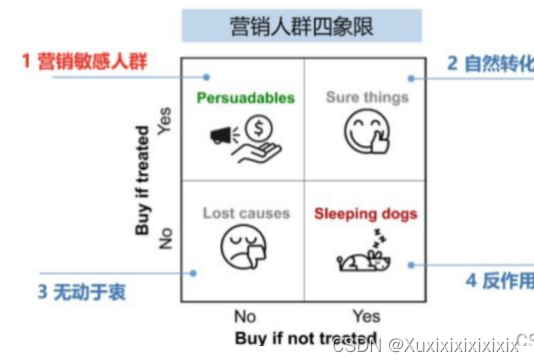
●persuadables: 不发券就不购买、发券才会购买的人群，即优惠券敏感人群
●sure thing：无论是否发券，都会购买，自然转化
●lost causes：无论是否发券都不会购买，这类用户实在难以触达到，直接放弃
●sleeping dogs：与persuadables相反，对营销活动比较反感，不发券的时候会有购买行为，但发券后不会再购买。

2.因果推断介绍

因果推断的根本问题可以分为两类，一个是因果关系发现，一个是因果效应评估；前者是找到T与Y，后者是衡量T改动对Y带来的影响，一般情况下我们是知道T和Y的先验，因此重点介绍后者；因果效应评估根据应用场景可以分为，给定观测数据(observed data、RCT)下的效应评估，如:拿到哇哈哈近一年的汽水销量数据与价格变动数据后，分析汽水价格对汽水销量的影响(因果效应)，总结为对已发生事情的分析。
●因果关系发现 （Causal Discovery）：从数据中发掘哪些变量之间存在因果关系，谁是因、谁是果。
●因果效应评估 （Causal Effect Estimatation）：评估一个变量变化后能多大程度影响另外一个变量。
另一种时，预估改变汽水价格为一定值时，汽水销量的改变，为对未来潜在结果的预估；前者是后者的前置条件。当前流行的两类因果推断 框架为因果图、潜在因果模型。其中潜在因果模型可以很好的与ML相结合，实际应用较多。常见的因果推断框架有结构方程模型 structural equation modeling 和Rubin因果模型 Rubin causal model。
综上，对因果推断的定义被描述为：
●推论得出“某事是（或可能是）其他事情的原因”这一结论。
●通过确定原因与效果的共变性（ covariation），前因后果的时序性，以及排除其它可能的替代原因，从而识别出现象的一个或多个原因。
通常情况下因果推断的过程，首先是提出一个假说，然后进行统计学假设检验来验证。这种统计学推断有助于判断数据是由偶然性（随机变化）引起的，还是确实相关（并测量相关性的强弱）。然而，相关不意味着因果，因此还需使用其他方法来推断其因果关系。
数据格式：是这样的三元组，<X，W，Y>，X是特征，W是施加的treatment，Y是outcome

2.1 因果推断的常见定义

2.2 因果性的常见谬误

预测场景下的常见数据训练偏差问题：

2.3 因果推断的流程

2.3.1 数据类型

观测数据、随机实验数据、观测数据+随机实验数据

2.3.2 去偏差

对于观测数据进行因果推断时，存在混淆变量X对T与Y均产生影响，直接计算会导致偏差结论 ，此时为解决混淆带来的影响需要进行去混淆;例如，研究汽水价格对销量影响时，需要考虑气温、流行趋势等高级特征即为混淆。如不考虑会导致得出错误的价格高销量便会降低的结论
因果推断的核心问题1）missing counterfactuals；2）imbalance covariates distribution under different intervention。只有知道了各种干预下的结果，才能计算出不同干预之间的因果效应。为了准确的估计反事实，需要解决由于混淆变量引起的不同干预下，样本特征分布不一致的问题，否则会具有selection bias，同时会带来估计的高方差。

1.re-weighting(权重更新方法)

对与观测数据中实验组和对照组数据分布的gaps，通过重新赋值权重得到weak 的观测数据进行总体因果数据评估，选择偏差:我们观察的数据中，策略分配与样本的其他变量是相关的。样本权重更新是一种有效的方法。它通过给每一个样本分配不同的权重，这样生成的样本集合中，试验组和对照组的分布是类似的。
具体方法：逆倾向得分权重（ Inverse propensity weighting(IPW)），也称作逆策略概率权重（inverse probability of treatment weighting(IPTW)）\Covariate balancing propensity score (CBPS)，协变量平衡倾向得分方法\the covariate balancing generalized propensity score (CBGPS) ，又来处理策略是连续值的情况;Data-Driven Variable Decomposition 算法是为了区分混杂变量、调整变量，同时消除不相关的变量而提出的.
具体算法介绍如下：
●sample re-weighting
它通过给每一个观测样本分配不同的权重，这样生成的样本集合中，试验组和对照组的分布是类似的；其中实验组可认为应该方案A的，对照组认为应用方案B的；By assigning appropriate weight to each unit in the observational data, a pseudo-population can be created on which the distributions of the treated group and control group are similar
通过对观测数据中的样本给予适当权重后生产出实验组和对照组相似的‘新’数据，作为‘新’的观察数据
●balancing score（平衡分）
权重得分，满足，其中W为应用的treatment，x为背景变量，常用的平衡分包括：b(x)=x(给定变量下的权重),Peopensity score（倾向性得分）
●Propensity score（倾向性得分）
定义为给定背景变量X后，样本选择treatment的概率，e.g.实验中的老年人选择A方案的概率
Balancing scores that incorporate propensity score are the most common approach
●IPW(Inverse propensity weighting、IPTW 逆倾向得分权重)
认为权重为,其中w为实验策略，仅取0，1，1代表实验组，0代表对照组，e(x):倾向得分，设想如果样本为1，则权重为1/e(x),倾向分越高权重越低，来平衡样本选择过多的影响，由前式：=>推导过程带入r为展开：化简，r中的w只取0，1.前半部分，w=0的部分没了，后半部分类似，化简后即可。当取1或0时即与上式子一致了由于平衡分预测准确度问题，导致依赖，因此提出基于倾向得分与结果回归模型的样本权重(Doubly Robust estimator，DR、sAugmented IPW，AIPW )分别是实验组与对照组回归模型的预估结果，解释为实验组与对照组的差异加上实验组或对照组真实结果与预测结果差距的IPTW加权【相当于，预测的偏差加上真值的偏差，拓宽倾向得分仅考虑选择偏差，协变量也被考虑在内时候为（Covariate balancing propensity score (CBPS)）及扩展为变量的 covariate balancing generalized propensity score (CBGPS)
●Confounder balancing 混杂平衡
The aforementioned sample re-weighting methods could achieve balance in the sense that the observed variables are considered equally as confounders.如果将观测变量都认为是混淆的话，通过权重调整是可以实现样本平衡的，实际中会出现只影响结果的可调整变量(adjustment variables)、无关变量(irrelevant variables)，调整adjustment variables可以帮助减少消减变成并不能去除偏差，而调整无关变量可能会导致过拟合现象。认为观测变量
oData-Driven Variable Decomposition (D2VD) 用于区分混淆和调整变量，减少无关变量

2.stratification（分层方法 subclassification or blocking）

与权重更新方式类似，通过调整观测数据将其分为‘同质’的子块后来调整实验组与对照组的gaps，达到每个子组内的实验组与对照组的X是一致的，这时的每组数据可以认为是全量数据在RCT下的结果，通过计算每个子快的CATE，加权平均后得到无偏的估计效果
主要问题为：如何分层和分层后如何估计ATE
主要介绍：1.分层加权统计相比较直接计算时偏差更小；2.等频率分组方法，利用’倾向分’(样本背后联合分布出现的概率)进行同倾向分的分组

3.Matching based(匹配方法)

主要解决减少选择偏差的基础上，求解反事实的方法。大体思路可认为是，对于给定的策略w和实验组样本i，反事实是中通过匹配方法找到对照组中i的临近集合，通过求解临近集合的观测结果均值得到i反事实结果
主要问题为：如何找到临近集合进行匹配，距离度量是什么
●度量距离
1.基于倾向得分的映射:公示为,其中e为倾向性得分
2.基于预知得分(prognosis score)
●匹配方法
1.最近邻匹配
2.caliper匹配
3.分层匹配
4.核匹配

4.tree-based

决策树是一种用于分类或者回归的无参数监督学习算法，决策树的目标是通过数据推导出简单的决策规则用以创建一个可以预测目标变量值的模型。
总体来说，就是我们虽然也是构建决策树，但是不是为了预测一个新的样本的目标变量，只是为了得到树的结构，然后基于这个树的结构自然而然的将整个数据集划分出很多子群，然后评估各个子群的策略效果，最后进行加权平均即可。
●贝叶斯加权回归树(BART)
算法的基本元素是贝叶斯回归树，模型的优化过程是使用蒙特卡洛随机模拟和贝叶斯后验来搞定的，而且不用设置参数，是维度自适应对样本就行了分层，或者说对样本进行了匹配，同一个叶子结点的样本为近邻群体，实现了分层或者匹配紧邻的目的；然后与前两种因果推断方法(分层和匹配)类似的加权求平均来评估ATE。然后上面介绍了好多这种方法的优点，其实主要就是无参数，自适应，集成方法准确度高。

5.representation-based

因果推断问题转化为领域适应问题，观测数据可能有偏，导致模型对反事实的预估效果较差导致
1.均衡表示学习：TARNet/CFR
2.局部相似表示学习：SITE
3.去工具变量 表示学习
4.基于表示学习的匹配方法

6.multi-task learning

应用多任务学习的本质依然是通过机器学习得到精准的模型来估计反事实结果，那么对于选择性偏差问题，我们采用基于倾向得分的dropout 方法来缓解。做过神经网络的同学应该比较熟悉dropout 方法，就是一种网络中常见的降低过拟合的正则化方法，原理类似于随机抽样，但是在传统的神经网络中，dropout 系数是一个我们提前设定的超参数，对每一个样本都是一样的，在这里的dropout 系数是根据倾向得分个性化的，如果某个样本的特征落在策略组和对照组的特征空间中交叉的重叠区域，那么dropout 概率更高。

7.meta-learner

首先根据观测数据生成基本模型，然后对选择偏差造成的有偏估计进行矫正。代表方法是元学习
1.T-learner:2个模型分别预估
2.S-learner:单模型进行预估
3.X-learner:交叉对照组/策略组
4.U-learner
5.R-learner

2.3.3 先验信息：评估类型

因果效应估计：ATT、CATE、ATE、ITE、HTE
ATE ：Average Treatment Effect、ATT ：Average Treatment Effects on Treated、CATE：Conditional Average Treatment Effect、ITE：Individual Treatment Effect
●ATE：平均处理效应，如AB实验，受处理和未受处理的人群的效果的差的期望。
●ATT：受处理的人群的平均处理效应，受处理的人群通过PSM方法找出和他们一样的人做为替身，看他们的效果的差别。
●CATE：人群中某个subgroup的平均处理效应。
●ITE：个体的因果效应，也可以看成是个体的CATE。

2.3.4 模型选择

Meta learner(S-learner/T-learner/X-learner)、Tree based、深度学习

2.3.5 弹性保序_负弹性

保序在实际应用过程中经常出现，由于观测数据的偏差不同，会出现补贴越多反而转化越低的问题，因此需进行建模保序；半参数学习、DIPN的深度学习

解决负弹性的常用方法：

2.3.6 评估方法

去偏评估、平稳性检查、模型评估：Qini Curve、AUUC、准确程度指标：Bias、MAE、RMSE、因果敏感度分析：安慰实验、添加未观察常识原因。

3.UpLift 模型详解

直接针对潜在结果进行预估时，而不是对观测数据进行matching的过程可以用ml进行因果建模，其中在评估个体增益模型的建模(ITE)时，用到最多的即是uplift，按照个体预估方式可以分为meta、树、深度学习等方式。主要包括meta-learner、tree_base、深度学习，前者可结合ml方法进行分类回归训练，后续主要生产树规则划分整个data在不同的叶子内，而深度学习本质还是s-learner，其中对网络结构做了部分改造。

3.1.meta-learner

3.2.tree_base

解决unobserved confounder的一个情况，因果森林跟随机森林类似，也是由多颗树构成。每棵树都是因果树，预估的是满足叶子结点规则的人群平均处理效应（ATE）。不同的是分裂准则不一样，传统的回归树分裂准则是让数据集平均MSE最小化，因果树分裂准则是让分裂后的两个子集的uplift差异越大越好，这样就能将uplift高的用户和uplift低的用户区分开来，同时也希望保证两个子集的样本数目比较均匀。分裂标准表达式为：

这个表达式中，P代表决策树父节点，C1和C2是分裂后的2个子节点，θ 是两个子集的平均处理效应。因为两个子集中既有T=1的样本，也有T=0的样本，所以可以计算出平均处理效应，即平均增益。n代表各集合的样本数目。决策树分裂要求上述表达式的值最大化。传统的回归树，叶子结点预测结果是叶子结点上样本的响应变量平均值。类似的，因果树预测的结果是，叶子结点上的平均CATE，以发优惠券为例，叶子结点预测的结果就是该节点上发券样本的平均转化率 - 不发券样本的平均转化率。

3.3.深度学习

解决领域偏移问题时，我们就希望能balance数据使得这treatment与control分布尽可能接近。其实这也可以理解为在解决有unobserved confounder的一个情况，因为这就可以理解为我们有一些不可控的变量会同时影响着T和Y，主要使用表征学习思想，其中TARNet与Dragonnet讨论比较多.
1.TARNet/CFR*
2.SITE
3.Perfect Match
4.Dragonnet*
5.CEVAE
6.BNN/BLR

4.连续变量下的因果效应评估

区别于二值的因果建模，连续因果建模有不同的treatment，因此在观测数据中进行连续值评估的场景更加具有泛化性，但评估难度也相对较大。

4.1 连续因果森林

基于二元因果森林的多元处理效应估计

方案一：这样，通过上述的简单改造，我们就可以基于现有的二元处理效应模型，实现多元处理效应的估计。
●优点：易于实现，无需额外开发；所有二元处理效应模型均适用。
●缺点：当处理变量值较多时，会产生大量模型，增加训练和部署成本；数据利用不充分，单个模型只用到部分(2/(k+1))数据；不同处理效应间无关联。这在部分场景中并不合理，例如我们认为价格和供需存在单调关系；无法对未出现在数据集中的对照变量值进行推断。
方案二：基于这个想法，在ATE的基础上，我们定义平均偏效应(Average Partial Effect)为
，上述公式等价于Y对W和做简单线性回归后得到的斜率系数。
通过将CAPE代替CATE作为节点统计值用作树分裂，我们就实现了通过单一模型估计多元/连续处理效应。在模型的预估/推断阶段，为了跳脱出线性假设的约束， 在估计各个对照处理效应的时候，我们退回之前的定义，仅选取对应的对照/参照变量值样本计算对应的处理效应。因此在我们的连续因果森林模型中，整体的CAPE仅被用作分裂，不会用于效应估计。
●优点：考虑了不同处理效应间的关系；充分利用数据，不同处理变量间可以互相学习；单一模型，减少训练/部署成本。
●缺点：使用中需考察线性假设的合理性。

4.2 其他深度学习方法

4.2.1.GPS(generalized propensity score)

propensity score(广义倾向分)在二值时的应用常见包括PSM对应的PSS、IPTW、PSM等，基本原理都是利用P(T=1|X)的概率进行匹配的到weak unconfoundedness的观测数据然后进行评估。
算法描述：假定在X确定下T的分布符合‘正太形式’,通过极大似然估计得到正太的变量ß和å ，后续算出T的平衡分，得到平衡分之后构造2次回归模型，预估回归模型的参数后，得到求解效应的函数;即为一阶段拟合平衡分、二阶段假定多项式拟合因果效应

4.2.2.DML(double machine learning)

DML为双重机器学习，一般分linear和nonLinear两种。
算法描述：首先拟合两个残差，一个是X对应的Y(x对应的label)，另一个是X对应的T(x对应的treatment概率)对应为、,这个方法本质也是做了一个假设，就是通过两个残差模型，把T和Y中与X有关的东西都移除掉，残差和X都是正交的，然后拿干净的残差来拟合treatment effect，这样也是一种满足unconfoundedness的方法，也就是把confounder X的影响都剔除了。

4.2.3.GRF(generalized random forest)*

广义随机森林目前在多个连续因果场景表现较好 ，相对复杂些,应用场景涉及quantile regression(分位点回归), conditional average partial effect estimation(期望回归) and heterogeneous treatment effect estimation（因果效应推断）。
算法描述：一阶段拟合DML类似的双残差，第二阶段使用CART树进行因果效应拟合。
算法细节：因果效应估计中构建树时，并不使用原始的Y和W，而是类似Double Machine Learning，先训练Y预估和W预估模型，然后对每个样本预估 和 ，使用被中心化后的 , 作为label参与建模和预估。Local centering在非随机数据上尤其有用(减小confounder的影响,二者分别在相减时，去除了混淆的隐变量影响)。GRF本质是随机森林，需要独立建多棵树，主要构造CART树、下面以分裂节点准则、评估方法进行展开。
首先定义目标的损失函数为O,这是带有å权重的损失函数。其中的权重参数定义为训练样本和他的相似度是看在随机森林里他们俩在同一个叶子节点的次数多不多，越多越像，越像最后算损失的时候权重越大。

5.结果评估

5.1 增益评估指标

衡量ITE指标的常用有AUUC、Qini

5.2 其他评估指标

数据去偏、ATE结果衡量用于筛选高增量用户群体等

6.因果推断拓展

6.1 Lookalike

lookalike 的目的是基于目标人群，从海量的人群中找出和目标人群相似的其他人群，这也是受众定向技术之一。Lookalike，即相似人群扩展，是基于种子用户，通过一定的算法评估模型，找到更多拥有潜在关联性的相似人群的技术。值得注意是，Lookalike不是某一种特定的算法，而是一类方法的统称，这类方法综合运用多种技术，比如协同过滤、node2vec等，最终达到用户拓展目的。
●基于社交关系的扩散：以具有相似社交关系的人也有相似的兴趣爱好/价值观为前提假设，利用社交网络关系进行人群扩散，一般平台会通过登录QQ、手机通讯权限或者其他社交媒体粉丝、古关注等信息进行种子人群的扩散。
●人工选择标签扩散：DMP的人群圈选一般是多个标签的组合人群，如果希望去做相似人群的，可以对存量的人群进行画像的解析，然后再对标签泛化找到机会人群。
●基于标签的协同过滤：在标签扩散的基础上，采用基于User-CF协同过滤算法，找到与种子人群相似的机会人群，例如在电商平台中，有点击、加购以及入会收藏多个相似商品之间的用户，计算相似余弦距离，再进行加权平均，详情可见Arthur关于推荐系统召回的文章。
●基于K-Means 聚类的扩散：根据用户画像或标签，采用层次聚类算法（如BIRCH或CURE算法）对人群进行聚类，通过画像、标签内容去找到聚类相似性，再过制定相似的阈值从中找出与种子人群相似的机会人群。
●基于向量相似度embedding方法：把用户user embedding，映射到对应的低维度向量当中，再根据k-means做局部敏感的hash聚类，根据用户属于哪个聚类再进行对应的推荐
●目标人群分类方法：以种子人群为正样本，候选对象为负样本，训练分类模型，然后用模型对所有候选对象进行筛选，涉及PU Learning的问题。
e.g.: 微信看一看的RALM示例：最下层的离线训练、到在线异步处理，再到在线服务

6.2 pulearning

因果推断场景中，会存在单样本存量较多的情况，此时需借助pulearning进行负样本学习，达到数据泛化的作用。

6.3 小样本学习

小样本学习、元学习、迁移学习等，在模型研究中讨论较多，其中小样本学习作为业界解决样本缺失问题的有效方式，在日常建模中也经常使用。从主动学习、数据增强、半监督学习、领域迁移、集成学习&自训练几个方向介绍了现有的一些方法。由于因果场景的历史投放方案变动过小，模型依靠历史数据训练，泛化性指标和精度无法满足业务要求，因此需要找到合适的样本收集机制，满足以下两个目标：
●·收集的样本是正式投放中较为类似的样本，提高样本的可利用效率, 为模型提供更多信息。
●·收集的样本具备较好的业务指标，满足业务指标要求。
主要方法
通过启发式算法(模拟退火、蚁群…)在较大的方案空间内搜寻全局最优解，主要使用进化算法。通过模型的预估结果调整进化方向，在模型精度较好时，提高线上业务效果；精度较差时，收集到了模型高价值的样本。
●召回方案生成初始父代
●进化策略进化新的子代
●选择模型预估最优方案
应用流程：
●初始化
●进化
●选择
●重复进化和选择直到达到收敛。
●模型使用进化策略得到的样本进行fine tune，实现离线指标优化，新模型指导进化策略方向的优化。

6.4 PID

pid(Process Identifier)作为线上实时预算调整分配环节，在实际应用中往往存在补贴进度与实际预估进度不符的情况，因此需要结合pid进行实时调整。

6.5 因果图介绍

以上讲解的多数为潜在因果模型，因果图挖掘(SCM)作为因果推断领域的另一种方法，在实际应用中也有较多经典算法，因果图框架主要分为两个问题，构建图、基于图的因果推理，其中构建图指在高纬变量空间内找到变量之间的量量条件关系，组成因果图，基于图的因果推理，假定图以及产生的情况下基于完备的后门准则、do运算这类理论可以很好的进行因果推理、因果发现，根据上述两类问题进行介绍。
●因果图构建
从变量空间内找到两两之间的相互关系，进而构建出因果图框架
●基于因果图的推理
d分离，do运算，前门准则和后门准则

6.6 非满足假设条件算法

6.6.1 工具变量(IV)

在实际中做因果分析时，我们往往无法判断是否完全掌握了对结果产生需要的所有信息，尤其有一些混淆变量（confounders）即使知道它的存在，也可能是无法度量或无法采集到信息的。
比如，当我们考察教育程度对收入的影响时， 教育程度或高或低的人群是不一样的，其中“个人能力”的差异是难以度量的，但却会同时影响教育程度和收入；
比如，当我们考察抽烟对健康的影响时，抽烟或不抽烟的人群是不一样的，其中“生活习惯”的差异是难以度量，同时影响着是否抽烟以及健康。
在以往讨论的因果推断/uplift 建模方法时，我们都提到了一个“可忽略性假设” ：unconfoundedness、Ignorability
既然我们关心的因变量（treatment）会受到隐藏的混淆因素影响，那么，是否可以找一个不受隐藏的混淆因素干扰的工具变量间接预估因果效应呢？ 这就是工具变量法（Instrumental Variables）的解决思路。
●工具变量（IV）需要满足 两个条件： 1）与treatment相关，确保是有效的工具变量；2）只能通过影响 treatment来 影响outcome。
●记住，我们始终都只是在间接地估计ATE
●工具变量（IV） 不是什么灵丹妙药，不是万能的。 甚至当 the first stage 很弱时，还会带来麻烦。事实上，工具变量法最大的问题是满足研究条件的工具变量难以找到，而不合乎条件的工具变量只能带来更严重的估计问题

6.6.2 后门调整

●后门标准（后门准则）：如果变量集Z满足：① 不包含X的子孙节点；② 阻断了X到Y的所有后门路径。则称Z满足(X, Y)的后门准则
●后门调整：基于后门路径，通过干预do算子消除混淆因子的影响，仅使用已知的数据分布，估计变量之间的因果效应

一开始的辛普森悖论，可以通过切断症状的影响进行评估，实际运算上把症状的百分比带进去即可

6.7 帕累托最优

区别于零和博弈，帕累托最优（Pareto Optimality），也称为帕累托效率（Pareto efficiency），是指资源分配的一种理想状态，假定固有的一群人和可分配的资源，从一种分配状态到另一种状态的变化中，在没有使任何人境况变坏的前提下，使得至少一个人变得更好，这就是帕累托改进或帕累托最优化。
实际营销场景中我们经常会考虑资源最大化的情况，实际操作的问题转化为0-1背包，动态规划等方案，帕累托最优的改进和优化方法可以作为final target，作为衡量全局最优的一个参考依据。
后续
1.适配营销场景，在业务规则，总包等限制下的ROI最大化
2.因果关系下的变量筛选，得到不同因果变量之前的关系，用于特征筛选等
3.大模型结合下的因果推断有哪些应用场景?
4.因果场景经常存在的问题

附录

附一：因果关系梳理览图

附二：基于假设下的算法分类图

附三：建议应用学习路线

因果推断的涉及范围较广，实际的工业应用上的学习思路可以参考：
●uplift model(meta learning、因果森林)—>psm/iptw/ipw—>auuc/qini—>did/断点回归—>grf/dml—>iv—>… … …

附四: 开源的技术框架及大脑的算法文件引用

●开源技术框架：