关于学习的定义
学习是指通过训练使个体在行为上产生较为持久改变的过程,一般来说效果随着训练的增加而提高,即通过学习获得进步。
人工神经网络的功能由其连接的拓扑结构和网络的连接权值决定,其全体的权值 W 整体反映了神经网络对于所解决问题的知识存储。即一旦拓扑结构和权值确定,该网络就可以应用于新的数据得到结果。
人工神经网络的学习就是通过对样本的学习训练,不断改变网络的拓扑结构及连接权值,使得输出不断的接近期望输出值。
通过训练改变权值的规则被称为学习算法或者学习规则,有时也称作训练规则或者训练算法,学习规则对人工神经网络非常重要。
学习规则的类型
按照一般的分类标准通常分为三类:
- 有监督学习:学习模式为纠错
不断的给网络提供一个输入,即其期望的正确输出(称教师信号),将ANN的实际输出和期望输出作比较,不符时,按照一定规则调整权值参数,重新计算、比较,直到网络对于给定的输入均能产生期望的输出,则认为该网络训练完成,即已学会样本数据中的知识和规则。即可用于解决实际问题。 - 无监督学习:学习模式为自组织
学习时不管给网络提供动态输入信息,网络根据特有的内部结构和学习规则,在输入信息流中发现可能的模式和规律,同时根据网络功能和输入信息调整权值(自组织)。使网络能对属于同一类的模式进行自动分类。该模式网络权值的调整不取决于教师信号,网络的学习评价标准隐含于网络内部。 - 灌输式学习:学习模式为死记硬背
将网络设计成记忆特别的例子,当输入为该例子时,网络可以回忆起该例子。网络权值非训练得到,而是通过某种设计方法得到,权值一旦设计好,即一次性灌输给网络,不再变动。
赫布法则
唐纳德·赫布(Donald Olding Hebb)在《The Organization of Behavior》书中解释了学习过程中大脑中的神经细胞是如何改变和调整的,他认为知识和学习发生在大脑,主要是通过神经元间突触的形成与变化。当细胞A的轴突足以接近以激发细胞B,并反复持续地对细胞B放电,一些生长过程或代谢变化将发生在某一个或这两个细胞内,以致A作为对B放电的细胞中的一个效率增加。
通俗来讲就是两个神经细胞交流越多,它们连接的效率就越高,反之就越低。
M-P模型缺乏一个对人工智能而言至关重要的学习机制,M-P模型很好的简化、模拟了神经元,但是无法通过学习的方式调整、优化权重,形成有效的模型。赫布法则的出现,成为神经模型的训练(学习机制)的基础性工作。
赫布规则通常用作无监督神经网络的学习,常应用于自组织神经网络、竞争网络中。
赫布学习规则
赫布学习规则为前馈、无导师学习。只根据实际输入和输出调整权重。
在赫布学习规则中,学习信号简单的等于神经元的输出:
r
=
f
(
W
j
T
X
)
r=f(W_j^TX)
r=f(WjTX)
权值向量的调整公式为:
△
W
j
=
η
f
(
W
j
T
X
)
X
,
η
为
常
数
△W_j=ηf(W_j^TX)X,η为常数
△Wj=ηf(WjTX)X,η为常数
权向量各个分量调整为:
△
w
i
j
=
η
f
(
W
j
T
X
)
x
i
=
η
o
j
x
i
,
i
=
0
,
1
,
.
.
.
,
n
△w_{ij}=ηf(W_j^TX)x_i=ηo_jx_i,i=0,1,...,n
△wij=ηf(WjTX)xi=ηojxi,i=0,1,...,n
赫布学习规则的步骤:
- 初始化权值参数W,一般赋于0附近的随机数
- 初始化学习率η
- 对所有输入记录:
- 根据输入记录,更新权重值
例:设阈值为
T
=
0
T=0
T=0,学习速率
η
=
1
η=1
η=1,初始权值
W
(
0
)
=
(
1
,
−
1
,
0
,
0.5
)
T
W^{(0)}=(1,-1,0,0.5)^T
W(0)=(1,−1,0,0.5)T,输入样本有
X
(
1
)
=
(
1
,
−
2
,
1.5
,
0
)
T
,
X
(
2
)
=
(
1
,
−
0.5
,
−
2
,
−
1.5
)
T
,
X
(
3
)
=
(
0
,
1
,
−
1
,
1.5
)
T
X^{(1)}=(1,-2,1.5,0)^T,X^{(2)}=(1,-0.5,-2,-1.5)^T,X^{(3)}=(0,1,-1,1.5)^T
X(1)=(1,−2,1.5,0)T,X(2)=(1,−0.5,−2,−1.5)T,X(3)=(0,1,−1,1.5)T,激活函数
f
(
x
)
=
s
g
n
(
x
)
f(x)=sgn(x)
f(x)=sgn(x),使用赫布规则训练网络
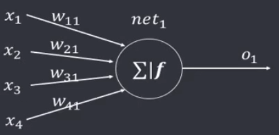
代入第一个样本
X
(
1
)
X^{(1)}
X(1),计算
n
e
t
1
(
1
)
net_1^{(1)}
net1(1):
n
e
t
1
(
1
)
=
(
W
(
0
)
)
T
X
(
1
)
=
(
1
−
1
0
0.5
)
(
1
−
2
1.5
0
)
=
3
net^{(1)}_1=(W^{(0)})^TX^{(1)}=\begin{pmatrix}1 & -1 & 0 & 0.5\end{pmatrix}\begin{pmatrix}1\\-2\\1.5\\0\end{pmatrix}=3
net1(1)=(W(0))TX(1)=(1−100.5)⎝⎜⎜⎛1−21.50⎠⎟⎟⎞=3
根据第一个样本
X
(
1
)
X^{(1)}
X(1),更新
W
(
0
)
W^{(0)}
W(0):
W
(
1
)
=
W
(
0
)
+
η
f
(
(
W
1
(
0
)
)
T
X
(
1
)
)
X
(
1
)
=
W
(
0
)
+
η
∗
s
g
n
(
n
e
t
1
(
1
)
)
∗
X
(
1
)
=
(
1
−
1
0
0.5
)
+
1
∗
1
∗
(
1
−
2
1.5
0
)
=
(
2
−
3
1.5
0.5
)
W^{(1)}=W^{(0)}+ηf\Big((W^{(0)}_1)^TX^{(1)}\Big)X^{(1)}\\\quad\quad=W^{(0)}+η*sgn(net^{(1)}_1)*X^{(1)}\\\quad\quad=\begin{pmatrix}1\\-1\\0\\0.5\end{pmatrix}+1*1*\begin{pmatrix}1\\-2\\1.5\\0\end{pmatrix}=\begin{pmatrix}2\\-3\\1.5\\0.5\end{pmatrix}
W(1)=W(0)+ηf((W1(0))TX(1))X(1)=W(0)+η∗sgn(net1(1))∗X(1)=⎝⎜⎜⎛1−100.5⎠⎟⎟⎞+1∗1∗⎝⎜⎜⎛1−21.50⎠⎟⎟⎞=⎝⎜⎜⎛2−31.50.5⎠⎟⎟⎞
代入第二个样本
X
(
2
)
X^{(2)}
X(2),计算
n
e
t
1
(
2
)
net_1^{(2)}
net1(2):
n
e
t
1
(
2
)
=
(
W
(
1
)
)
T
X
(
2
)
=
(
2
−
3
1.5
0.5
)
(
1
−
0.5
−
2
−
1.5
)
=
−
0.25
net_1^{(2)}=(W^{(1)})^TX^{(2)}\\\quad\quad =\begin{pmatrix}2 & -3 & 1.5 & 0.5\end{pmatrix}\begin{pmatrix}1\\-0.5\\-2\\-1.5\end{pmatrix}=-0.25
net1(2)=(W(1))TX(2)=(2−31.50.5)⎝⎜⎜⎛1−0.5−2−1.5⎠⎟⎟⎞=−0.25
根据第二个样本
X
(
2
)
X^{(2)}
X(2),更新
W
(
1
)
W^{(1)}
W(1):
W
(
2
)
=
W
(
1
)
+
η
f
(
W
1
T
X
(
2
)
)
X
(
2
)
=
W
(
1
)
+
η
∗
s
g
n
(
n
e
t
1
(
2
)
)
∗
X
(
2
)
=
(
2
−
3
1.5
0.5
)
+
1
∗
(
−
1
)
∗
(
1
−
0.5
−
2
−
1.5
)
=
(
1
−
2.5
3.5
2
)
W^{(2)}=W^{(1)}+ηf(W^T_1X^{(2)})X^{(2)}\\\quad\quad=W^{(1)}+η*sgn(net^{(2)}_1)*X^{(2)}\\\quad\quad=\begin{pmatrix}2\\-3\\1.5\\0.5\end{pmatrix}+1*(-1)*\begin{pmatrix}1\\-0.5\\-2\\-1.5\end{pmatrix}=\begin{pmatrix}1\\-2.5\\3.5\\2\end{pmatrix}
W(2)=W(1)+ηf(W1TX(2))X(2)=W(1)+η∗sgn(net1(2))∗X(2)=⎝⎜⎜⎛2−31.50.5⎠⎟⎟⎞+1∗(−1)∗⎝⎜⎜⎛1−0.5−2−1.5⎠⎟⎟⎞=⎝⎜⎜⎛1−2.53.52⎠⎟⎟⎞
代入第三个样本
X
(
3
)
X^{(3)}
X(3),计算
n
e
t
1
(
3
)
net_1^{(3)}
net1(3):
n
e
t
1
(
3
)
=
(
W
(
2
)
)
T
X
(
3
)
=
(
1
−
2.5
3.5
2
)
(
0
1
−
1
1.5
)
=
−
3
net_1^{(3)}=(W^{(2)})^TX^{(3)}\\\quad\quad =\begin{pmatrix}1 & -2.5 & 3.5 & 2\end{pmatrix}\begin{pmatrix}0\\1\\-1\\1.5\end{pmatrix}=-3
net1(3)=(W(2))TX(3)=(1−2.53.52)⎝⎜⎜⎛01−11.5⎠⎟⎟⎞=−3
根据第三个样本
X
(
3
)
X^{(3)}
X(3),更新
W
(
2
)
W^{(2)}
W(2):
W
(
3
)
=
W
(
2
)
+
η
f
(
W
2
T
X
(
3
)
)
X
(
3
)
=
W
(
2
)
+
η
∗
s
g
n
(
n
e
t
1
(
3
)
)
∗
X
(
3
)
=
(
1
−
2.5
3.5
2
)
+
1
∗
(
−
1
)
∗
(
0
1
−
1
1.5
)
=
(
1
−
3.5
4.5
0.5
)
W^{(3)}=W^{(2)}+ηf(W^T_2X^{(3)})X^{(3)}\\\quad\quad=W^{(2)}+η*sgn(net^{(3)}_1)*X^{(3)}\\\quad\quad=\begin{pmatrix}1\\-2.5\\3.5\\2\end{pmatrix}+1*(-1)*\begin{pmatrix}0\\1\\-1\\1.5\end{pmatrix}=\begin{pmatrix}1\\-3.5\\4.5\\0.5\end{pmatrix}
W(3)=W(2)+ηf(W2TX(3))X(3)=W(2)+η∗sgn(net1(3))∗X(3)=⎝⎜⎜⎛1−2.53.52⎠⎟⎟⎞+1∗(−1)∗⎝⎜⎜⎛01−11.5⎠⎟⎟⎞=⎝⎜⎜⎛1−3.54.50.5⎠⎟⎟⎞
离散感知器学习规则
感知器(Perceptron)是由Rosenblatt定义的具有单层神经计算单元的神经网络结构。实际上为一种前馈网络,同层内无互连,不同层间无反馈,由下层向上层传递,其输入、输出均为离散值,神经元对输入加权求和后,由阈值函数(激活函数)决定其输出。
离散感知器学习规则则代表一种有导师的学习方式,其规定将神经元期望输出(教师信号)与实际输出之差作为学习信号,通过训练调整权值直到实际输出满足要求(等于或者接近于期望输出)。
在该学习规则中,学习信号等于神经元的期望输出与实际输出之差:
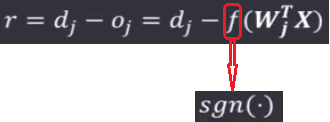
权值调整公式为:
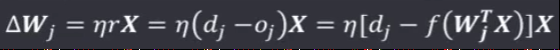
权向量各个分量调整为:

离散感知器学习规则的步骤:
- 初始化权值参数W,学习速率η
- 对每一个样本,实际输出和期望输出的差是否满足要求:
- 根据输入记录,更新权重值
例子:

连续感知器学习规则:δ规则
Delta学习规则(δ Learning Rule):1986年,由认知心理学家McClelland和Rumellhart在神经网络训练中引入了学习规则。一种简单的有导师学习算法,该算法根据神经元的实际输出与期望输出差别来调整连接权。
Delta学习规则的思路如下:系统首先用一个输入向量,输入网络结构,得到一个输出向量;每个输入向量都有一个对应的期望输出向量、或者称作是目标向量;比较实际输出向量与期望输出向量的差别,若没有差别,就不再继续学习;否则,连接的权重修改对应的差值(delta差)。
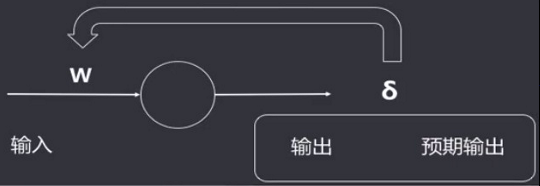
梯度(Gradient):是一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向变化最快,变化率最大。
梯度下降法(GradientDescent):一种最优化算法,也称为最速下降法。沿着负梯度方向去减小函数值从而接近目标值。


确定了损失函数,就需要对损失函数进行优化,求最小值,以平方损失函数(QuadraticLF)为例:
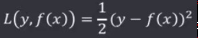
求 L 的梯度:
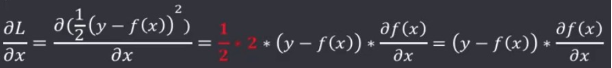
假设激活函数选用了sigmoid函数:
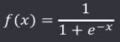
求出此时 L 的梯度:
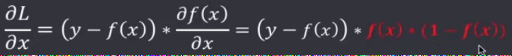
δ规则的学习信号为:
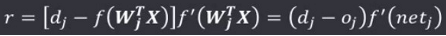
δ规则的推导:由输出值与期望输出值的最小二次方误差条件,推导δ规则
输出值与期望输出值的二次方误差为: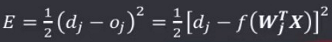
学习的目的就是为了让实际输出值与期望输出值的差最小,即求使 E 最小的权值 W 。根据之前的损失函数和梯度、梯度下降法可以知道,W 沿着梯度的负方向(最小值)按照步长η(学习速率)变化,会快速逼近最小值,即有:
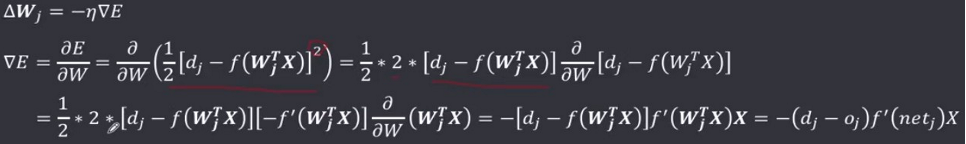
最小均方学习规则
1962年Bernard Widrow和Marcian Hoff提出了Widrow-Hoff学习规则,它可以使神经元实际输出和期望输出之间的二次方的差最小,所以又称为最小均方学习规则(Least-Mean-Square,LMS)。
LMS规则的学习信号为:
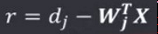
权向量调整量为:
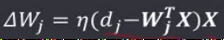
权值分量调整为:
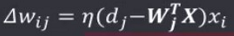
最小均方算法是δ学习规则的特例,其激活数不同于δ学习规则,不做任何变换:
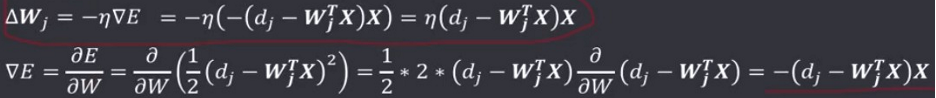
最小均方算法和δ学习规则相比,无需求导数,学习速度快,且有不错的精度
相关学习规则
相关学习规则的学习信号为:

权向量调整量为:
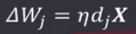
权值分量调整为:

赫布学习规则:
在该学习规则中,学习信号等于神经元的期望输出与实际输出之差:

权值调整公式为:

权向量各个分量调整为:
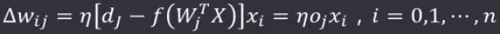
相关学习规则从权值调整上来看,是赫布学习规则的一个特例:当赫布规则的激活函数为二进制函数且有

时,二者一致。
相关学习规则是有导师学习,赫布规则是无导师学习。
竞争学习(Competition Learning):是人工神经网络的一种学习方式,指网络单元群体中所有单元相互竞争对外界刺激模式响应的权利。竞争取胜的单元的连接权重向着对这一刺激有利的方向变化,相对来说竟争取胜的单元抑制了竟争失败单元对刺激模式的响应。属于自适应学习,使网络单元具有选择接受外界刺激模式的特性。竞争学习的更一般形式是不仅允许单个胜者出现,而是允许多个胜者出现,学习发生在胜者集合中各单元的连接权重上。
胜者为王学习规则(Winner-Take-All):无导师学习,将网络的某一层设置为竞争层,对于输入X竟争层的所有p个神经元均有输出响应,响应值最大的神经元在竞争中获胜,即:
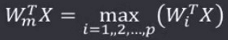
获胜的神经元才有权调整其权向量Wm,调整量为:△Wm=α(X-Wm),α∈(0,1],随着学习而减小在竞争学习过程中,竞争层的各神经元所对应的权向量逐渐调整为输入样本空间的聚类中心。在实际应用中,通常会定义以获胜神经元为中心的邻域,所在邻域内的所有神经元都进行权重调整。
例子:

外星学习规则
内星节点:总是接收其他神经元输入的加权信号,是信号的汇聚点,其对应的权值向量称作内星权向量。
外星节点:总是向其他神经元输出加权信号,是信号的发散点,其对应的权值向量称作外星权向量。
内星学习规则:内星节点的输出响应是输入X和内星权向量W的点积,描述了输入与权向量的相似程度,其更新规则类似于胜者为王:△Wj=α(Xi-Wj)
外星学习规则:属于有导师学习,其目的是为了生成一个期望的m维输出向量d,外星权向量Wj更新通过两者的差异实现,
其规则为:△Wj=η(d-Wj)

两者的更新规则:
内星属于无导师学习,外星属于有导师学习
内星更新依赖于输入和权重的差异,外星更新依赖于输出和权重的差异























 5550
5550











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










