原文链接:https://www.yuque.com/yahei/hey-yahei/objects_detection#zoJwH
损失函数
目标检测中最经典的损失函数就是Faster RCNN所用的“softmax交叉熵分类损失 + SmoothL1回归损失”的形式,后来有很多改进的目标检测网络、方案也陆续提出了一些损失函数上的改进。
分类损失
参考:
- 《目标检测小tricks–样本不均衡处理 | 知乎, 燕小花》
- 《样本贡献不均:Focal Loss和 Gradient Harmonizing Mechanism | 知乎, BeyondTheData》
- 《Imbalance Problems in Object Detection: A Review (IEEE-PAMI2020)》
分类损失的改进主要是解决目标检测中样本不均衡的问题,通常是给难易样本设置一个自适应的权重损失。
Focal Loss
论文:《Focal Loss for Dense Object Detection (ICCV2017)》RetinaNet
作者设计了一个自适应加权的loss,为难样例设置更大的权重,从而提升训练效果。
首先考虑一个二分类的交叉熵(为方便起见,用二分类进行讨论,同理可推广至多分类情况),
C E ( p t ) = − l o g ( p t ) = { − l o g ( p ) , y = 1 − l o g ( 1 − p ) , y = − 1 CE(p_t) = -log(p_t) = \begin{cases} -log(p), & y=1 \\ -log(1-p), & y=-1 \end{cases} CE(pt)=−log(pt)={
−log(p),−log(1−p),y=1y=−1
其中, y ∈ { − 1 , 1 } y \in \{-1, 1\} y∈{
−1,1},而 p p p是预测为 y = 1 y=1 y=1的概率
加入一个人工设置的权重 α \alpha α,缓解样本不均衡的问题,
$$CE’(p_t) = - \alpha_t log(p_t) = \begin{cases}
- \alpha log§, & y=1 \
- (1-\alpha) log(1-p), & y=-1
\end{cases} < b r / > < b r / > 引 入 一 个 自 适 应 的 权 重 , 为 难 样 例 设 置 更 大 的 权 重 , < b r / > <br /> <br />引入一个自适应的权重,为难样例设置更大的权重,<br /> <br/><br/>引入一个自适应的权重,为难样例设置更大的权重,<br/>FL(p_t) = - (1 - p_t)^\gamma \ log(p_t)$$
 - γ \gamma γ是人为设置的超参
- γ \gamma γ越大,难/易样例权重差异就越大
- 当 γ = 0 \gamma = 0 γ=0时,Focal Loss退化为Cross Entropy
- 在论文的实验中, γ = 2 \gamma = 2 γ=2时表现最佳
- 权重 ( 1 − p t ) γ (1-p_t)^\gamma (1−pt)γ会随着正确分类的置信度 p t p_t pt变化
- 当 p t p_t pt比较大时,正确分类的置信度高,属于易样例,权重就比较小
- 当 p t p_t pt比较小时,正确分类的置信度低,属于难样例,权重就比较大
实际操作中,Focal Loss可以结合人工设置的 α \alpha α一起使用,即
F L ( p t ) = − α t ( 1 − p t ) γ l o g ( p t ) FL(p_t) = - \alpha_t \ (1 - p_t)^\gamma \ log(p_t) FL(pt)=−αt (1−pt)γ log(pt)
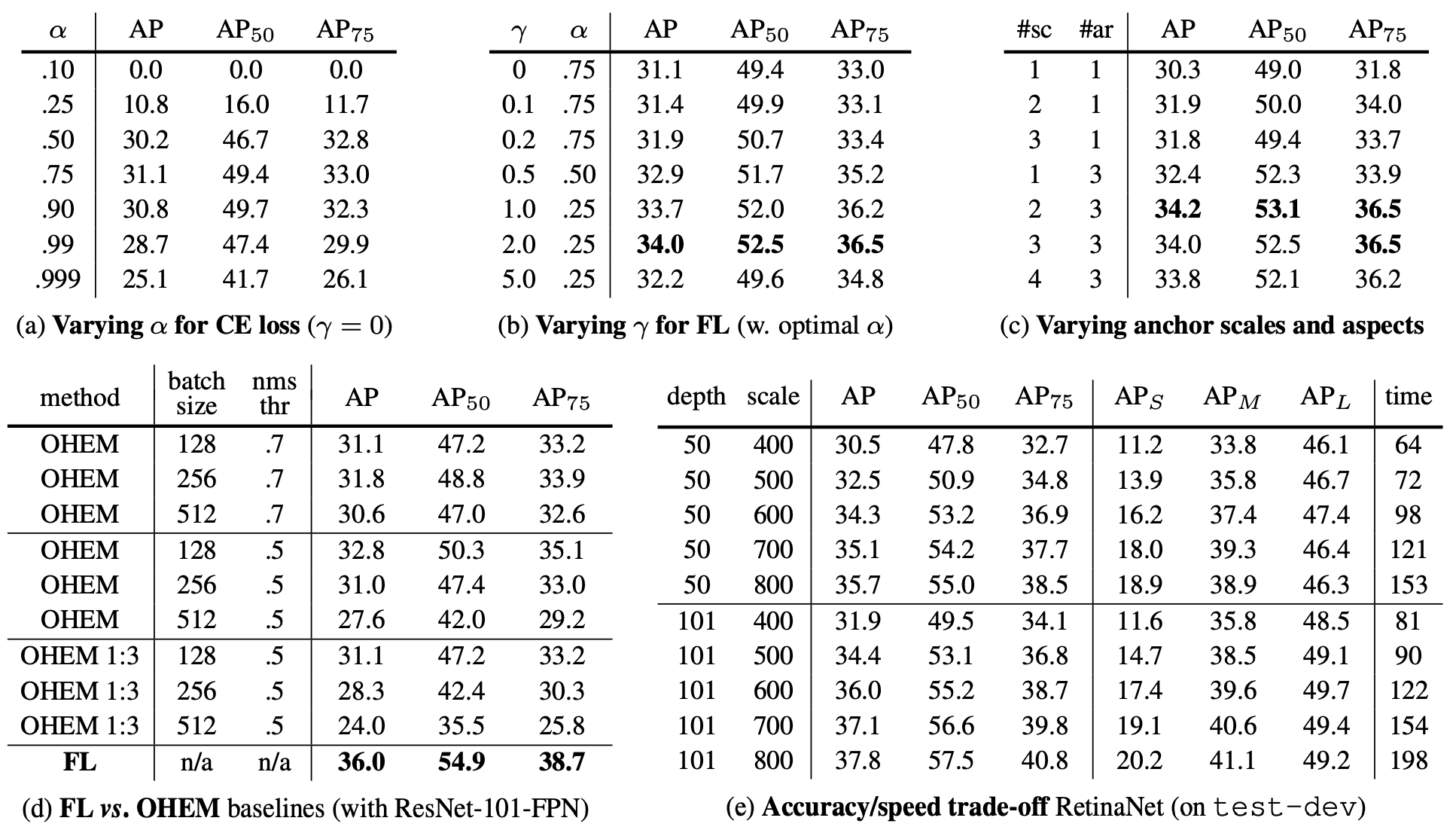
Focal Loss有两个超参 γ \gamma γ和 α \alpha α需要设置,之后一些新的分类损失则进一步简化了形式,提出一些不需要设置额外超参的loss。
Class-Balanced Loss
论文:《Class-Balanced Loss Based on Effective Number of Samples (CVPR2019)》 参考译文
论文提出用样本数量来调节为已有的损失函数加权,以此来缓解样本不均衡问题,应用在Focal Loss上则为
C B focal ( z , y ) = − 1 − β 1 − β n y ∑ i = 1 C ( 1 − p i t ) γ log ( p i t ) \mathrm{CB}_{\text {focal }}(\mathbf{z}, y)=-\frac{1-\beta}{1-\beta^{n_{y}}} \sum_{i=1}^{C}\left(1-p_{i}^{t}\right)^{\gamma} \log \left(p_{i}^{t}\right) CBfocal (z,y)=−1−βny1−βi=1∑C(1−pit)γlog(pit)
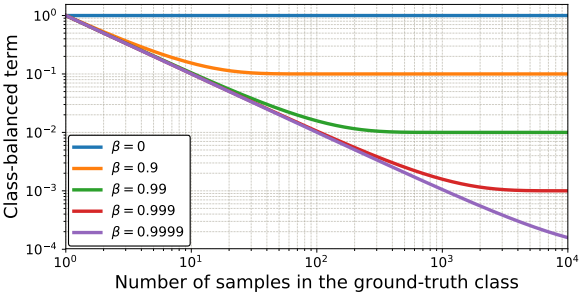
其中,
β ∈ ( 0 , 1 ) \beta \in (0, 1) β∈(0,1)是一个超参;
n y n_y ny是训练集上类别 y y y的样本数;
当 n y n_y ny越大, β n y \beta^{n_y} βny越小,权重 1 − β 1 − β n y \frac{1-\beta}{1-\beta^{n_y}} 1−βny1−β越小,也即样本数量越多,那么他对损失的贡献就越小
AP Loss
论文:《Towards Accurate One-Stage Object Detection With AP-Loss (CVPR2019)》
参考:《感知算法论文(九):Towards Accurate One-Stage Object Detection with AP-Loss | CSDN, 呆呆的猫》
Average Precision Loss(AP Loss)对每个预测框进行排序,用排序后的序号来设计loss,核心思想在于鼓励正样本预测框的得分在负样本得分序列中尽可能靠前。启发自AUC Loss,后者用AUC的排序序号来设计loss,直接对AUC进行优化,而目标检测通常以mAP为指标,因此作者指出直接对AP进行优化能有更好的效果。
Bounding Box的设置方式跟传统的设置方式有些不同。比如有 K K K个分类,
- 传统上是为每个Bounding Box预测一个分类 t i t_i ti( t i ∈ [ 0 , K ] t_i \in [0, K] ti∈[0,K],0表示背景)以及得分向量 ( s i 0 , s i 1 , . . . , s i K ) (s_i^0, s_i^1, ..., s_i^K) (si0,si1,...,siK)
- 论文则是把Bounding Box复制 K K K次,分别用于某一个分类 t i k ∈ { − 1 , 0 , 1 } t_{ik} \in \{-1, 0, 1\} tik∈{ −1,0,1}(-1表示忽略,不纳入AP Loss的计算)的预测,以及得分 s i k s_{ik} sik
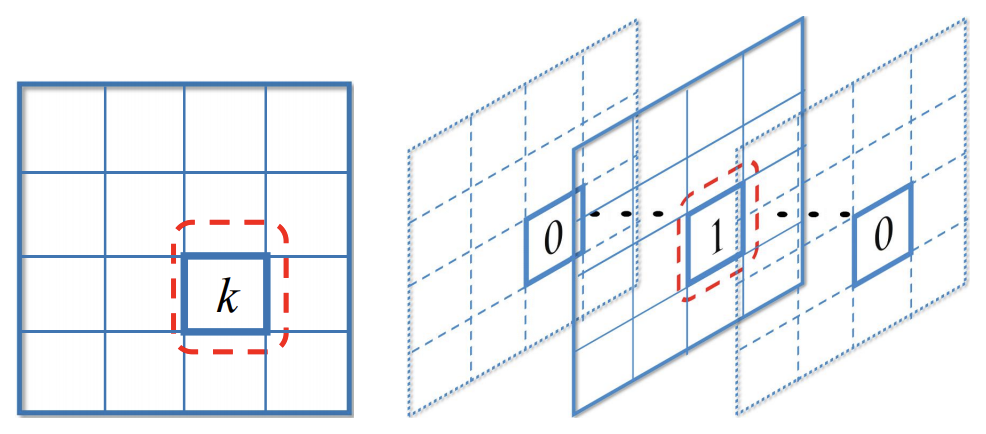
(左:一个label,属于分类k; 右:K个label,第k个为1)
AP Loss的具体设计(与GTBox的IoU超过阈值为正样本,否则为负样本):
- 所有预测框两两之间的得分差值
$$x_{i j}=-\left(s_{i}-s_{j}\right)\$$ - 计算每个预测框的归一化排序(在所有预测框中的排序)
$$L_{ij} = \begin{cases}
0, & s_i > s_j \
\frac{1}{1 + N_{i}}, & s_i \leq s_j
\end{cases}\ < b r / > 其 中 , <br />其中, <br/>其中,N_{i} 是 得 分 大 于 等 于 是得分大于等于 是得分大于等于s_i 的 所 有 预 测 框 数 量 ( 包 括 正 负 样 本 ) ; < b r / > 显 然 , 的所有预测框数量(包括正负样本);<br />显然, 的所有预测框数量(包括正负样本);<br/>显然,L_i = \sum_{j \in P \cup N} L_{ij} 就 是 第 就是第 就是第i 个 预 测 框 在 所 有 预 测 框 中 的 排 序 序 号 , 而 个预测框在所有预测框中的排序序号,而 个预测框在所有预测框中的排序序号,而L_i^{(N)} = \sum_{j \in N} L_{ij} 就 是 第 就是第 就是第i 个 预 测 框 的 得 分 在 所 有 负 样 本 框 中 的 一 个 排 位 ( 归 一 化 的 序 号 , 序 号 越 小 则 得 分 个预测框的得分在所有负样本框中的一个排位(归一化的序号,序号越小则得分 个预测框的得分在所有负样本框中的一个排位(归一化的序号,序号越小则得分s_i 越 高 ) ; < b r / > 也 可 以 展 开 成 关 于 越高);<br />也可以展开成关于 越高);<br/>也可以展开成关于x_{ij} 的 数 学 描 述 , 的数学描述, 的数学描述,L_{i j}=\frac{H\left(x_{i j}\right)}{1+\sum_{k \in \mathcal{P} \cup \mathcal{N}, k \neq i} H\left(x_{i k}\right)}\ < b r / > 其 中 , <br />其中, <br/>其中,H(\cdot) 为 阶 跃 函 数 , 为阶跃函数, 为阶跃函数,H(x)=\left{\begin{array}{ll}
0 & x<0 \
1 & x \geq 0
\end{array}\right.$$ - 计算AP Loss
$$\mathcal{L}{A P}=\frac{1}{|\mathcal{P}|} \sum{i \in \mathcal{P}} \sum_{j \in \mathcal{N}} L_{i j} \ < b r / > 其 中 , <br />其中, <br/>其中,|\mathcal{P}| 是 正 样 本 预 测 框 的 数 量 ; 也 可 以 写 成 , < b r / > 是正样本预测框的数量;也可以写成,<br /> 是正样本预测框的数量;也可以写成,<br/>\mathcal{L}{A P}=\frac{1}{|\mathcal{P}|} \sum{i, j} L_{i j} \cdot y_{i j} = \frac{1}{|\mathcal{P}|} \sum_{i, j} L_{i j}
\cdot \mathbf{1}{t{i}=1, t_{j}=0}\$$ - 显然 L A P \mathcal{L}_{A P} LAP是不可导,所以需要定义近似的更新规则$$\Delta x_{i j}=L_{i j}^{ }-L_{i j} \ < b r / > <br /> <br/>L^{ij} 是 真 实 值 。 < b r / > 当








 本文详细介绍了目标检测中的损失函数,包括分类损失和回归损失。分类损失中,Focal Loss通过为难例加权改善样本不平衡问题,Class-Balanced Loss根据样本数量动态调整权重,AP Loss直接优化平均精度。回归损失方面,GHM-R Loss利用梯度信息对损失进行规范化,IoU Loss、GIoU Loss和DIoU Loss/CIoU Loss则从不同的角度改进了边界框回归的评估标准。
本文详细介绍了目标检测中的损失函数,包括分类损失和回归损失。分类损失中,Focal Loss通过为难例加权改善样本不平衡问题,Class-Balanced Loss根据样本数量动态调整权重,AP Loss直接优化平均精度。回归损失方面,GHM-R Loss利用梯度信息对损失进行规范化,IoU Loss、GIoU Loss和DIoU Loss/CIoU Loss则从不同的角度改进了边界框回归的评估标准。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 776
776

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








