1..经典的K紧邻算法没有加入对分类错误的评估,本文加入了这个模块;相反,以混合分布的概率统计分类方法会提供一个对分类错误的评估,因此本文提出了基于贝叶斯的k紧邻算法来解决这一缺陷。在这之前,Holmes and Adams提出了其他的模型似然函数的分析,特别是k值的选择,我们采用贝叶斯的方法,相比先前Holmes and Adams的研究,本文方法有两个主要贡献点:(1)我们定义了一个封装k紧邻模型的全局概率模型,而不是使用不兼容的条件概率分布;(2)
第二,我们推导出一种适用于我们模型的完全可操作的模拟技术,其基于完美采样或吉布斯采样近似,允许重新评估在这些设置中经常使用的伪似然近似。
1.2 原始K紧邻方法
针对一个二分类的数据集进行交叉验证实验,改变k值得到随着K值变化,引起误分类的错误率变化统计。
针对平均k时,取得的平均错误率,从这个点上引入贝叶斯的观点。
1.3 目标和计划
为了对k紧邻方法进行改进,加入不确定性这个特征,这里加入了一个将标签yi与xi和xi邻居的标签建立一种联系的概率型架构。在原始KNN方法中引入这个想法有两个好处:1.该方法相比与原始的评估方法,在特征向量分类方法增加了更多的信息;(2)它依据贝叶斯推断的引入衡量邻居影响的参数,同时去分析变量的角色、度量、邻居k的数量、类别的数量等一些列因素,从而有助于提高效率。相对来说,这种方法已被提出,我们对已提出的这个联合概率模型进行修改,同时对计算模型评估提供了新的方法。
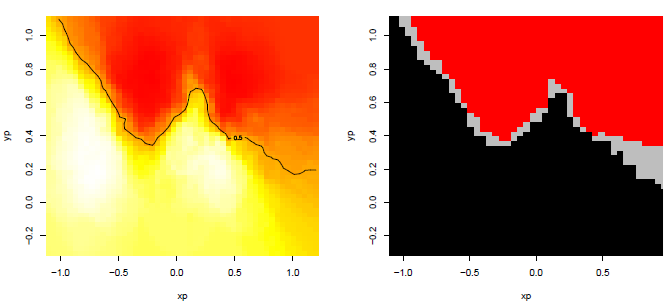
图 1 左图为针对黑色类别的概率评估,计算95%置信区间内这三类的预测概率,检查边界线的概率为0.5,满足这些概率的点被划分为不确定的区域;
本篇文章的整理组织为:首先建立了有效的新的概率型KNN模型,同时指出相Holmes and Adams等方法的不足;接下来讨论了特别针对推断关于k和附加参数所必需的概率k最近邻模型的归一化常数的具体问题。我们利用第3.4节中提出的精确MCMC方法来评估第3.5节中伪似然替代的限制,并说明第4节中几个基准数据集的方法。
2.概率型KNN模型的介绍
2.1马尔科夫随机场模拟
一般为了建立一个能够克隆KNN模型特征的概率性结构然后去评估未知参数,首先定义以xi为条件的标签yi的联合分布,一般来说可以使用这个问题的空间结构约束,然后采用马尔科夫随机场去解决;
虽然我们将在下面显示这在一个连贯的概率设置中是不可能的;然而在这里定义紧邻的联合概率是不可能的,因此需要假设完全条件概率分布
,这里xi仅仅依赖于它的k个邻居;一般来说,
这种条件分布的参数化结构显然是开放的,但是我们选用类似Potts模型或者玻尔兹曼分布等;这种更标准的分布有自身定义的函数:
关于解释见英文部分;
正如在文章Holmes and Adams给出的,其中给出了全概率公式如下所示:
其中β>0,X是训练集(p,n)矩阵{x1,...xn};β衡量不确定的程度,β=0表示所有类一致分布且邻居间相互独立;当β=∞,表示所有邻居极具相关性。尺度参数k使得β在这里无量纲。
上述公式1遇到一个问题是:
译文:即绝大多数数据集在y={y1,...,yn}在满足条件公式1的情况下,不存在一个联合概率分布;
其中解决这个问题的其中方法,可以引用Holmes and Adams中的方法改进了该公式1,定义了直接的联合分布为式2所示:
然而公式2也遇到两个棘手的问题;
因为第一,功能(2)没有正确归一化(Holmes和Adams,2002所忽视的一个事实),必要的规范化常数是难处理的。第二,对应于该联合分布的完全条件分布不由(1)给出。
针对第一个问题,一般在玻尔兹曼机模型也常遇到,解决方案见第3节;一般这类问题的标准的解决方法为使用为似然函数(这在文献Besag 和 Heikkinen),然而这种解决方法只能得到较poor的结果;
第二个更具体的缺点意味着(2)不能被视为伪似然(Besag,1974; Besag et al。,1991 ),因为如上所述,条件分布(1)不能与任何联合分布相关联。从(n = 2,y =(y1; y2)和G = 2的特殊情况可以看出(2)错过归一化常数, 同时公式2丢失了一个固定的常量,关于这个缺点,可以从特定的例子来说明,
从这个公式可以看出,它和1明显不同,更重要的是它严重依赖于参数β和k。
从以上的分析可以看出,针对定义联合分布和条件概率分布遇到一些列问题。
2.2 一个对称的玻尔兹曼模型
鉴于这些困难,因此我们采取不同的策略,并在训练集上定义联合模型:
其中Z(β,k)是分布的归一化常数。这种建模的动机是,可以获得对应于(3)的完全条件分布:
该模型的优势和特点如英文部分介绍;
当邻居系统完全对称(达到因子2)时,原始完全条件(1)完全被(4)替代。
其中,归一化常数Z(β,k)是仍然是棘手的,除了最微不足道的情况。
针对不平衡采样的例子,该k最近邻模型的自然修改是通过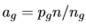
2.3 预测视角
基于条件公式4,对于一个未知数据Xn+1的预测公式表达为下式所示:
其中第一个代表在Xn+1的k个邻居中属于类别g的数量,第二个为将Xn+1当做k个邻居之一的训练样本中的样本观察个数;
此时的模型虽然提供了KNN模型概率的基础,并且也能评估未分类数据的不确定度,然而当多个分类被评估时,它缺乏概率上的一致性。
提出模型遇到的问题,并且同时给出了解决的方案。
在以下部分中,我们主要考察了福尔摩斯和亚当斯(2003)中的情况G = 2,因为这是唯一可以在不同的近似方案之间进行全面比较的情况,但是我们在第3.4节的末尾指出如何 Gibbs采样近似允许对G的较大值的实际扩展,如第4节所示。
3.贝叶斯推断和归一化问题
(这里主要解决如何针对二类问题,采用贝叶斯推断解决未分类点的分类的类别预测问题,即采用贝叶斯的观点,对未知数据做出概率上预测)
从前面的叙述可知,从贝叶斯的观点,未分类点的分类可以基于通过参数的条件后验分布进行积分获得的yn+1的边际预测(或后验)分布,即对于g=1,2,具体采用下式实现:
同时,这里对k和β都有一定的限制。此时对k和β的选择做了分析。
在玻尔兹曼模型中,由于存在相变现象,当β高于某个特定值时,模型可能变成黑白两类(yi = 1,2);
3.1 MCMC步骤
如果后验分布π(β,k|y; X)可用(达到归一化常数),我们可以设计一种MCMC算法,其将产生从该后验近似样本的马尔可夫链(Robert和Casella,2004),例如通过基于k和β的完全条件分布的吉布斯抽样方案。
不能采用基于K和β完全条件分布的吉布斯采样方法模拟的原因,因此采用蒙特卡洛-Hastings的方法进行替换去精确地模拟π(β,k|y; X);
吉布斯取样的替代方法是使用随机游走Metropolis {Hastings算法:然后使用随机游走建议更新β和k。 由于β2(0;βmax)受到约束,我们首先引入β的对数重新参数化,
此时对于β的求解,在
上提出正态随机游走求解更新theta。对于k的求解
为了求解k,这里引入2r邻域内的一致的分布,对于有概率密度Q的分布依赖于参数r,此时需要对其以接受率进行重新标定,在蒙特卡洛-Hastings算法上定义的接受概率为:
这里的步骤主要是完成对(β,k)进行更新求解模拟采样得到其采样数据;
一旦蒙特卡洛方法产生一个(β,k)的满意的序列,对于Xn+1的类别Yn+1就可用公式6进行预测;
这里提出贝叶斯预测的结果其实也是公式6得到概率最大的类别预测,感觉在说明贝叶斯的优势;同时在这里提出针对公式6显示地计算是不可能的,因此这个分布必须采用MCMC链近似模拟,正如公式7表达的那样;然而由于公式3中存在很难求解的常数Z(β,k),以上的框架也不能顺利进行,我们需要用一个易于管理的目标替换掉f。
以下提出3中不同的方法来对待这个难处理的问题:
3.2 伪似然近似
第一个解决方案是采用伪似然来代替真的联合分布,如公式8所示:
并由与(3)相关的(真)条件分布的乘积组成。 然后用真正的后验分布π(β; k|y; X)被下式代替
并在上述草拟的MCMC算法的所有步骤中使用。 基于由此产生的伪样本,来预测分布(yn + 1 = g|xn + 1; y; X)与由(7)产生预测结果的比较近似。
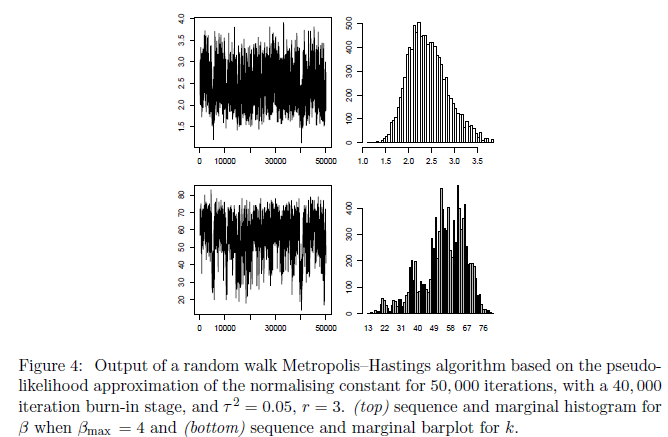
对图4的结果说明:
如图4所示,对于Ripley的基准数据,随机漫步蒙特卡洛-Hastings算法以上详细描述,尽管混合很慢(左下图可说明),但伪像似然近似也令人满意。 在该数据集上,对于k ^ = 53和β^ = 2:28,实现了伪最大值(即最大值(8))。 如果我们使用最后该MCMC运行的1000次迭代,(7)的预测性能使得测试集上的误差率为1000个点中为8.7%。 图4还显示了信息对k的限制。 (注意,我们通过试错来确定βmax= 4的值)。
3.3 路径采样
估计归一化常数的现在标准方法是路径采样,其中两个归一化常数Z(β0;k)=Z(β;k)可以由蒙特卡罗技术近似地被分解为一个积分形式。
路径采样的基本的公式推导;
然而它有一个缺点,就是每步都要计算新的这个归一化常数的比值;
因此,需要采用进一步的路径采样步骤:对于k的每个值和β的几个选定值,我们仅对函数Z(β;k)进行近似,后来我们使用数值插值将函数扩展到β的其他值。由于函数Z(β;k)非常平滑,附加逼近程度相当有限。假定这个近似值只能被计算一次,所得到的蒙特卡洛-hastings算法是非常快的,以及如果通过检查β从一个值到下一个值时Z(β;k)的斜率足够平滑的近似值,(我们强调,由于在(β; k)中的联合近似,产生这些近似所需的计算成本相当高)
我们用Ripley的基准数据集来说明这个近似。 图5给出了对于β的值的范围和k的两个值的近似期望Eβ;k[S(y)]。在期望中,使用系统扫描Gibbs采样器模拟y,因为当仅需要计算一个期望时,使用第3.4节中详细阐述的完美采样方案就没有意义。从该比较图可以看出,当β小时,吉布斯取样器具有良好的混合性能,而对于较大的值,它难以收敛,如在k = 125时右图所示的不良拟合。 在这种情况下,该模型越来越接近相变边界。
图5:对于Ripley基准的期望Eβ;k[S(y)]近似,其中β在0和βmax= 4之间变化,并且对于k = 1(左)和k = 125(右)(104) 对于(β;k)的每个值,进行500次步骤的迭代。 在这些图上,黑色曲线基于期望的线性插值和二阶样条插值的红色曲线。
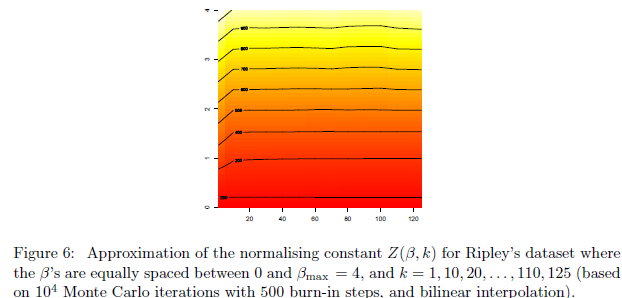
对于Z(β,k)的近似,基于现有的先验知识,我们能够用上式表示log(Z(β,k));并使用数值积分近似这个积分。如图6所示,其使用基于50×12网格的(β; k)值的双线性插值,近似常数Z(β;k)在k中主要是常数。
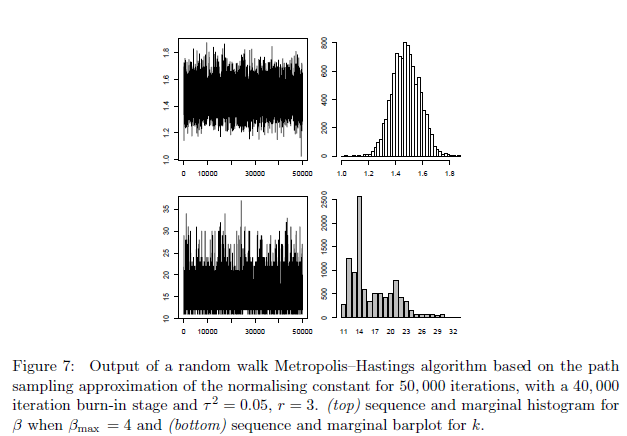
一旦Z(β;k)被近似,我们可以很容易地使用3.1节的真正的MCMC算法,因此这种方法的主要成本在Z(β;k)的近似值中。 图7说明了Ripley基准测试的MCMC采样器的输出,与图4进行比较。第一个令人感兴趣的是,该链混合比其伪似然的方法更快(迭代)。 一个更重要的一点是,两个边际后验分布的近似的范围和形状在两个方法之间差别很大,这是第3.5节中讨论的一个特征。 当(7)中将MCMC采样器的输出用于预测时,Ripley测试集的误码率等于8.5%。
3.4 完美的采样实现和Gibbs近似
这种方案其实在于通过引入辅助变量z来简化模型的求解问题;从后验模拟(β,k,z)等价于从原始数据模拟(β,k),此时,如果我们在这个增强的框架上运行蒙特卡洛-Hastings算法,
这个完美取样器的唯一困难是相变现象,这意味着,对于非常大的β值,过去采样器的耦合的收敛性能相当快地恶化,Møller等人也注意到这一点。(2006)为伊辛模型。我们通过使用基于更小的β值的额外的接受拒绝步骤来克服这个困难,以避免在计算时间内的这种爆炸。
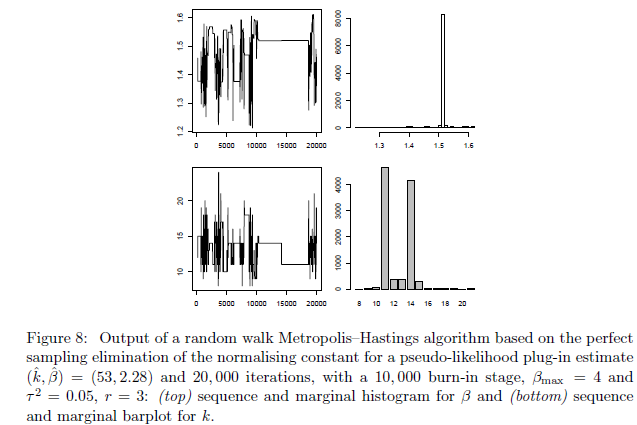
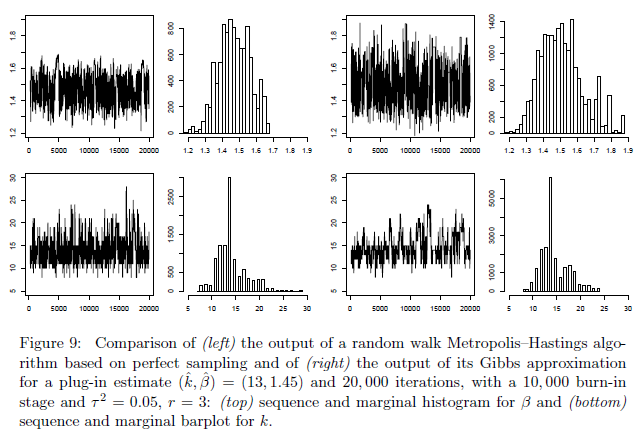
如图8所示,对于(β;k)的不良选择导致算法非常不令人满意的性能。从伪似然估计开始,并使用这个非常值的插件值(β;k),我们获得具有非常低能量和非常高的拒绝率的马尔可夫链。 然而,使用由这种糟糕的运行导致的估计(k;β)=(13; 1.45)确实会大大改善算法的性能,如图9所示。在此设置中,预测误码率 测试数据集等于0.084。
虽然基于辅助变量的优雅解决方案完全消除了归一化常数的问题,但它面临着几个计算困难。首先,如上所述,人造目标g(z|β; k;y)的选择正在推动算法,插值估计需要重新评估周期性。第二,从分布f(z|β;k)的完美模拟是非常昂贵的,如果β接近相转移边界,则可能失败。 此外,该临界点的数值不是预先知道的。 最后,将完美抽样方案扩展到G=2级以上尚未实现。
完美采样和Gibbs采样的对比:
我们提倡用Gibbs取样器代替上述完美的采样器,以实现可管理的计算性能。如果我们用z上的相应的通用Gibbs采样器的500次(完全)迭代代替完美的采样步骤,则计算时间在观测值n中是线性的,而结果和完美采样几乎相同。人们必须记住,对于模拟(β; k)的后验分布的原始问题,z的模拟是二阶的,因为z是引入的辅助变量来克服归一化常数的计算。因此,使用吉布斯取样器引起的额外的不确定性并不严重。图9比较了吉布斯解决方案与完美的采样实施方案,并且显示了使用较便宜的吉布斯采样器造成的损失小,而计算时间的增加则是巨大的。对于50000迭代运行吉布斯采样器所需的时间大约为20分钟,而相应的完美取样器(在相同机器)超过一周。
3.5 伪似然近似估计
鉴于上述替代方案都可以实现为n的小值,因此比较它们以便评估伪似然近似的影响是有直接感兴趣的。如上一节所述,使用Ripley的基准测试训练集达到250点,我们确实能够在可能的β范围内运行一个完美的采样器,这个实现给出了一个采样器,其中唯一的近似是由于运行 MCMC采样器(所有三个版本共同的功能)。
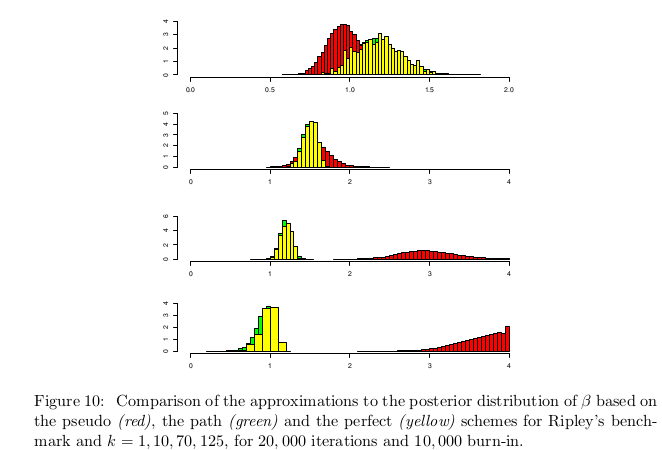
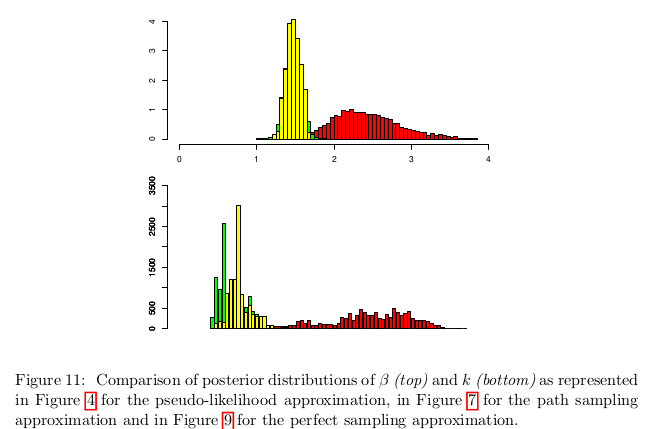
对于相同的数据集,直方图对模拟的β,有条件的或无条件的,在k上显示由伪似然近似产生的样本的总体虚假表示; 参见图10和11.(通过将k设置为固定值,并且运行相应的MCMC算法,直接获得k的固定值的比较。)当然可以认为缺点在于路径对这个常数进行抽样评估,但是这种方法与完美的抽样实施强烈一致,如图所示。因此,在使用伪似然近似时存在根本的差异; 换句话说,伪似然近似定义了(β; k)上明显不同的后验分布。
如图10所示,较大的k是更差的是这种差异,而图11示出了β和k两者都被伪似然近似值显着地高估了。(当我们认识到似然度主要取决于β= k时,很明显地发现β和k之间的这种相关性)。我们还可以注意到,在k的情况下,路径和完美近似之间的对应关系不是绝对的差异可能归因于一个或两个采样器的收敛速度较慢。
为了评估两种方法的比较预测性质,我们还提供了在测试样本的每个点估计的类概率P(y = 1jx; y; X)的比较。如图12所示,预测在范围中间的值是完全不同的,在使用伪似然作为近似值时没有明确的偏向方向。请注意,差异可能很大,可能导致大量不同的分类。
4 在真实数据集上进行验证
本节,对于已提出的各种方法在一些数据集上进行验证测试;
首先,我们使用统一数据集对算法作了校准,作为Møller方案中Gibbs近似的起始值,我们使用最大伪随机估计。 吉布斯采样器被迭代500次,作为完美采样步骤的近似值。 在10000次迭代之后,我们使用当前平均值修改插件估计,然后我们再运行50000次迭代算法。第一个数据集是从R的MASS图书馆借来的。它包括由美国国家糖尿病研究所和消化和肾脏疾病糖尿病测试的532名印度妇女的记录。记录由七个定量协变量组成,标签为是否存在糖尿病。数据随机分为训练集200名女性,其中68名患有糖尿病,测试集332名女性,其中109名患有糖尿病患者。在表2中给出了测试数据集上k的各种值的性能。如果我们使用标准留一去余的交叉验证来选择k(仅使用训练数据集),则连续10个连续的k(即范围57-66)导致相同的错误率。
表2:Pima印度测试数据集上k个最近邻方法的性能
结果在图13中提供。请注意,k的模拟值倾向于避免交叉验证过程发现的区域。这种差异的一个可能原因是,如第2.2节所述,我们的联合模型的似然函数并不直接等同于k最近邻模型的目标函数,因为在这种可能性中相互邻域的邻居的权重相当于单个邻居的两倍。在最后20000次迭代中,预测误差为0.209,与表2中的k最近邻解决方案完全一致。
作者在多个类的数据上进行验证本文提出的算法,为了说明我们的方法考虑两个以上类别标签数据的能力,我们还使用了Ripley(1994)研究的基准数据集法庭玻璃碎片。该数据集涉及九个协变量和六个类,其中一些相当罕据Ripley(1994)的建议,我们合并了一些课程,将课程数减少到四个。 然后我们随机分组数据集,获得训练数据集中的89个人,测试数据集中的96个。 一次性交叉验证导致我们选择k = 17的值。测试数据集上17个最近邻程序的错误率为0.35,而使用我们的程序,我们得到错误率0.29。 使用我们的方法的实质性收益可以部分地通过交叉验证过程选择的k值大大超过我们的MCMC采样器所探索的值来解释。
相比交叉验证选择k值和通过MCMC采样器实现选择的收益对比
5.结论
尽管福尔摩斯和亚当斯(2003)发起了贝叶斯分析k-最近邻方法的概率背景,本文通过在训练数据集上定义一个连贯概率模型来矫正原始技术与真实概率模型之间的联系。本文提出的方法的优点:这个新模型(3)然后为贝叶斯推理提供了一个听起来可行的设置,并且不仅评估测试数据集的最可能的分配,而且评估它们与它们的不确定性。清楚地证明了使用概率环境的优点:只有在这种情况下,才能构建如图3所示的工具,如预测图。这显然对于实验者来说是一个巨大的好处,因为可以估计最可能的类之间的界限,并且可以确定哪个区域可以被分配给特定的类或那些类是不确定的。此外,概率框架允许在标准模型选择观点中对参与类别分配的邻居数量进行自然和综合分析。这个观点可以扩展到协变量x的最重要组成部分的选择,尽管在本文中没有探讨这种可能性。
本文还讨论了与这种方法相关的计算困难,即很难求解的归一化常数的问题。虽然文献中已经彻底地讨论了这一点,但是我们对三个独立近似的比较,得出了对于适度大小的训练集,伪似然近似效果不好的结论。此外,虽然路径采样和完美取样近似值对于确定这个问题的求解是有用的,但它们不能在在实践中操作执行,但是我们还表明,Møller等人的完美采样方案的Gibbs采样替代方案这两种方案既可以实际操作又具有实用性。








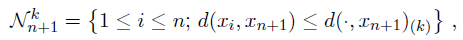

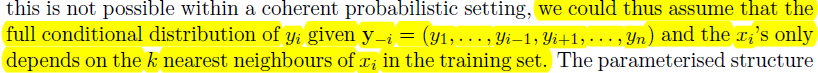
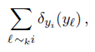

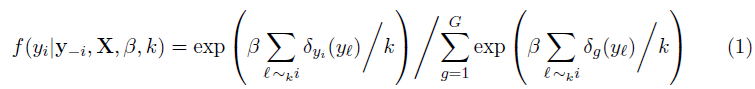



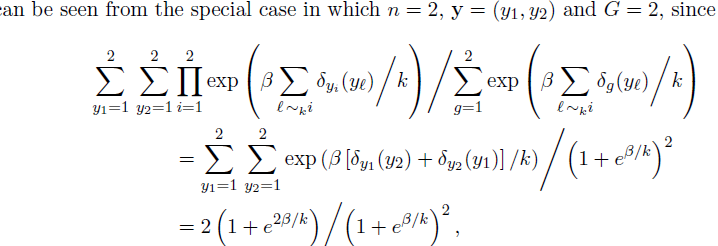
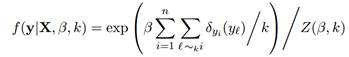
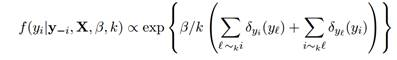


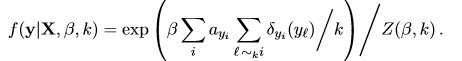


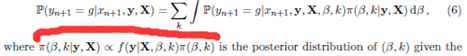



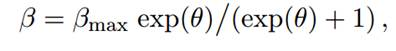
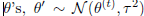

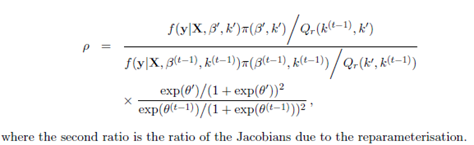


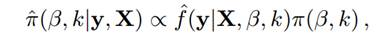
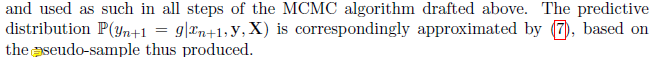

























 5344
5344

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








