【论文解读】《LIMO: Less is More for Reasoning》

k layc

已于 2025-03-09 23:10:08 修改

阅读量981

点赞数 14

文章标签：人工智能 python 机器学习语言模型 LIMO 高质量数据集

于 2025-03-09 23:08:17 首次发布

本文链接：https://blog.csdn.net/qq_30731313/article/details/146140767

版权

链接：https://arxiv.org/pdf/2502.03387

1. 摘要

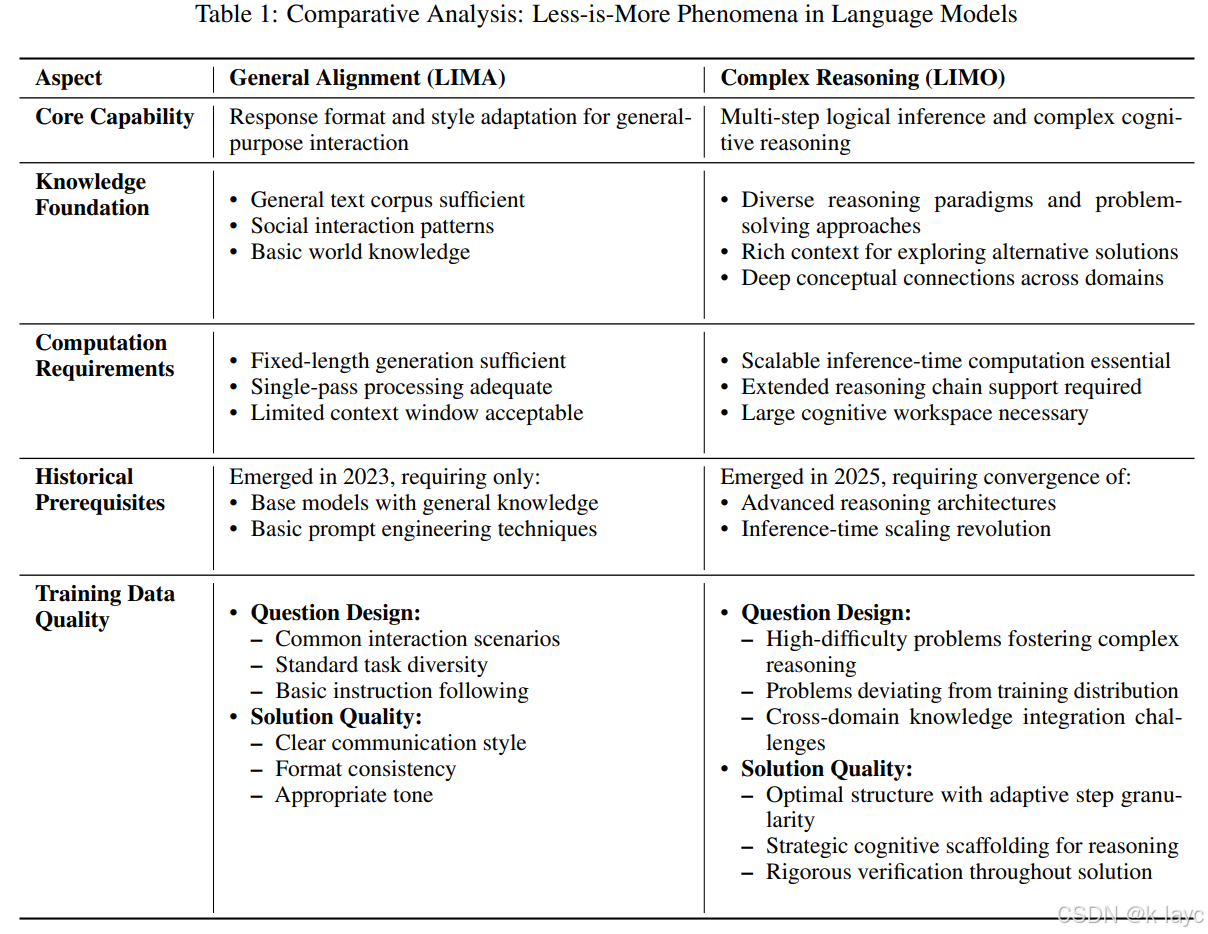
在这里插入图片描述

LIMO提出了一种颠覆性观点：复杂推理能力可通过极少量（817个）高质量示例激发，而非传统认为的需要海量数据（>100,000样本）。在AIME和MATH基准测试中，LIMO分别以57.1%和94.8%的准确率显著超越传统SFT模型，且仅需1%的训练数据。其核心贡献包括：

LIMO假设：预训练模型若已编码足够领域知识，仅需少量高质量认知模板即可激活复杂推理。
跨领域泛化：在10个多样化基准测试中，LIMO比使用100倍数据训练的模型平均提升40.5%。
开源工具：提供完整训练代码、评估流程和数据集。

2. 核心假设：LIMO Hypothesis

2.1 假设定义

$\text{复杂推理能力} = f(\text{预训练知识完整性}, \text{认知模板质量})$

预训练知识完整性：模型参数中是否已嵌入目标领域的全面知识（如数学）。
认知模板质量：示例是否展示如何系统性利用预训练知识的推理链。

2.2 与传统方法的对比

在这里插入图片描述

传统观点	LIMO观点
需海量数据防止过拟合	高质量示例>数据量
SFT导致记忆而非泛化	精心设计的SFT实现泛化

3. 方法论

3.1 数据集构建

3.1.1 问题选择标准

难度：筛选Qwen2.5-Math-7B-Instruct无法解决的问题。
多样性：覆盖代数、几何、组合数学等6大领域。
分布外特性：排除训练数据中常见的问题模式。

3.1.2 推理链质量评估

质量等级	特征	示例
L5	自我验证、多路径探索	“检查中间结果： $x = 3$ 时方程成立吗？”
L1	线性推导无验证	“解得 $x = 3$ ，故答案为3。”

4. 实验结果

在这里插入图片描述

4.1 主要基准测试

数据集	LIMO	OpenAI-o1	QwQ-32B
AIME24	57.1%	44.6%	50.0%
MATH500	94.8%	85.5%	89.8%
GPQA	66.7%	73.3%	65.1%

4.2 数据效率对比

训练数据量：817 vs 100,000样本
AIME提升：6.5% → 57.1%（817样本）
MATH提升：59.2% → 94.8%（817样本）

在这里插入图片描述
不同 LLM Backbone（Qwen1.5 vs Qwen2.5）的表现也差别明显。更强大的预训练基础会让模型的推理更稳定，避免关键逻辑漏洞。

5. 关键分析

5.1 推理链质量影响

L5 vs L1性能差：AIME任务相差15%，MATH任务相差12%。
关键特征：自我验证语句（“Wait, 24分钟=0.4小时？”）、多路径探索。

5.2 问题难度影响

简单问题（MATH Level 1-2）：准确率72%
复杂问题（AIME）：准确率提升至91.2%
机制：复杂问题强制模型整合跨领域知识。

6. 案例研究

6.1 数学问题求解对比

问题：Aya以 $s$ km/h行走9km，总耗时4小时（含咖啡店停留 $t$ 分钟）。当速度提升至 $s + 2$ km/h，总耗时2小时24分钟。求当速度为 $s+\frac{1}{2}$ 时的总耗时。

LIMO推理片段

1. 转换单位：2小时24分钟=2.4小时
2. 建立方程：
   - 情况1：9/s + t/60 = 4
   - 情况2：9/(s+2) + t/60 = 2.4
3. 消元得：9(1/s - 1/(s+2)) = 1.6
4. 解二次方程：s=2.5 km/h
5. 代入验证：t=192分钟
6. 最终计算：9/(2.5+0.5) + 192/60 = 3 + 3.2 = 6.2小时 → 372分钟