卡尔曼滤波公式及参数详解

目录

一．卡尔曼滤波介绍

二．卡尔曼滤波５大公式

0．状态方程

1．预测

2．更新

3．参数详解

4．参数设置与调整

 

---

一．卡尔曼滤波介绍

卡尔曼滤波是对输入线性系统的观测值进行最优估计的一种递归算法，在数据融合、滤波、预测等方面具有广泛的应用。我们无法建立一个完美的模型来消除系统的不确定因素，这些不确定性包括系统模型的自身缺陷、系统过程扰动（不可测也不可建模）以及得到观测数据的传感器的测量误差。这些误差往往会影响我们的估计值，所以卡尔曼滤波算法通过最小化误差方差求解卡尔曼增益，以此来进行后验估计，已达到滤波效果。卡尔曼滤波使用条件：有限维的线性系统，测量噪声和过程噪声均服从正态分布。

二．卡尔曼滤波５大公式

0．状态方程

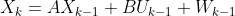
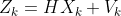
1．预测

先验估计：根据上一次最优估计的结果，预测当前时刻的估计值，由于缺失过程噪声，所以是不完整的，先验的。

先验估计协方差：

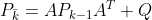
2．更新

kalman增益：先验估计值与实际值存在误差，该误差也假设符合正太分布，为了使误差最小，即求误差方差最小，通过对Ｋ求导等于０，求出Ｋ值，此时误差最小。根据调整测量误差Ｒ，可以调整增益是更相信观测还是更相信预测。

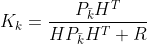
后验估计：

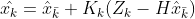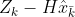　　（　代表实际观测与预测观测的残差。）

后验估计协方差：

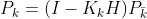
3．参数详解

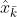• ：代表先验状态估计值，通过上一时刻最优估计值预测到当前时刻的结果。
• 和：代表后验状态估计值，为滤波后的最优估计。
• ：代表状态转移矩阵，是对状态变量的运动建模，例如匀速直线模型，弹簧阻尼模型等。
• ：代表控制矩阵（将输入转化为状态），：代表输入控制量。当系统有外加作用时，如匀加速运动模型，会有控制量，也可能没有控制量。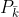
• ：代表先验估计协方差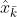（协方差），通过使它的迹最小（方差和最小）使得误差最小，以此求出卡尔曼增益。
• ：代表后验估计协方差，更新后作为下一次迭代的输入。
• ：卡尔曼增益，为观测和预测的加权系数。
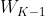• ：过程噪声协方差，由于（过程噪声）不可测，所以假设其符合正态分布，。
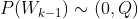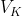• ：测量噪声协方差，由于（测量噪声）不可测，所以假设其符合正态分布，。
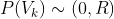• ：实际观测值。
• ：测量矩阵，把状态变量转化为预测观测值。
• 初始化：和需要进行初始化。

4．参数设置与调整

• 对于过程噪声Ｑ值，其值越小代表我们对模型预测值信任越高，系统收敛的也越快，反之相反；对于测量噪声Ｒ，其值越大代表我们对测量值信任越低，若过大此时系统表现为响应慢，过小则会出现系统震荡。调整参数时固定一个调整一个，从小到大调整Ｑ值使系统收敛速度正常，从大到小调整Ｒ值使输出结果接近真实。
• 对于Ｘ，Ｐ的初始值，其值决定了开始时的收敛速度，一般设置为与理想值相同数量级或者较小的数，以求较快的收敛，随着迭代的进行，Ｐ值会收敛为最小的估计协方差矩阵。