线性拟合3-戴明回归

上一篇是用正交回归算法来拟合直线。本文将正交回归一般化，当原始点的横纵坐标都有噪声和误差，并且噪声不同时，就可以考虑在目标函数中假如权值。这样看起来就像是斜投影，所以也可以说是优化的斜距离。

戴明回归

正交方法考虑的是自变量$x$和因变量$y$有相同方差的情况。但是更一般的，可能自变量和因变量的测量方式是不一样的，这样会造成两个方差的不同，因此应该给与不同的考虑。戴明回归就相当于求加权的正交回归，是正交回归向一般化方向的推导。
总结一下：

• 最小二乘法优化的是竖直距离；
• 正交回归优化的垂直距离；
• 戴明回归优化的是斜距离。

对比如下图所示：

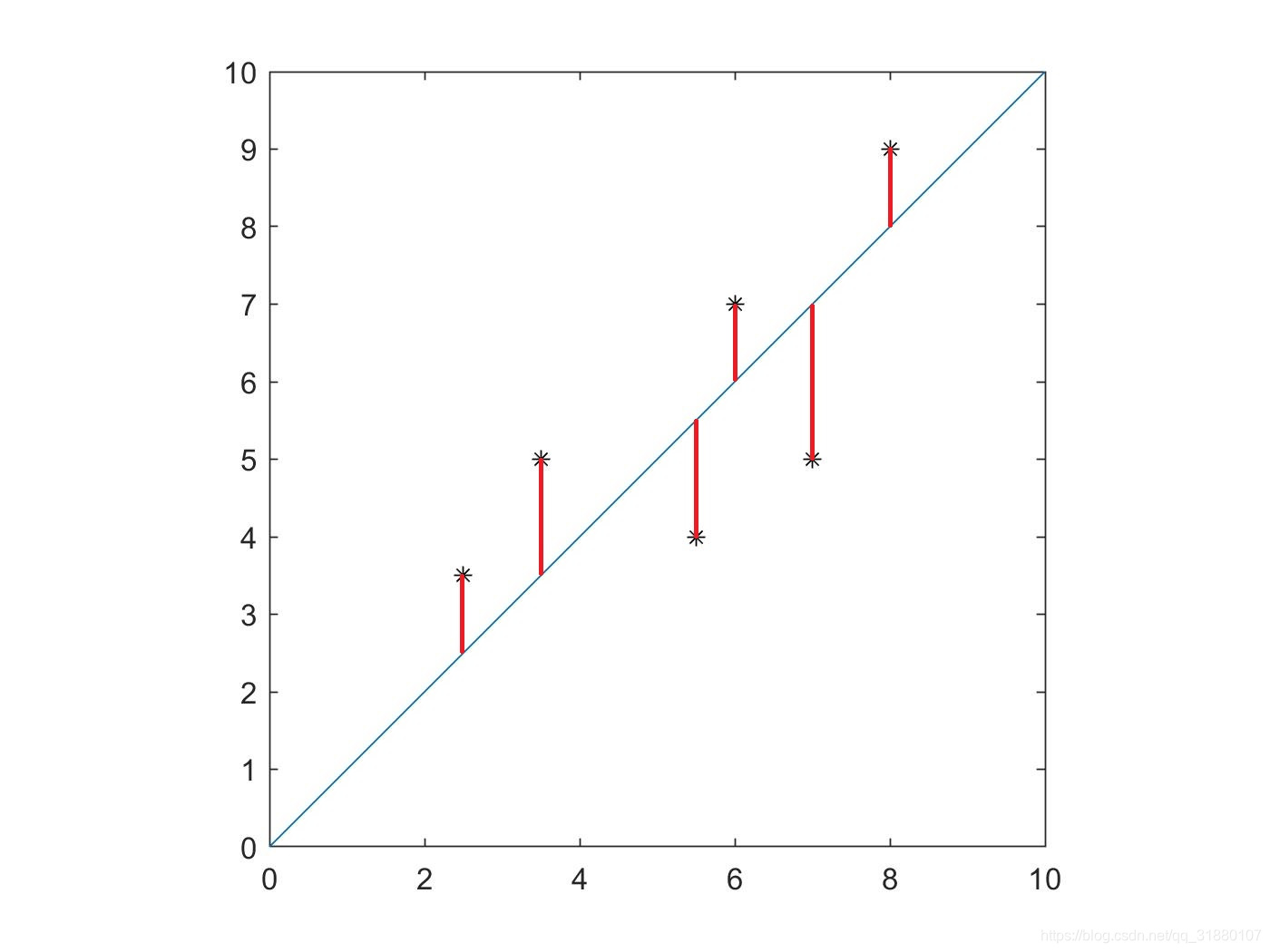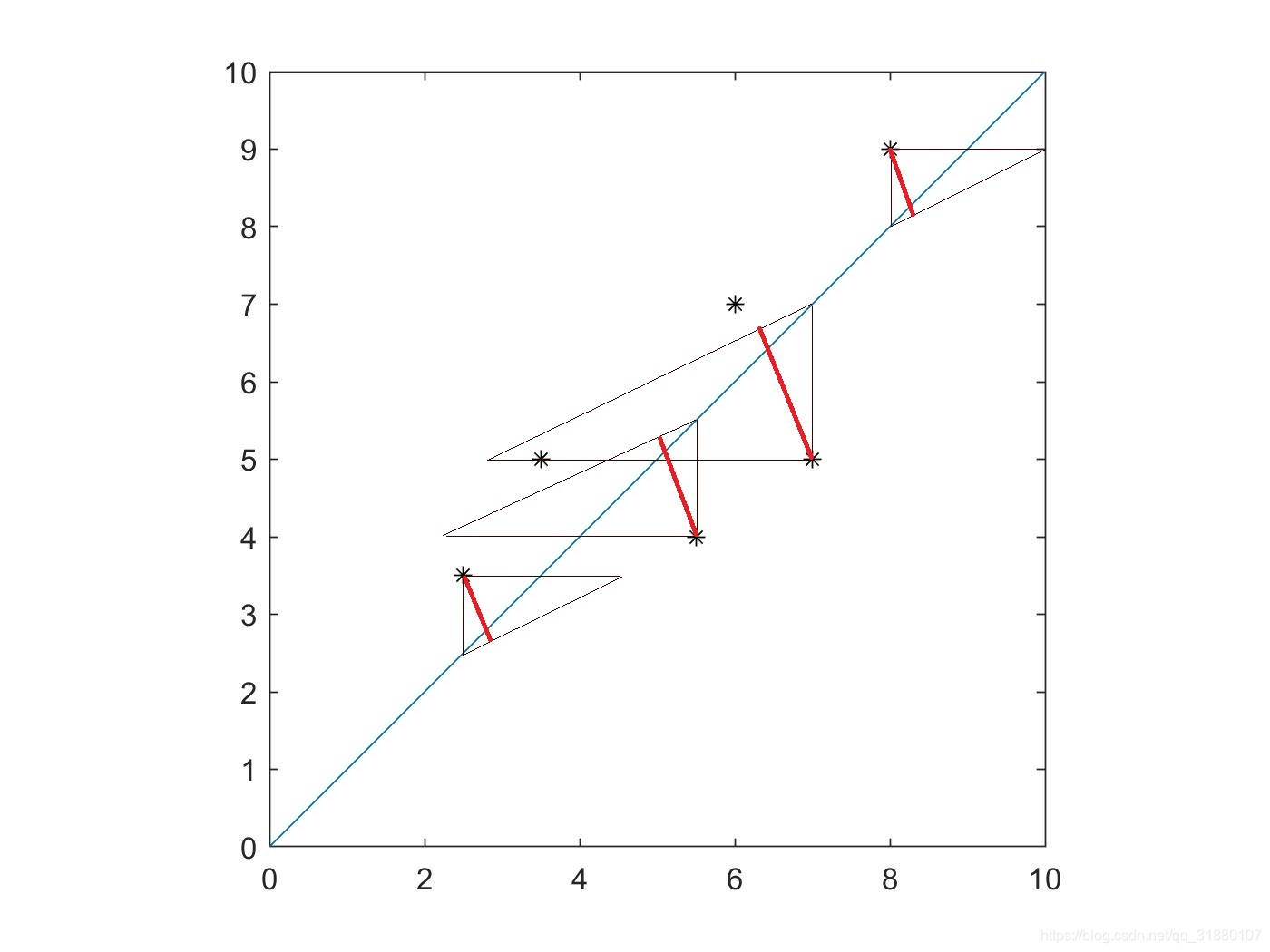最小二乘	正交回归	戴明回归

目标函数

假设${ϵ}_i$和${\eta }_i$都符合正态分布且相互独立，其方差分别为：${\mathbf{s}}_{xx}$和${\mathbf{s}}_{yy}$。定义方差比$\delta$为:
$$\delta =\frac{{\mathbf{s}}_{yy}}{{\mathbf{s}}_{xx}}$$
在大部分情况下，测量一组数据的环境和方法基本是不变的，所以同一组数据的方差应该不会变化。在后面的计算中，我们都假设它们的方差为常值，所以它们的方差比$\delta$也为常值。
同样使用直线方程$y=ax+b$来进行拟合。假设最后拟合直线的参数为$\hat{a}$和$\hat{b}$，则有：
$${\hat{y}}_i=\hat{a}{\hat{x}}_i+\hat{b}$$
目标函数可以写成：
$${\mathbf{J}}_3=\sum (\frac{{ϵ}_i^2}{{\mathbf{s}}_{yy}}+\frac{{\eta }_i^2}{{\mathbf{s}}_{xx}})=\frac{1}{{\mathbf{s}}_{yy}}\sum ((y_i-y_i^{\star }{)}^2+\delta (x_i-x_i^{\star }{)}^2)$$
因为${\mathbf{s}}_{yy}$为常数，所以可以将目标函数写成：
$${\mathbf{J}}_3=\sum [(y_i-a{x}_i^{\star }-b{)}^2+\delta (x_i-x_i^{\star }{)}^2]$$
所以最终目的是求$a$，$b$，$x_i^{\star }$的值，使得目标函数${\mathbf{J}}_3$最小。

求解结果

为了求目标函数的最小值，应该将目标函数${\mathbf{J}}_3$分别对$x_i^{\star }$，$a$，$b$求导。然后令三个式子等于0，应该就能解出三个参数的值。
推导过程有些复杂，如果感兴趣可以看文章最后的详细推导过程。
这里直接写出求解结果:
$$\{\begin{array}{rl}& \hat{a}=\frac{{\mathbf{s}}_{yy}-\delta {\mathbf{s}}_{xx}+\sqrt{({\mathbf{s}}_{yy}-\delta {\mathbf{s}}_{xx}{)}^2+4\delta {\mathbf{s}}_{xy}^2}}{2{\mathbf{s}}_{xy}}\\ & \hat{b}=\bar{y}-\hat{a}\bar{x}\\ & {\hat{x}}_i=x_i+\frac{\hat{a}}{{\hat{a}}^2+\delta }(y_i-\hat{b}-\hat{a}{x}_i)\end{array}$$
所以最后拟合曲线的斜率为$\hat{a}$，与$y$轴的截距为$\hat{b}$，而且第$i$个点的横坐标的估计值为${\hat{x}}_i$。
其中${\mathbf{s}}_{xx}$和${\mathbf{s}}_{yy}$为$x$和$y$的样本方差，${\mathbf{s}}_{xy}$为$x$和$y$的协方差。

验证正交回归

因为戴明回归是正交回归的一般化推导，所以在特殊情况下，一般回归就变为正交回归，这个特殊情况就是方差比$\delta =1$。
所以当$\delta =1$时，最后结果可以化简为：
$$\{\begin{array}{rl}& a^2({\mathbf{s}}_{xy})+a(-{\mathbf{s}}_{yy}+{\mathbf{s}}_{xx})-{\mathbf{s}}_{xy}=0\\ & b=\bar{y}-a\bar{x}\end{array}$$
这与正交回归的结果一致。

附录：详细推导过程

对$x_i^{\star }$求导:

首先对$x_i^{\star }$求导。因为是要求目标函数的最小值，应该是对任意$i$，目标函数都取最小值，所以目标函数对$x_i^{\star }$求导时，可以推导其中一个$i$：
$$\begin{array}{rl}\frac{\partial {\mathbf{J}}_2^i}{x_i^{\star }}& =\frac{\partial }{\partial x_i^{\star }}[(y_i-a{x}_i^{\star }-b{)}^2+\delta (x_i-x_i^{\star }{)}^2]\\ & =-2a(y_i-a{x}_i^{\star }-b)-2\delta (x_i-x_i^{\star })\\ & =2(-a{y}_i+a^2{x}_i^{\star }+ab-\delta x_i+\delta x_i^{\star })\end{array}$$
令$\frac{\partial {\mathbf{J}}_2^i}{x_i^{\star }}=0$，得：
$$-a{y}_i+a^2{x}_i^{\star }+ab-\delta x_i+\delta x_i^{\star }=0$$
解得：
$$x_i^{\star }=\frac{a{y}_i+\delta x_i-ab}{a^2+\delta }$$

对$b$求导:

将目标函数${\mathbf{J}}_2$对$b$求导：
$$\begin{array}{rl}\frac{\partial {\mathbf{J}}_2}{\partial b}& =\frac{\partial }{\partial b}\sum [(y_i-a{x}_i^{\star }-b{)}^2+\delta (x_i-x_i^{\star }{)}^2]\\ & =\sum (-2y_i+2a{x}_i^{\star }+2b)\end{array}$$
令$\frac{\partial {\mathbf{J}}_2}{\partial b}=0$，得：
$$-\sum y_i+a\sum x_i^{\star }+nb=0$$
解得：
$$b=\frac{1}{n}\sum (y_i-a{x}_i^{\star })$$
将上面求得的$x_i^{\star }=\frac{a{y}_i+\delta x_i-ab}{a^2+\delta }$带入，得：
$$\begin{array}{rl}b& =\frac{1}{n}\sum (y_i-a{x}_i^{\star })\\ & =\frac{1}{n}\sum (y_i-a\frac{a{y}_i+\delta x_i-ab}{a^2+\delta })\\ & =\frac{1}{n}\sum (y_i-a\frac{a{y}_i+\delta x_i}{a^2+\delta }+\frac{a^{2}b}{a^2+\delta })\end{array}$$
继续化简得：
$$\begin{array}{rl}b(1-\frac{a^2}{a^2+\delta })& =\frac{1}{n}\sum (y_i-a\frac{a{y}_i+\delta x_i}{a^2+\delta })\\ & =\frac{1}{n}\sum [y_i(1-\frac{a^2}{a^2+\delta })-x_i\frac{a\delta }{a^2+\delta }]\end{array}$$
最后解得：
$$\begin{array}{rl}b& =\frac{1}{n}\sum (y_i-x_{i}a)\\ & =\bar{y}-a\bar{x}\end{array}$$
所以，可以得：
$$b=\bar{y}-a\bar{x}$$

对$a$求导:

将目标函数${\mathbf{J}}_2$对$a$求导：
$$\begin{array}{rl}\frac{\partial {\mathbf{J}}_2}{\partial a}& =\frac{\partial }{\partial a}\sum [(y_i-a{x}_i^{\star }-b{)}^2+\delta (x_i-x_i^{\star }{)}^2]\\ & =-2\sum [(y_i-a{x}_i^{\star }-b)x_i^{\star }]\end{array}$$
令$\frac{\partial {\mathbf{J}}_2}{\partial a}=0$，得：
$$\sum [(y_i-a{x}_i^{\star }-b)x_i^{\star }]=0$$
同样，将$x_i^{\star }=\frac{a{y}_i+\delta x_i-ab}{a^2+\delta }$代入，得：
$$\sum [(y_i-b-a\frac{a{y}_i+\delta x_i-ab}{a^2+\delta })\frac{a{y}_i+\delta x_i-ab}{a^2+\delta }]=0$$
等号两边同时乘$a^2+\delta$，可以得：
∑ { [ ( y i − b ) ( a 2 + δ ) − a 2 ( y i − b ) − a δ x i ] [ δ x i + a ( y i − b ) ] } = 0 \sum\{[(y_i-b)(a^2+\delta)-a^2(y_i-b)-a\delta x_i][\delta x_i+a(y_i-b)]\}=0 ∑{[(yi​−b)(a2+δ)−a2(yi​−b)−aδxi​][δxi​+a(yi​−b)]}=0
继续化简得：
$$\begin{array}{rl}0=& a^2(b\delta \sum x_i-\sum \delta \sum x_i{y}_i)\\ +& a(b^2\delta -2b\delta \sum y_i+\delta \sum y_i^2-{\delta }^2\sum x_i^2)\\ -& b{\delta }^2\sum x_i+{\delta }^2\sum x_i{y}_i\end{array}$$
将$b=\bar{y}-a\bar{x}$带入，得：
$$\begin{array}{rl}0=& a^3(n{\bar{x}}^2-\bar{x}\sum x_i)\\ +& a^2(\bar{y}\sum x_i-\sum x_i{y}_i-2n\bar{x}\bar{y}+2\bar{x}\sum y_i)\\ +& a(\sum y_i^2+n{\bar{y}}^2-2\bar{y}\sum y_i+\delta \bar{x}\sum x_i-\delta \sum x_i^2)\\ +& \delta (\sum x_i{y}_i-\bar{y}\sum x_i)\end{array}$$
继续化简，对每一项都除以$n$，可以得：
$$\begin{array}{rl}0=& a^2(\bar{x}\bar{y}-\overline{xy}-2\bar{x}\bar{y}+2\bar{x}\bar{y})\\ +& a[\overline{y^2}+{\bar{y}}^2-2{\bar{y}}^2+\delta (\overline{x^2}-{\bar{x}}^2)]\\ +& \delta (\overline{xy}-\bar{x}\bar{y})\end{array}$$
最后化简为：
$$a^2(-{\mathbf{s}}_{xy})+a({\mathbf{s}}_{yy}-\delta {\mathbf{s}}_{xx})+\delta {\mathbf{s}}_{xy}=0$$
这是一个二元一次方程组，解得：
$$a=\frac{-({\mathbf{s}}_{yy}-\delta {\mathbf{s}}_{xx})\pm \sqrt{({\mathbf{s}}_{yy}-\delta {\mathbf{s}}_{xx}{)}^2+4\delta {\mathbf{s}}_{xy}^2}}{2{\mathbf{s}}_{xy}}$$
因为${\mathbf{s}}_{yy}-\delta {\mathbf{s}}_{xx}\le \sqrt{({\mathbf{s}}_{yy}-\delta {\mathbf{s}}_{xx}{)}^2+4\delta {\mathbf{s}}_{xy}^2}$总是成立的，所以上式分子只能是正或者负。又因为$a$的值应该与${\mathbf{s}}_{xy}$的符号保持一致，所以上式分子应该取正号。