时空图卷积ST-GCN理论和代码详解

1 前言

基于骨架的动作识别（Skeleton-Based Action Recognition）主要任务是从一系列时间连续的骨骼关键点（2D/3D）中识别出正在执行的动作。因为牵涉到骨骼框架这种图结构的输入，采用GCN的方法逐渐成为了主流，并取得了不错的效果。

在学习ST-GCN之前，我在网上找了一些GCN相关的教程与文章进行了学习，现将推荐的系列文章整理如下，大家自行翻阅：

• 比较通俗易懂的GCN解析

  （https://www.zhihu.com/question/54504471/answer/611222866）

• 比较完整的GCN解析

  （https://zhuanlan.zhihu.com/p/90470499）

这里我稍微总结下基础的GCN步骤（假设图输入为），可以视为

• 对图输入进行特征提取（假设参数为），输出。微观来看，这个特征提取可以理解为对图上每个节点的特征进行了分别提取，其特征维度从变化到；

• 根据图结构中建立一个邻接矩阵，并对其进行归一化or对称归一化，获得；

• 利用归一化的邻接矩阵对提取后的特征进行聚合，聚合的结果为。

这样一来，基本的图卷积运算就实现了。其具体的实现代码如下所示：

class GraphConvolution(nn.Module):
    def __init__(self, input_dim, output_dim, use_bias=True):
        """图卷积：L*X*\theta
        Args:
        ----------
            input_dim: int
                节点输入特征的维度
            output_dim: int
                输出特征维度
            use_bias : bool, optional
                是否使用偏置
        """
        super(GraphConvolution, self).__init__()
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.use_bias = use_bias
        self.weight = nn.Parameter(torch.Tensor(input_dim, output_dim))
        if self.use_bias:
            self.bias = nn.Parameter(torch.Tensor(output_dim))
        else:
            self.register_parameter('bias', None)
        self.reset_parameters()

    def reset_parameters(self):
        init.kaiming_uniform_(self.weight)
        if self.use_bias:
            init.zeros_(self.bias)

    def forward(self, adjacency, input_feature):
        """邻接矩阵是稀疏矩阵，因此在计算时使用稀疏矩阵乘法
    
        Args: 
        -------
            adjacency: torch.sparse.FloatTensor
                邻接矩阵
            input_feature: torch.Tensor
                输入特征
        """
        device = "cuda" if torch.cuda.is_available() else "cpu"
        support = torch.mm(input_feature, self.weight.to(device))
        output = torch.sparse.mm(adjacency, support)
        if self.use_bias:
            output += self.bias.to(device)
        return output

言归正传，我们先从ST-GCN说起，其论文名和代码链接如下：

• 论文名：Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition

• 代码地址：https://github.com/yysijie/st-gcn

网上也有部分小伙伴做了相关的解析，觉得挺不错的，链接如下：

https://www.zhihu.com/question/276101856/answer/638672980

下面我们将从（1）数据输入（2）网络结构两方面，通过结合论文和代码对ST-GCN进行解析。

2. 数据输入

2.1 数据结构

基于骨架的动作识别方法的一般输入为时间连续的人体骨架关键点，如下图1所示。

图1

这些关键点可以通过openpose进行姿态估计获取，也可以手动标注。其数据维度一般为（N, C, T, V, M ），其中（参考上述引用知乎文章）：

“

• N代表视频的数量，通常一个 batch 有 256 个视频（其实随便设置，最好是 2 的指数）；

• C代表关节的特征，通常一个关节包含x,y,acc 等 3 个特征（如果是三维骨骼就是 4 个），x,y为节点关节的位置坐标，acc为置信度。

• T 代表关键帧的数量，一般一个视频有 150 帧。

• V 代表关节的数量，通常一个人标注 18 个关节。

• M代表一帧中的人数，一般选择平均置信度最高的 2 个人。

需要注意C（特征），T（时间），V（空间）。

2.2 数据预处理

事实上，上述输入数据（N, C, T, V, M ）在输入至ST-GCN网络之前需要进行标准化操作。

该标准化是在时间维度上进行的，具体来说，就是标准化某节点在所有T个关键帧的特征值。其具体实现代码如下：

# data normalization
N, C, T, V, M = x.size()
x = x.permute(0, 4, 3, 1, 2).contiguous()
x = x.view(N * M, V * C, T)
x = self.data_bn(x)
x = x.view(N, M, V, C, T)
x = x.permute(0, 1, 3, 4, 2).contiguous()
x = x.view(N * M, C, T, V)

其中函数data_bn定义如下：

self.data_bn = nn.BatchNorm1d(in_channels * A.size(1))

2.3 图划分策略

在ST-GCN这篇文章中，作者的另一大创新点是通过对运动的分析引入了图划分策略，即建立多个反应不同运动状态（如静止，离心运动和向心运动）的邻接矩阵。作者在原文中提到其采用了三种不同的策略，分别为：

• Uni-labeling，即与跟根节点相邻的所有结点具有相同的label，如下图b所示。

• Distance partitioning，即根节点本身的label设为0，其邻接点设置为1，如下图c所示。

• Spatial configuration partitioning，是本文提出的图划分策略。也就是以根节点与重心的距离为基准（label=0），在所有邻接节点到重心距离中，小于基准值的视为向节心点（label=1），大于基准值的视为离心节点（label=2）。

图2

具体的代码实现如下：

A = []
for hop in valid_hop:
    a_root = np.zeros((self.num_node, self.num_node))
    a_close = np.zeros((self.num_node, self.num_node))
    a_further = np.zeros((self.num_node, self.num_node))
    for i in range(self.num_node):
        for j in range(self.num_node):
            if self.hop_dis[j, i] == hop:
                if self.hop_dis[j, self.center] == self.hop_dis[
                        i, self.center]:
                    a_root[j, i] = normalize_adjacency[j, i]
                elif self.hop_dis[j, self.
                                  center] > self.hop_dis[i, self.
                                                         center]:
                    a_close[j, i] = normalize_adjacency[j, i]
                else:
                    a_further[j, i] = normalize_adjacency[j, i]
    if hop == 0:
        A.append(a_root)
    else:
        A.append(a_root + a_close)
        A.append(a_further)
A = np.stack(A)

值得注意的是，hop类似于CNN中的kernel size。hop=0就是根节点自身，hop=1表示根节点与其距离等于1的邻接点们，也就是上图（a）的红色虚线框。

为了便于更好理解代码，我们默认上述两个循环中的为根节点。因为条件***if self.hop_dis[j, i] == hop***限制，可以视为根节点的本身（hop=0）或者其邻接节点（hop=1）。

3. 网络结构

骨架输入数据具有时间与空间属性，这些属性对运动检测至关重要。因此提出ST-GCN应当具备能够从时空维度提取特征的能力，其在GCN中的表现就是能够同时聚合时空维度的信息，如下图所示。

图3

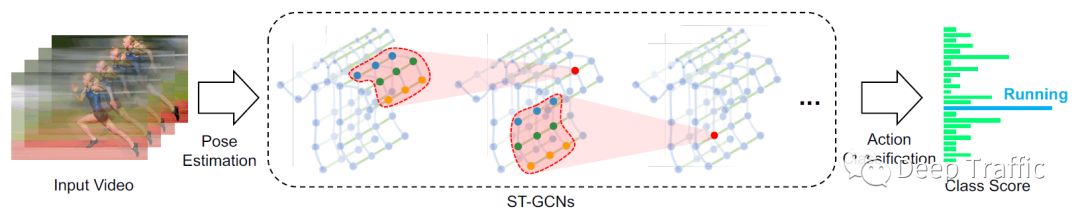
更具体地，我们给出了ST-GCN具体的结构图，如下图所示。

图4

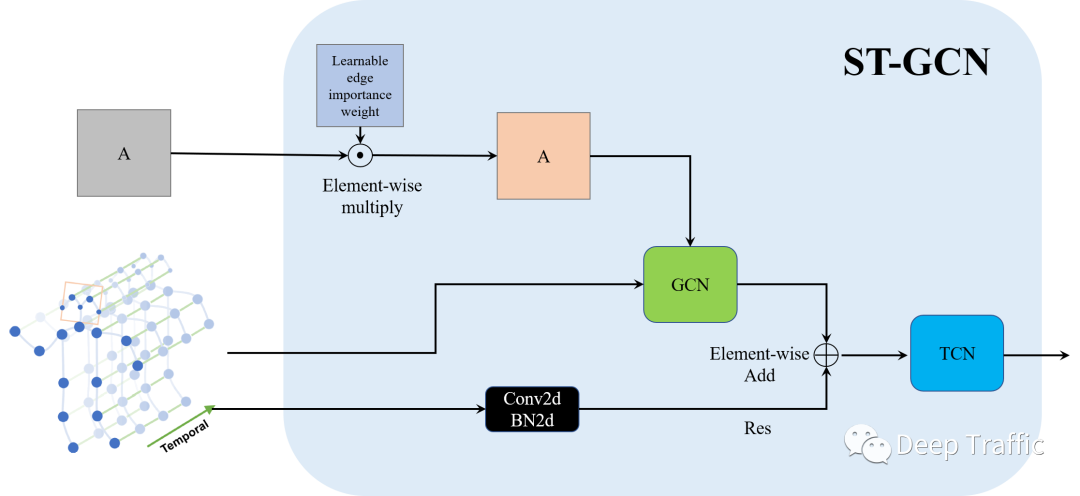
其具体可以分为以下步骤：

• 步骤1：引入一个可学习的权重矩阵（与邻接矩阵等大小）与邻接矩阵按位相乘。该权重矩阵叫做“Learnable edge importance weight”，用来赋予邻接矩阵中重要边（节点）较大的权重且抑制非重要边（节点）的权重。

• 步骤2：将加权后的邻接矩阵与输入送至GCN中进行运算。同时，作者还引入了残差结构（一个CNN+BN）计算获得Res，与GCN的输出按位相加，实现空间维度信息的聚合。

• 步骤3：利用TCN网络（实际上是一种普通的CNN，在时间维度的kernel size>1）实现时间维度信息的聚合。

上述ST-GCN模块的代码实现如下：

def forward(self, x, A):

    res = self.residual(x)
    x, A = self.gcn(x, A)
    x = self.tcn(x) + res

    return self.relu(x), A

• 其中残差结构self.residual定义如下：

self.residual = nn.Sequential(
    nn.Conv2d(
        in_channels,
        out_channels,
        kernel_size=1,
        stride=(stride, 1)),
    nn.BatchNorm2d(out_channels),
)

• GCN定义如下：

self.conv = nn.Conv2d(
        in_channels,
        out_channels * kernel_size,
        kernel_size=(t_kernel_size, 1),
        padding=(t_padding, 0),
        stride=(t_stride, 1),
        dilation=(t_dilation, 1),
        bias=bias)

def forward(self, x, A):
    assert A.size(0) == self.kernel_size

    x = self.conv(x)

    n, kc, t, v = x.size()
    x = x.view(n, self.kernel_size, kc//self.kernel_size, t, v)
    x = torch.einsum('nkctv,kvw->nctw', (x, A))

    return x.contiguous(), A

• TCN定义如下

  self.tcn = nn.Sequential(
      nn.BatchNorm2d(out_channels),
      nn.ReLU(inplace=True),
      nn.Conv2d(
          out_channels,
          out_channels,
          (kernel_size[0], 1),
          (stride, 1),
          padding,
      ),
      nn.BatchNorm2d(out_channels),
      nn.Dropout(dropout, inplace=True),
  )

实际上，本文提出模通过不断堆叠ST-GCN从图结构输入中持续提取高级的语义特征，具体如下：

self.st_gcn_networks = nn.ModuleList((
    st_gcn(in_channels, 64, kernel_size, 1, residual=False, **kwargs0),
    st_gcn(64, 64, kernel_size, 1, **kwargs),
    st_gcn(64, 64, kernel_size, 1, **kwargs),
    st_gcn(64, 64, kernel_size, 1, **kwargs),
    st_gcn(64, 128, kernel_size, 2, **kwargs),
    st_gcn(128, 128, kernel_size, 1, **kwargs),
    st_gcn(128, 128, kernel_size, 1, **kwargs),
    st_gcn(128, 256, kernel_size, 2, **kwargs),
    st_gcn(256, 256, kernel_size, 1, **kwargs),
    st_gcn(256, 256, kernel_size, 1, **kwargs),
))

# initialize parameters for edge importance weighting
if edge_importance_weighting:
    self.edge_importance = nn.ParameterList([
        nn.Parameter(torch.ones(self.A.size()))
        for i in self.st_gcn_networks
    ])
else:
    self.edge_importance = [1] * len(self.st_gcn_networks)

# ST-GCN与可学习的权重矩阵不断重复与堆叠
for gcn, importance in zip(self.st_gcn_networks, self.edge_importance):
 x, _ = gcn(x, self.A * importance)

之后，和一般的分类任务类似，作者引入了全局平均池化以及全卷积层输出预测分支，如下：

# global pooling
x = F.avg_pool2d(x, x.size()[2:])
x = x.view(N, M, -1, 1, 1).mean(dim=1)

# prediction
x = self.fcn(x)
x = x.view(x.size(0), -1)

至此，通过代码我们就很容易理解ST-GCN的具体网络结构了。

总结

至此，关于ST-GCN的解析就完毕了，希望能够帮助到大家！也欢迎大家关注我的微信公众号！

推荐阅读：

我的2022届互联网校招分享

我的2021总结

浅谈算法岗和开发岗的区别

互联网校招研发薪资汇总

对于时间序列，你所能做的一切.

什么是时空序列问题？这类问题主要应用了哪些模型？主要应用在哪些领域？

公众号：AI蜗牛车

保持谦逊、保持自律、保持进步

发送【蜗牛】获取一份《手把手AI项目》（AI蜗牛车著）

发送【1222】获取一份不错的leetcode刷题笔记

发送【AI四大名著】获取四本经典AI电子书