【transformer】|On the Relationship between Self-Attention and Convolutional Layers

transformer的提出对NLP领域的研究有很大的促进作用，得益于attention机制，特别是self-attention，就有研究学者将attention/self-attention机制引入计算机视觉领域中，也取得了不错的效果[1][2]。该论文[4]侧重于从理论和实验去验证self-attention[3]可以代替卷积网络独立进行类似卷积的操作，给self-attention在图像领域的应用奠定了坚实的基础

Ramachandran在19年的研究中，用full attention model达到了resnet baseline的精度，模型参数和计算量相比卷积网络减轻了不少

因此，论文主要研究self-attention layer在图片处理上是否能达到convolutional layer的效果，贡献如下：

在理论层面，论文通过构造性证明self-attention layers能够替代任何卷积层
在实际层面，论文通过构造multi-head self-attention layer进行实验，证明attention-only架构的前几层的确学习到了关注query pixel附近的g网格区域特征

多头自注意力层

CNN和自注意力层的主要区别是，一个像素的新值依赖于图像的其他像
素。
相对于感受野(receptive field)是K x K领域网格的卷积层，自注意力的感受野始终是全图像。

定义$X\in {\mathbb{R}}^{T\times Din}$为输入矩阵，包含$T$个$Din$维的token，在NLP中，token对应着序列化的词，同样地也可以对应序列化的像素

self-attention layer从$Din$到$Dout$的计算如公式1,2所示，

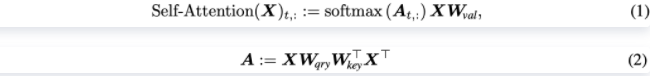
$A$为attention scores，softmax将score转换为attention probabilities，该层的参数包含查询矩阵(query matrix)$Wqry\in {\mathbb{R}}^{Din\times Dk}$，关键词矩阵(key matrix)$Wkey\in {\mathbb{R}}^{Din\times D_k}$，值矩阵(value matrix)$Wval\in {\mathbb{R}}^{Din\times Dout}$，都用于对输入进行变化，基本跟NLP中的self-attention一致

  因为只考虑相关性，self-attention一个很重要的属性是，不管输入的顺序如何改变，输出都是不变的，这对于希望顺序对结果有影响的case影响很大，因此在self-attention基础上为每个token学习一个positional encoding参数，$P\in {\mathbb{R}}^{T\times D_{in}}$为包含位置信息的embedding向量，可以有多种形式
  这里采用multiple heads版本的self-attention，每个head的参数矩阵都不一样，能够提取不同的特征，$Nh$个head输出$D_h$维结果concat后映射成$Dout$维的最终输出，两个新参数，映射矩阵(projection matrix)$Wout\in {\mathbb{R}}^{N_h{D}_h\times Dout}$，偏置$bout\in {\mathbb{R}}^{Dout}$

Attention for images

卷积是最适合神经网络的图片操作方法，给予图片$X\in {\mathbb{R}}^{W\times H\times Din}$，卷积在$(i,j)$的操作如公式5，$W\in {\mathbb{R}}^{K\times K\times Din\times Dout}$，$b\in {\mathbb{R}}^{Dout}$，K为卷积核的大小

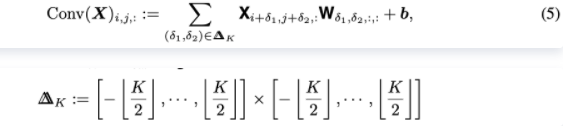
  在图片上应用self-attention，定义查询像素和关键词像素$q,k\in W\times H$.    输入的向量大小为$X\in {\mathbb{R}}^{W\times H\times Din}$
    为了保持一致性，用1D的符号来代表2D坐标，比如$p=(i,j)$，用$X_p$代表$Xij$，用$Ap$代表$Aij$
 

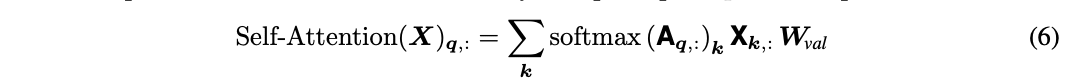
Positional encoding for images

位置编码目前主要有两种，分别是绝对位置(absolute)编码和相对(relative)位置编码
  在绝对位置编码中，每个像素拥有一个位置向量$P_p$(学习的或固定的)，于是公式2可以转换为公式7
相对位置编码的核心是只考虑查询像素和查询像素之间的位置差异，如公式8，大体是将公式7的每一项的绝对位参数改为相对位置参数。attention scores只跟偏移$\delta :=k-q$，$u$和$v$是learnable参数，每个head都不一样，而每个偏移的相对位置编码$r\delta \in {\mathbb{R}}^{D_p}$是head共享的。关键词权重分成了两部分，$Wkey$属于输入，${\hat{W}}_{key}$属于偏移
  公式9称为二次编码(quadratic encoding)，参数${\Delta }^{(h)}=({\Delta }_1^{(h)},{\Delta }_2^{(h)})$和${\alpha }^{(h)}$分别代表中心点以及attention区域的大小，都是通过学习得来的，而$\delta =({\delta }_1,{\delta }_2)$则是固定的，代表查询像素和关键词像素的相对位移

Self-attention as a convolutional layer

  定理1，对于multi-head self-attention，$Nh$个head，每个head输出$D_h$维，整体最终输出$Dout$，相对位置编码$Dp\ge 3$维，可以表示任何卷积，核大小为$\sqrt{N_h}\times \sqrt{N_h}$，output channel为$min(D_h,Dout)$

对于output channel不是固定$Dout$，论文认为当$D_h<Dout$时，$Wout$相当于一个升维操作，这个操作的特征提取不能代表原始卷积的属性，实际中，一般采用$D_h=Dout，$

上面的定理表明，在选择适当的参数后，multi-head self-attention layer可以表现得跟卷积层一样，每个head的attention score关注不同偏移距离的像素，偏移值分别在集合${\Delta }_K=-\lfloor K/2\rfloor ,...,\lfloor K/2\rfloor$内，这样整体就类似于$K\times K$核，如图1所示
卷积神经网络不止卷积核大小这个超参，还有很多其它超参，这里论文对输出的数值的一致性上进行了解释：

Padding: multi-head self-attention layer默认使用"SAME"的填充模式，而卷积层会减小K-1个像素的图片大小，因此，为了减少边界影响，可以对卷积图片进行$\lfloor K/2\rfloor$的零填充
Stride: 卷积神经网络的步长可以认为是在卷积后面加入一个pooling操作，而Theorem 1默认步长为1，但可以在后面接个pooling达到相同的结果
Dilation: 因为multi-head self-attention可以设置任意的偏移值，因此也可以代表空洞卷积

ref
https://cloud.tencent.com/developer/article/1579458
https://zhuanlan.zhihu.com/p/104026923

https://www.cnblogs.com/shiyublog/p/11236212.html