本文编辑:调皮哥的小助理
4.1介绍
雷达的频率覆盖范围很广,本文讨论了在目标探测和定位中使用的各种雷达波形,内容十分重要,各位读者需要静下心来细嚼慢咽,相信只要用心,必定有所收获。
4.2波形类型简介
在设计雷达系统之前,必须对系统的特性做出关键的选择,其中就包括雷达波形。波形不仅决定了用于处理接收信号的算法类型,而且对系统硬件单元的成本以及复杂性有影响。
一般来说,雷达波形的分类法将它们分为连续波或脉冲波。 连续波通常需要单独的接收和发射天线。 隔离要求限制了发射功率,但距离估计一般不受影响。
之前说大多数毫米波雷达的发射功率大多都在12dBm,除了EIRP还跟隔离度有关。
EIRP:等效全向辐射功率(equivalent isotropically radiated power,EIRP),或叫有效全向辐射功率,是无线电通信领域的一个常见概念,它指的是卫星、雷达或地面站在某个指定方向上的辐射功率,理想状态下等于功放的发射功率天线的增益。
另一方面,对于脉冲信号,同一天线可用于发射和接收,功率限制有所放宽,但会产生盲区,在选择波形时必须权衡利弊。
更进一步讲,调制技术会进一步区分最后使用的波形类型。在通信系统中,振幅调制、相位调制以及频率调制可以应用于波形。另外,极化的选择对接收信号的处理也有很大的影响,在下面我们将介绍最常用的雷达波形及其特性。

(图1 速度检测的连续波实例)
4.3连续波形(CW)
图1所示的单频连续波雷达只能测速,无法测距,这个结论很重要。 频率分辨率为 Δ f = 1 / T c w \Delta f=1 / T_{c w} Δf=1/Tcw,其中 T c w T_{c w} Tcw 是连续波的周期。
4.4脉冲多普勒雷达波形(PDR)
使用脉冲多普勒雷达,良好的距离分辨率和多普勒分辨率。它们分别由
Δ
f
=
1
N
p
∗
T
p
\Delta f=\frac{1}{N_p * T_p}
Δf=Np∗Tp1和
Δ
R
=
c
∗
T
p
/
2
\Delta R=c * T_p / 2
ΔR=c∗Tp/2 给出,其中
N
p
N_p
Np 是脉冲数,
T
p
T_p
Tp 是脉冲宽度,并且
c
c
c是光速。 图 2 是 PDR 波形的示例。
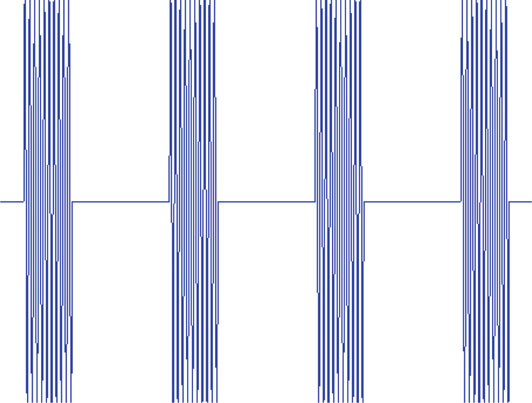
(图2 脉冲多普勒雷达示例(用于距离和速度探测的PDR波形)
4.5调频连续波 (FMCW)及其变化
FMCW是最常用的波形之一,因为它可以以更低成本的设备估计距离和速度,虽然脉冲多普勒雷达可以实现相同的功能,但系统设计复杂,成本也很高。用商人的思维来讲就是:宁可少花一块钱,也要选择成本低的。
4.5.1线性调频连续波(LFMCW)
由于目标距离和多普勒频移产生一个拍频,拍频的分量由下列表达式给出:
f
b
=
B
T
s
∗
2
R
c
f_b=\frac{B}{T_s} * \frac{2 R}{c}
fb=TsB∗c2R
f
D
=
2
v
r
λ
f_D=\frac{2 v_r}{\lambda}
fD=λ2vr(4.1)
关于这部分公式的推导,可以查看下面的文章:
调皮连续波:雷达原理 | 用MATLAB信号处理是如何解算目标的距离和速度信息的?
它们叠加成上下chirp的差频分别是
f
b
u
f_{b u}
fbu 和
f
b
d
f_{b d}
fbd ,如图3所示。
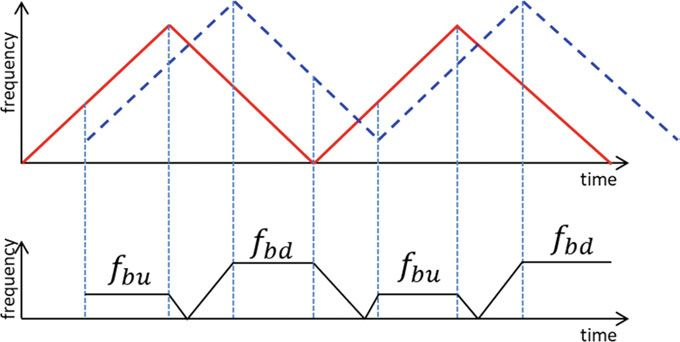
(图3 用于距离和速度检测的LFMCW示例)
f b u = f b − f d f b d = f b + f d \begin{aligned} f_{b u} &=f_b-f_d \\ f_{b d} &=f_b+f_d \end{aligned} fbufbd=fb−fd=fb+fd(4.2)
从方程式(4.2)可以估计出目标距离和径向速度为:
R
=
c
T
s
4
B
∗
(
f
b
d
+
f
b
u
)
R=\frac{c T_s}{4 B} *\left(f_{b d}+f_{b u}\right)
R=4BcTs∗(fbd+fbu)
v
r
=
λ
4
(
f
b
d
−
f
b
u
)
v_r=\frac{\lambda}{4}\left(f_{b d}-f_{b u}\right)
vr=4λ(fbd−fbu)(4.3)
FMCW:虚假(ghost)目标
对于单目标场景,通常从上下chirp得到的距离-速度谱的交集提取目标距离和速度,如图4a所示。对于多个目标,距离-速度谱的多次相交会产生虚假目标,如图4b所示。
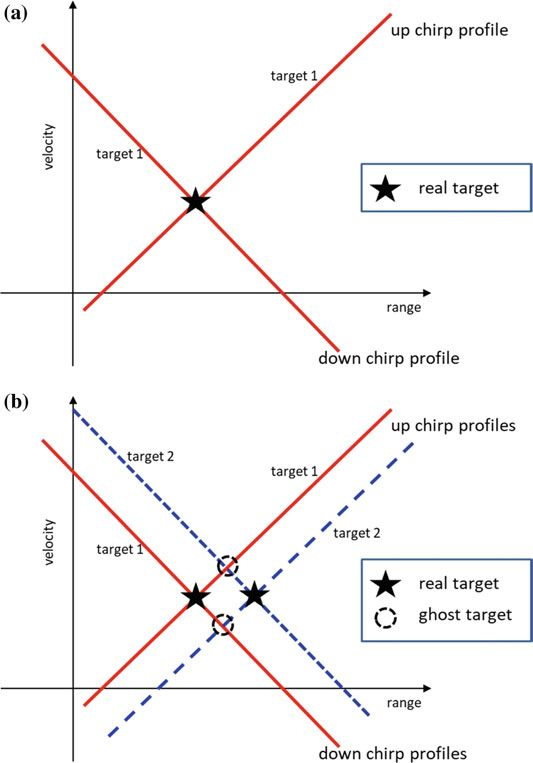
(图4 LFMCW单目标距离-速度谱示例。目标距离和速度可以明确地提取出来,b来自LFMCW的多目标距离-速度谱示例,虚假目标来自不同目标之间的多个交点)
在汽车航行中出现严重问题的虚假目标会导致错误的距离和速度,错误的位置会导致致命的车祸,增加了位置判断的风险。
4.5.2 步进FMCW
步进FMCW 雷达系统发射不同频率的一系列正弦波,并在每个离散频率上测量雷达通道引起的稳定幅值和相移。步进FMCW可以简化信号处理技术,因为可以使用固定的稳定频率 。 具体来说,可以使用逆离散傅里叶变换 (IDFT) 计算目标的距离,这可以通过快速 FFT 算法来实现。 图5给出了步进 FMCW 方案。
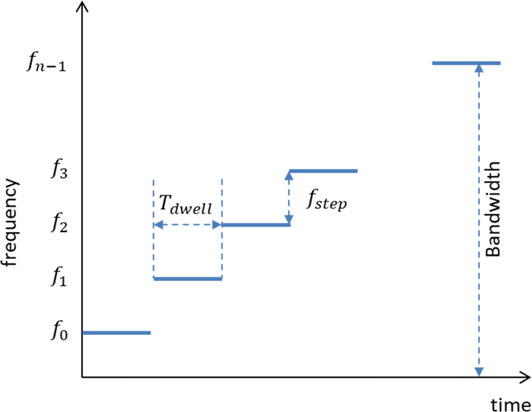
(图5 用于距离和速度检测的步进FMCW示例)
在距离
R
R
R 处来自目标的反射信号的相位由下式给出:
φ
=
2
π
f
c
∗
2
R
c
\varphi=2 \pi f_c * \frac{2 R}{c}
φ=2πfc∗c2R(4.4)
由式(4.4)可以提取距离为:
R = c φ 4 π f c R=\frac{c \varphi}{4 \pi f_c} R=4πfccφ(4.5)
但是在高频下最大不模糊距离 R max R_{\max } Rmax 太小,特别是对于汽车应用。 例如,以 2 π 2 \pi 2π 的最大可能相位为例,中心频率为 77 GHz 的相应最大距离为:
R max = c φ 4 π f c = 2 π ∗ 3 × 1 0 8 4 π ∗ 77 × 1 0 9 = 3 77 ∗ 2 ∗ 10 = 0.195 c m R_{\max }=\frac{c \varphi}{4 \pi f_c}=\frac{2 \pi * 3 \times 10^8}{4 \pi * 77 \times 10^9}=\frac{3}{77 * 2 * 10}=0.195 \mathrm{~cm} Rmax=4πfccφ=4π∗77×1092π∗3×108=77∗2∗103=0.195 cm(4.6)
这显然对许多应用程序没有实际用途。但是,如果两个中心频率 f 1 f_1 f1 和 f 2 f_2 f2 ,那么对于距离 R R R 的目标,由两个频率得到的相位为:
φ 1 = 2 π f 1 ∗ 2 R c φ 2 = 2 π f 2 ∗ 2 R c \begin{aligned} \varphi_1 &=2 \pi f_1 * \frac{2 R}{c} \\ \varphi_2 &=2 \pi f_2 * \frac{2 R}{c} \end{aligned} φ1φ2=2πf1∗c2R=2πf2∗c2R(4.7)
相位差 Δ φ \Delta \varphi Δφ 变为:
Δ φ = φ 2 − φ 1 = 4 π R c ( f 2 − f 1 ) = 4 π R c Δ f \Delta \varphi=\varphi_2-\varphi_1=\frac{4 \pi R}{c}\left(f_2-f_1\right)=\frac{4 \pi R}{c} \Delta f Δφ=φ2−φ1=c4πR(f2−f1)=c4πRΔf(4.8)
其中 Δ f = f 2 − f 1 \Delta f=f_2-f_1 Δf=f2−f1 是步进频率,由上式(4.8)可以估计出距离为:
R = c Δ φ 4 π Δ f R=\frac{c \Delta \varphi}{4 \pi \Delta f} R=4πΔfcΔφ(4.9)
对于 2 π 2 \pi 2π 的最大可能相位差,则最大距离为:
R max = 2 π c 4 π Δ f = c 2 Δ f R_{\max }=\frac{2 \pi c}{4 \pi \Delta f}=\frac{c}{2 \Delta f} Rmax=4πΔf2πc=2Δfc(4.10)
对于步进频率为10MHz,则最大距离为:
R max = 3 × 1 0 8 2 × 10 × 1 0 6 = 15 m R_{\max }=\frac{3 \times 10^8}{2 \times 10 \times 10^6}=15 \mathrm{~m} Rmax=2×10×1063×108=15 m(4.11)
可以设定一个目标的最大距离,选择合适的步进频率值,这就是步进FMCW波形法距离估计的基本原理。这部分内容和脉冲雷达参差重频解距离模糊有异曲同工之妙。
4.5.3 多频移键控(MFSK)
MFSK波形提供了同时测量明确范围和速度的可能性,如图6所示,使用了两个相互交织并移位的频率A和B。基于从 f A f_A fA 和 f B f_B fB测量的距离谱的相位差和步进频率,其距离 R R R 可以估计为:
R = − c Δ φ 4 π f step R=\frac{-c \Delta \varphi}{4 \pi f_{\text {step }}} R=4πfstep −cΔφ(4.12)
其中,
Δ
φ
=
f
B
−
f
A
\Delta \varphi=f_B-f_A
Δφ=fB−fA 是相位差。
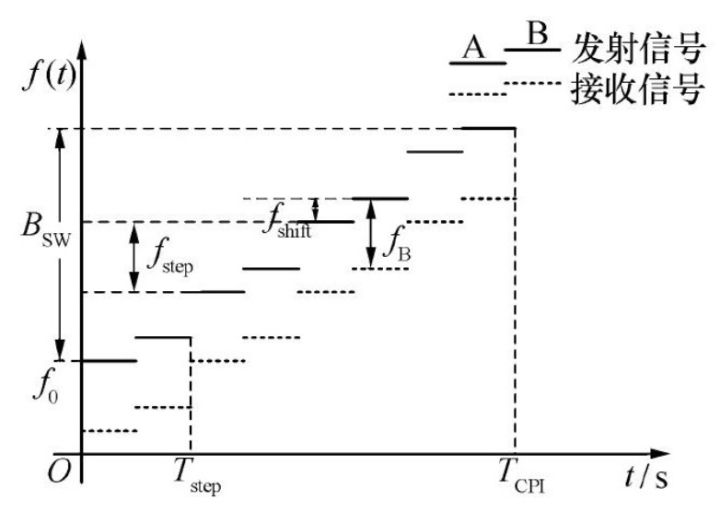
(图6 用于距离和速度检测的MFSK波形示例,采用两个频率步长A和B)
具体原理可以参考下面文献:
[1]蒋留兵,宋永坤,车俐.一种MFSK车载雷达距离速度测量方法[J].现代雷达,2017,39(11):27-33.DOI:10.16592/j.cnki.1004-7859.2017.11.006.
从FFT频谱中,可以估计两个频率的峰值将在 N peak N_{\text {peak }} Npeak 表示的同一个Bin(距离仓)处检测到,下面的表达式定义了距离和速度中的模糊。
N peak = v Δ v − R Δ R N_{\text {peak }}=\frac{v}{\Delta v}-\frac{R}{\Delta R} Npeak =Δvv−ΔRR(4.13)
其中 Δ v \Delta v Δv 是速度分辨率, Δ R \Delta R ΔR 是距离分辨率, 相位差由下式给出:
Δ φ = v Δ v ∗ ( π N − 1 ) − 2 f shift c ∗ 2 π R \Delta \varphi=\frac{v}{\Delta v} *\left(\frac{\pi}{N-1}\right)-\frac{2 f_{\text {shift }}}{c} * 2 \pi R Δφ=Δvv∗(N−1π)−c2fshift ∗2πR(4.14)
其中,N是FFT点数。
将速度表达式代入(4.14)得到最大不模糊距离为:
R unamb = c Δ R π ( N − 1 ) ∗ Δ φ − N peak ∗ π c − 4 ( N − 1 ) Δ R f shift . R_{\text {unamb }}=\frac{c \Delta R}{\pi} \frac{(N-1) * \Delta \varphi-N_{\text {peak }} * \pi}{c-4(N-1) \Delta R f_{\text {shift }}} . Runamb =πcΔRc−4(N−1)ΔRfshift (N−1)∗Δφ−Npeak ∗π.(4.15)
同理,最大不模糊速度可以表示为:
v unamb = ( N − 1 ) Δ v π ( c Δ φ − 4 π Δ R f shift N peakk ) c − 4 ( N − 1 ) Δ R f shift v_{\text {unamb }}=\frac{(N-1) \Delta v}{\pi} \frac{\left(c \Delta \varphi-4 \pi \Delta R f_{\text {shift }} N_{\text {peakk }}\right)}{c-4(N-1) \Delta R f_{\text {shift }}} vunamb =π(N−1)Δvc−4(N−1)ΔRfshift (cΔφ−4πΔRfshift Npeakk )(4.16)
由上述可以看出,从频谱得到的相移信息 Δ φ \Delta \varphi Δφ 就足以清楚地估计目标的距离和速度。
4.5.4 间断FMCW(FMICW)
FMICW 解决了发射器和接收器之间的隔离问题, 这可以通过仅在开关信号关闭时启用接收来实现,如图 7 所示。
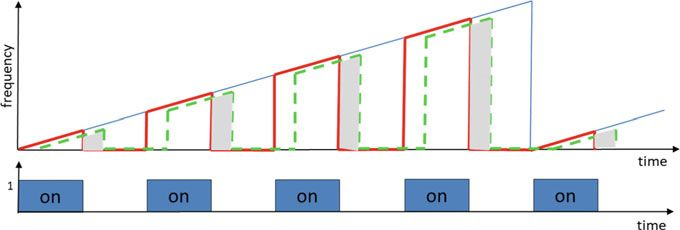
(图7用于距离和速度检测的FMICW示例。蓝色的波形是原始的不间断波形,红色为发射波形,绿色虚线为反射波形)
仅当定时信号关闭且接收波形由阴影部分显示时才允许接收, 从图 7 可以看出,对于近距离目标,总接收时间显着减少,使得近距离目标难以检测;对于远程目标,效果则相反。
因此,这种方法必须在短程目标和远程目标之间做出折衷,当目标的往返延迟是切换周期的倍数时,接收信号功率为零,导致盲区, 为避免这种现象,应选择开关频率 f s f_s fs 为:
f s = c 4 R max f_s=\frac{c}{4 R_{\max }} fs=4Rmaxc(4.17)
盲区 R B R_B RB 位于:
R B = c ∗ k 2 f s , k = 0 , 1 , 2 , … R_B=\frac{c * k}{2 f_s}, \quad k=0,1,2, \ldots RB=2fsc∗k,k=0,1,2,…(4.18)
FMCIW用于自动巡航控制(ACC)雷达,这是因为这些雷达传统上使用FMCW波形,这对于减少近距离杂波和最大限度地提高远程探测具有重要意义。
4.6 快速chirp斜坡序列波形(核心内容)
虽然FMCW是汽车雷达和其他应用中广泛使用的波形,但其主要缺点是在多目标环境中,需要对每个目标的速度和距离进行耦合,这被称为解耦合。
不正确的解耦合可会导致目标位置或速度估计错误,为了避免这个问题,图8所示的快速chirp(啁啾)斜坡序列使得不需要解耦合就可以估计目标距离和速度。
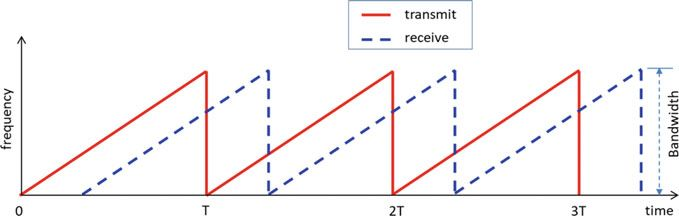
(图8 用于距离和速度检测的快速啁啾斜坡序列波形示例)
距离和速度的获取过程采用2-DFT,首先对每一个啁啾斜坡进行一次DFT获取距离信息,然后再进行一次DFT获得速度信息,还可以根据接收啁啾斜坡序列的天线结构进一步计算角度信息,就可以构建三维目标数据,包括距离、速度和角度。
对于角度估计,可以使用Capon、MUSIC和ESPRIT等高分辨率算法。如图9所示,沿着啁啾采样点进行DFT可以得到每个啁啾的距离,而沿着DFT进行FFT可以得到速度。 此外,通过使用例如MUSIC独立计算角度,可以得出到达方向估计值。 最后,结果是3D数据立方体,由每个检测到的目标的距离、速度和到达角组成。
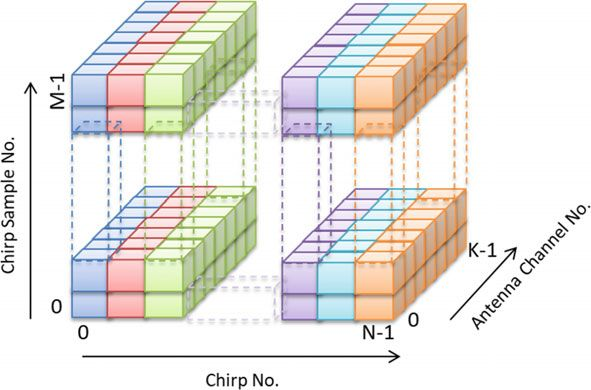
(图9 基于啁啾斜坡序列波形的三维数据立方体概念示意图)
如果快速啁啾斜坡序列从载波频率 f c f_c fc 扫过,即起始频率为 f c f_c fc,则任何给定时刻 f ( t ) f(t) f(t) 的频率可以表示为:
f ( t ) = f c + B T t = f c + α t f(t)=f_c+\frac{B}{T} t=f_c+\alpha t f(t)=fc+TBt=fc+αt(4.19)
其中, B B B 为扫描带宽, T T T 为扫描持续时间, α = B / T \alpha=B / T α=B/T 为调频斜率,如图8所示。由关系式可以得到对应的瞬时相位:
ω ( t ) = d φ ( t ) d t = 2 π f ( t ) \omega(t)=\frac{d \varphi(t)}{\mathrm{d} t}=2 \pi f(t) ω(t)=dtdφ(t)=2πf(t)(4.20)
其中, φ ( t ) = ∫ 0 t 2 π f ( t ) d t = 2 π ( f c t + α 2 t 2 ) + φ 0 , φ 0 \varphi(t)=\int_0^t 2 \pi f(t) \mathrm{d} t=2 \pi\left(f_c t+\frac{\alpha}{2} t^2\right)+\varphi_0, \varphi_0 φ(t)=∫0t2πf(t)dt=2π(fct+2αt2)+φ0,φ0 代表初始相位。
故而,发射信号可以表示为:
s ( t ) = A cos ( 2 π ( f c t + α 2 t 2 ) + φ 0 ) s(t)=A \cos \left(2 \pi\left(f_c t+\frac{\alpha}{2} t^2\right)+\varphi_0\right) s(t)=Acos(2π(fct+2αt2)+φ0)(4.21)
在不考虑初始相位的情况下,发射的第 m m m 个chirp的一般表达式如下:
s ( t ) = A cos ( 2 π f c t + π α 2 ( t − m T ) 2 ) s(t)=A \cos \left(2 \pi f_c t+\frac{\pi \alpha}{2}(t-m T)^2\right) s(t)=Acos(2πfct+2πα(t−mT)2)(4.22)
对于距离为R,距离雷达径向速度为 v v v 的目标,反射chirp信号的往返延迟时间 τ \tau τ 为:
τ = 2 ( R + v t ) c \tau=\frac{2(R+v t)}{c} τ=c2(R+vt)(4.23)
接收到的 r ( t ) r(t) r(t) 延迟chirp信号变为:
r ( t ) = B cos ( 2 π f c ( t − τ ) + π α 2 ( t − τ − m T ) 2 ) r(t)=B \cos \left(2 \pi f_c(t-\tau)+\frac{\pi \alpha}{2}(t-\tau-m T)^2\right) r(t)=Bcos(2πfc(t−τ)+2πα(t−τ−mT)2)(4.24)
假设发射和接收的啁啾信号的振幅 A A A 归一化,我们得到:
s
(
t
)
=
cos
(
2
π
f
c
t
+
π
α
2
(
t
−
m
T
)
2
)
s(t)=\cos \left(2 \pi f_c t+\frac{\pi \alpha}{2}(t-m T)^2\right)
s(t)=cos(2πfct+2πα(t−mT)2)
r
(
t
)
=
cos
(
2
π
f
c
(
t
−
τ
)
+
π
α
2
(
t
−
τ
−
m
T
)
2
)
r(t)=\cos \left(2 \pi f_c(t-\tau)+\frac{\pi \alpha}{2}(t-\tau-m T)^2\right)
r(t)=cos(2πfc(t−τ)+2πα(t−τ−mT)2)(4.25)
将发射信号和接收信号通过混频器和低通滤波器,得到g(t)表示为
g
(
t
)
=
s
(
t
)
r
(
t
)
=
cos
(
2
π
f
c
t
+
π
α
2
(
t
−
m
T
)
2
)
cos
g(t)=s(t) r(t)=\cos \left(2 \pi f_c t+\frac{\pi \alpha}{2}(t-m T)^2\right) \cos
g(t)=s(t)r(t)=cos(2πfct+2πα(t−mT)2)cos
(
2
π
f
c
(
t
−
τ
)
+
π
α
2
(
t
−
τ
−
m
T
)
2
)
\left(2 \pi f_c(t-\tau)+\frac{\pi \alpha}{2}(t-\tau-m T)^2\right)
(2πfc(t−τ)+2πα(t−τ−mT)2)(4.26)
用三角恒等式 cos ( x ) cos ( y ) = 1 / 2 ( cos ( x + y ) + cos ( x − y ) ) \cos (x) \cos (y)=1 / 2(\cos (x+y)+\cos (x-y)) cos(x)cos(y)=1/2(cos(x+y)+cos(x−y)) ,高频分量 S S S 经过低通滤波器过滤,我们得到:
g ( t ) ≅ 1 2 cos ( 2 π f c τ + 2 π α τ ( t − m T ) − π α τ 2 ) g(t) \cong \frac{1}{2} \cos \left(2 \pi f_c \tau+2 \pi \alpha \tau(t-m T)-\pi \alpha \tau^2\right) g(t)≅21cos(2πfcτ+2πατ(t−mT)−πατ2)(4.27)
将 τ \tau τ 代入得到:
g ( t ) = 1 2 cos ( 2 π f c ( 2 ( R + v t ) c ) + 2 π α ( 2 ( R + v t ) ( t − m T ) c ) − π α ( 2 ( R + v t ) c ) 2 ) g(t)=\frac{1}{2} \cos \left(2 \pi f_c\left(\frac{2(R+v t)}{c}\right)+2 \pi \alpha\left(\frac{2(R+v t)(t-m T)}{c}\right)-\pi \alpha\left(\frac{2(R+v t)}{c}\right)^2\right) g(t)=21cos(2πfc(c2(R+vt))+2πα(c2(R+vt)(t−mT))−πα(c2(R+vt))2)(4.28)
因为 c 2 ≫ ( R + v t ) 2 c^2 \gg(R+v t)^2 c2≫(R+vt)2 ,所以第三项可以忽略不计,则混频器和低通滤波器输出结果为:
g
(
t
)
=
1
2
cos
(
2
π
f
c
(
2
(
R
+
v
t
)
c
)
+
2
π
α
(
2
(
R
+
v
t
)
(
t
−
m
T
)
c
)
)
g(t)=\frac{1}{2} \cos \left(2 \pi f_c\left(\frac{2(R+v t)}{c}\right)+2 \pi \alpha\left(\frac{2(R+v t)(t-m T)}{c}\right)\right)
g(t)=21cos(2πfc(c2(R+vt))+2πα(c2(R+vt)(t−mT)))
g
(
t
)
=
1
2
cos
(
2
π
(
2
R
f
c
c
+
2
f
c
v
t
c
)
+
2
π
α
(
2
(
R
t
−
R
m
T
+
v
t
2
−
m
v
t
T
)
c
)
)
g(t)=\frac{1}{2} \cos \left(2 \pi\left(\frac{2 R f_c}{c}+\frac{2 f_c v t}{c}\right)+2 \pi \alpha\left(\frac{2\left(R t-R m T+v t^2-m v t T\right)}{c}\right)\right)
g(t)=21cos(2π(c2Rfc+c2fcvt)+2πα(c2(Rt−RmT+vt2−mvtT)))
g
(
t
)
=
1
2
cos
(
2
π
(
2
R
f
c
c
+
2
f
c
v
t
c
+
(
2
R
α
t
−
2
R
α
m
T
+
2
α
v
t
2
−
2
m
α
v
t
T
)
c
)
)
g(t)=\frac{1}{2} \cos \left(2 \pi\left(\frac{2 R f_c}{c}+\frac{2 f_c v t}{c}+\frac{\left(2 R \alpha t-2 R \alpha m T+2 \alpha v t^2-2 m \alpha v t T\right)}{c}\right)\right)
g(t)=21cos(2π(c2Rfc+c2fcvt+c(2Rαt−2RαmT+2αvt2−2mαvtT)))(4.29)
考虑到 t s t_s ts 是从第 m m m 个chirp开始的时间,我们可以写为:
t = t s + m T , 0 ≤ t 0 ≤ T t=t_s+m T, 0 \leq t_0 \leq T t=ts+mT,0≤t0≤T(4.30)
将上述表达式 (4.30) 代入 g ( t ) g(t) g(t) 得到:
g ( t s ) = 1 2 cos ( 2 π ( 2 R f c c + 2 f c v ( t s + m T ) c + ( 2 R α ( t s + m T ) − 2 R α m T + 2 α v ( t s + m T ) 2 − 2 m α v ( t s + m T ) T ) c ) ) ) g ( t s ) = 1 2 cos ( 2 π ( 2 R f c c + 2 f c v ( t s + m T ) c + ( 2 R α ( t s + m T ) − 2 R α m T + 2 α v ( t s 2 + 2 m t s T + m 2 T 2 ) − 2 m α v ( t s + m T ) T ) c ) ) \begin{aligned} g\left(t_s\right)=& \frac{1}{2} \cos \left(2 \pi\left(\frac{2 R f_c}{c}+\frac{2 f_c v\left(t_s+m T\right)}{c}\right.\right.\\ &\left.\left.\left.+\frac{\left(2 R \alpha\left(t_s+m T\right)-2 R \alpha m T+2 \alpha v\left(t_s+m T\right)^2-2 m \alpha v\left(t_s+m T\right) T\right)}{c}\right)\right)\right) \\ g\left(t_s\right)=& \frac{1}{2} \cos \left(2 \pi\left(\frac{2 R f_c}{c}+\frac{2 f_c v\left(t_s+m T\right)}{c}\right.\right.\\ &\left.\left.+\frac{\left(2 R \alpha\left(t_s+m T\right)-2 R \alpha m T+2 \alpha v\left(t_s^2+2 m t_s T+m^2 T^2\right)-2 m \alpha v\left(t_s+m T\right) T\right)}{c}\right)\right) \end{aligned} g(ts)=g(ts)=21cos(2π(c2Rfc+c2fcv(ts+mT)+c(2Rα(ts+mT)−2RαmT+2αv(ts+mT)2−2mαv(ts+mT)T)⎠ ⎞⎠ ⎞⎠ ⎞21cos(2π(c2Rfc+c2fcv(ts+mT)+c(2Rα(ts+mT)−2RαmT+2αv(ts2+2mtsT+m2T2)−2mαv(ts+mT)T)))(4.31)
通过假设二阶项可以忽略不计, g ( t s ) g\left(t_s\right) g(ts) 可以近似为:
g ( t s ) = 1 2 cos ( 2 π ( 2 R f c c + 2 v m T f c c + ( 2 R α + 2 v f c + 2 m B v ) t s c ) ) g\left(t_s\right)=\frac{1}{2} \cos \left(2 \pi\left(\frac{2 R f_c}{c}+\frac{2 v m T f_c}{c}+\frac{\left(2 R \alpha+2 v f_c+2 m B v\right) t_s}{c}\right)\right) g(ts)=21cos(2π(c2Rfc+c2vmTfc+c(2Rα+2vfc+2mBv)ts))(4.32)
其中, B = α T B=\alpha T B=αT 。 假设目标缓慢移动并且第一项对应于恒定相位, g ( t s ) g\left(t_s\right) g(ts) 可简洁地表示为:
g ( t s ) = 1 2 cos ( 2 π ( m T f d + f p k t s ) ) g\left(t_s\right)=\frac{1}{2} \cos \left(2 \pi\left(m T f_d+f_{p k} t_s\right)\right) g(ts)=21cos(2π(mTfd+fpkts))(4.33)
其中, f p k = ( 2 R α + 2 v f c + 2 m B v ) c = ( 2 R α ) c + f d + ( 2 m B v ) c = f beat + f d + f m . \begin{aligned} f_{p k} &=\frac{\left(2 R \alpha+2 v f_c+2 m B v\right)}{c}=\frac{(2 R \alpha)}{c}+f_d+\frac{(2 m B v)}{c} \\ &=f_{\text {beat }}+f_d+f_m . \end{aligned} fpk=c(2Rα+2vfc+2mBv)=c(2Rα)+fd+c(2mBv)=fbeat +fd+fm. 。
f beat f_{\text {beat }} fbeat 是由发射和接收信号之间的时间延迟引入的拍频, f m f_m fm 是在扫描期间由于目标运动而产生的频率分量,通常被认为可以忽略不计。 对于快速chirp斜坡,斜坡之间的多普勒频移通常被认为可以忽略不计。 因此距离可以从拍频表示为:
f beat = ( 2 R α ) c R = c f beat 2 α \begin{aligned} f_{\text {beat }} &=\frac{(2 R \alpha)}{c} \\ R &=\frac{c f_{\text {beat }}}{2 \alpha} \end{aligned} fbeat R=c(2Rα)=2αcfbeat (4.34)
通过考虑 f d + f m f_d+f_m fd+fm分量可以提高距离精度,距离是通过对拍频信号 g ( t s ) g\left(t_s\right) g(ts) 进行 FFT 来计算的,其中每个chirp的频率峰值近似对应于 f beat f_{\text {beat }} fbeat 。
利用时移性质, g ( t s ) g\left(t_s\right) g(ts) 的傅里叶变换由下式给出:
G ( f ) = 1 4 ( e i 2 π m T f d ) δ ( f − f beat ) + 1 4 ( e − i 2 π m T f d ) δ ( f + f beat ) G(f)=\frac{1}{4}\left(\mathrm{e}^{i 2 \pi m T f_d}\right) \delta\left(f-f_{\text {beat }}\right)+\frac{1}{4}\left(\mathrm{e}^{-i 2 \pi m T f_d}\right) \delta\left(f+f_{\text {beat }}\right) G(f)=41(ei2πmTfd)δ(f−fbeat )+41(e−i2πmTfd)δ(f+fbeat )(4.35)
4.6.1 距离分辨率和最大探测距离
距离分辨率只与chirp的带宽B有关,可以表示为:
Δ R = c 2 B \Delta R=\frac{c}{2 B} ΔR=2Bc(4.36)
如果用 N N N(2的幂次)个实数点来计算FFT,那么可以计算的最大距离为:
R max = ( N 2 ) ∗ Δ R = c N 4 B R_{\max }=\left(\frac{N}{2}\right) * \Delta R=\frac{c N}{4 B} Rmax=(2N)∗ΔR=4BcN(4.37)
然而,绝对最大距离取决于chirp,由 c T / 2 c T / 2 cT/2 决定,与 FFT 样本无关。
例如,给定 4 GHz 的扫描带宽 B W B W BW ,可实现的距离分辨率可计算如下:
Δ
R
=
c
2
B
=
3
×
1
0
8
2
×
4
×
1
0
9
=
0.0375
[
m
]
\Delta R=\frac{c}{2 B}=\frac{3 \times 10^8}{2 \times 4 \times 10^9}=0.0375[\mathrm{~m}]
ΔR=2Bc=2×4×1093×108=0.0375[ m]
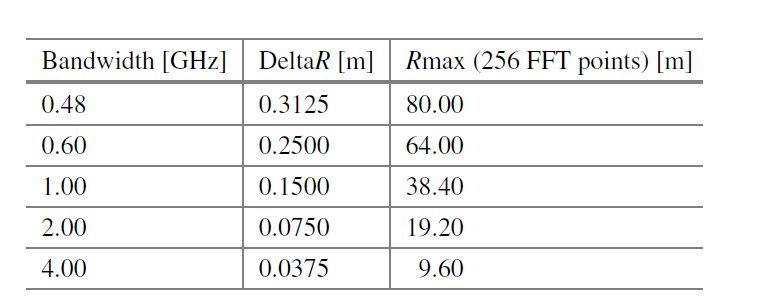
(表 4.1 给出了典型的 BW 值和相应的距离分辨率值)
4.6.2 速度分辨率和最大速度
根据奈奎斯特定理,最大多普勒频率取决于chirp周期T,由下式给出:
f d max = 1 2 T f_{d \max }=\frac{1}{2 T} fdmax=2T1(3.38)
从多普勒频率的定义出发,给出了相应的最大速度:
f
d
max
=
1
2
T
=
2
f
c
v
max
c
f_{d \max }=\frac{1}{2 T}=\frac{2 f_c v \max }{c}
fdmax=2T1=c2fcvmax
(4.39)
其中,
v
max
=
c
2
T
∗
2
f
c
=
c
4
f
c
T
v_{\max }=\frac{c}{2 T * 2 f_c}=\frac{c}{4 f_c T}
vmax=2T∗2fcc=4fcTc 。
如果单次扫描总共有 M M M 个chirp,则多普勒分辨率为 f d = 1 / M T f_d=1 / M T fd=1/MT ,则速度分辨率 v v v 由下式给出:
Δ v = Δ v = c 2 f c ∗ 1 M T = c 2 f c M T \Delta v=\Delta v=\frac{c}{2 f_c} * \frac{1}{M T}=\frac{c}{2 f_c M T} Δv=Δv=2fcc∗MT1=2fcMTc(4.40)
增加chirp的数量可以提高速度分辨率,假设单次扫描产生64个chirp,中心频率79 GHz,速 40 μ s 40 \mu s 40μs 的chirp周期分辨率为:
Δ v = 3 × 1 0 8 2 ∗ 79 × 1 0 9 ∗ 64 ∗ 40 × 1 0 − 6 = 2.23 [ m s ] \Delta v=\frac{3 \times 10^8}{2 * 79 \times 10^9 * 64 * 40 \times 10^{-6}}=2.23\left[\frac{\mathrm{m}}{\mathrm{s}}\right] Δv=2∗79×109∗64∗40×10−63×108=2.23[sm]























 3457
3457











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










