三维视觉之数字图像处理基础（五） 图像几何变换

图像几何变换

1 图像几何变换模型

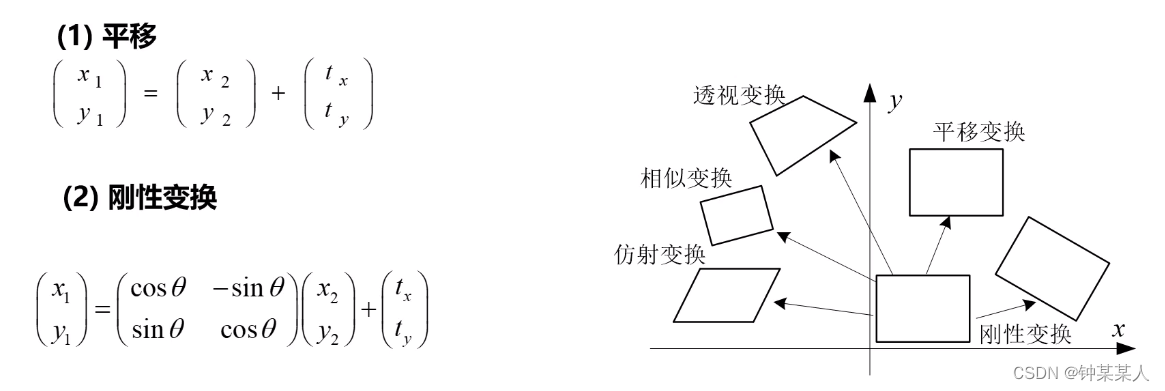
刚性变换有三个参数：旋转角度θ、平移向量（tx，ty），刚性变换不改变图像内部结构的长度和角度。



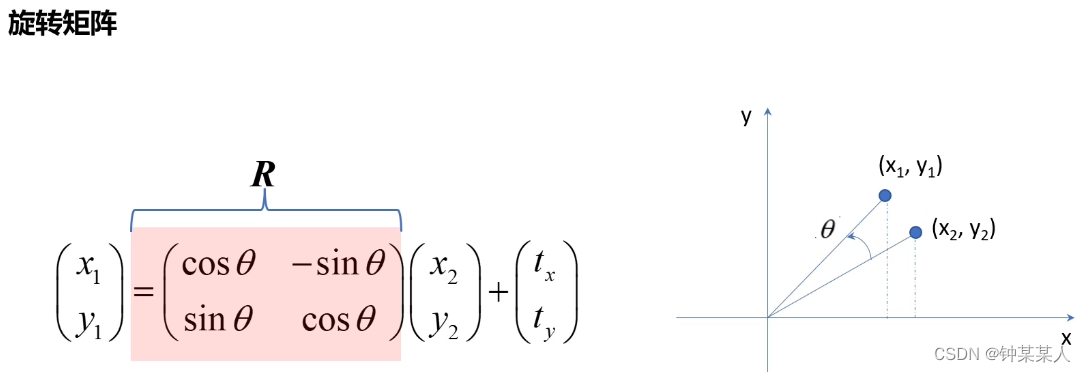
相似变换有四个参数：旋转角度θ、平移向量（tx，ty）、尺度变换参数s。相当于图像的旋转平移缩放变换组合。

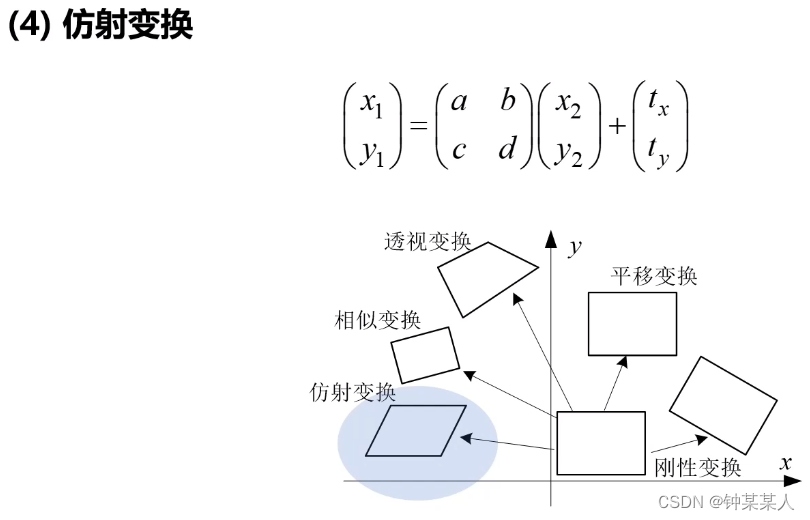
仿射变换有六个参数：线性变换参数abcd，平移向量（tx，ty）。会改变目标结构的长度，也会改变角度，但是原有结构里面平行关系的结构会的到保持，例如上图平行四边形，平行的边依然保持平行。

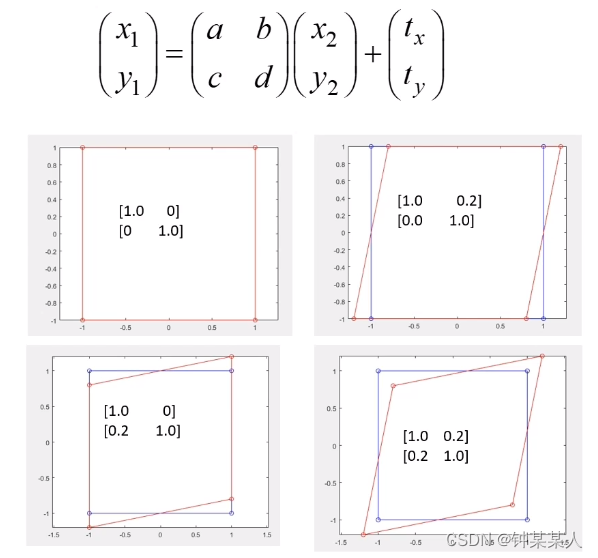
仿射变换参数求解：

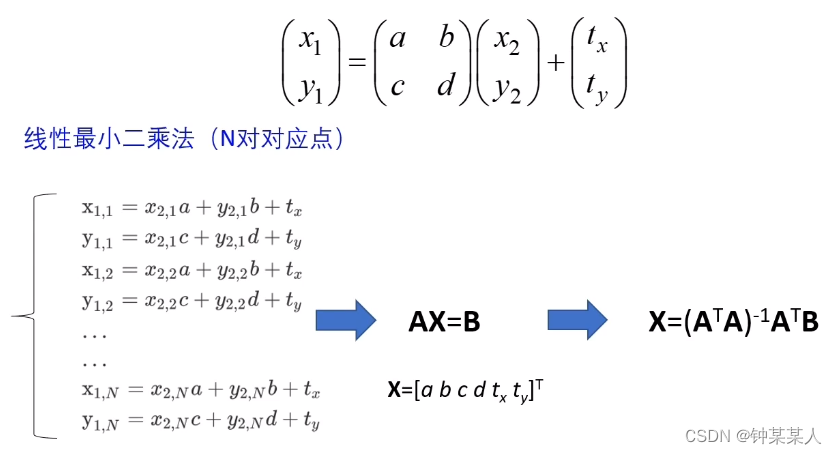
例子：

投影变换（透视变换）：有8个自由度，经常应用于图像拼接，用相机拍摄后的图片就存在透视变换。

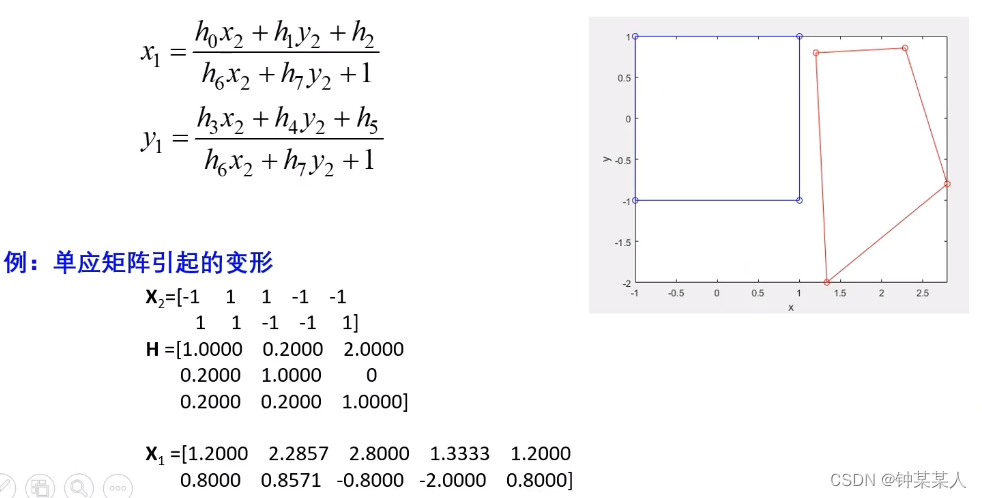
2 图像插值

为什么需要图像插值？：图像旋转或者缩放之后，对于坐标位置(x,y),x、y不是整数，如何获取(x,y)处的图像灰度值？

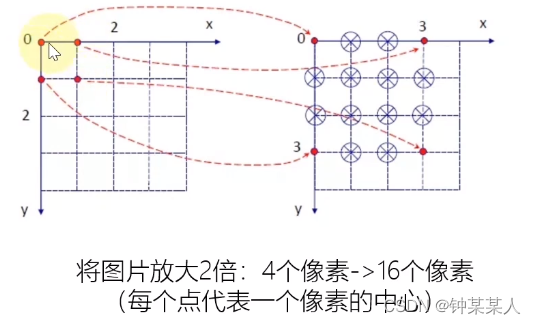
2.1 一维线性插值

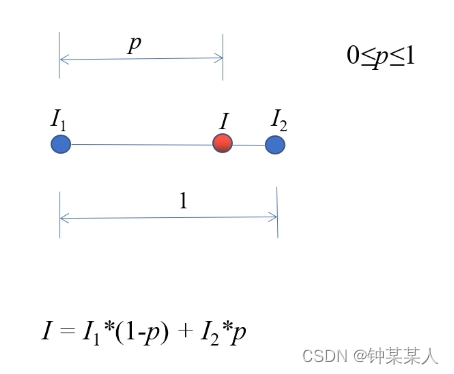
2.2 双线性插值

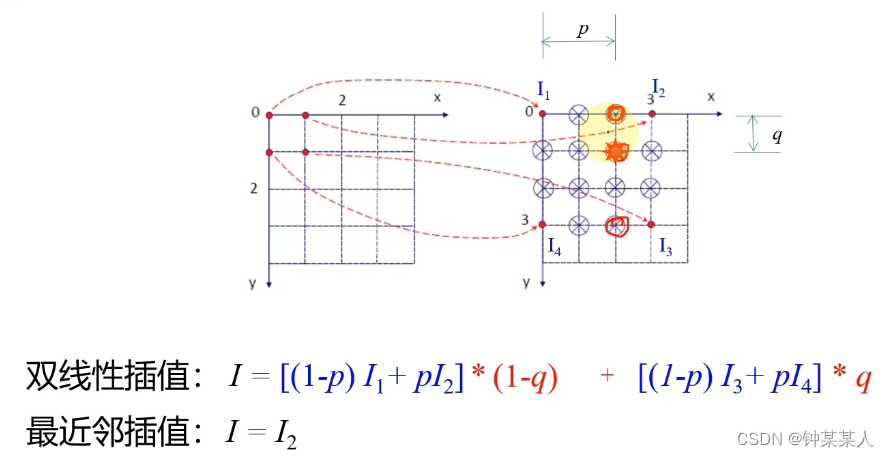
在水平和竖直方向做两次线性插值。

上图，从左向右为：6464像素的图像、最近邻差值后512512像素的图像、双线性插值512*512像素的图像

3 应用举例

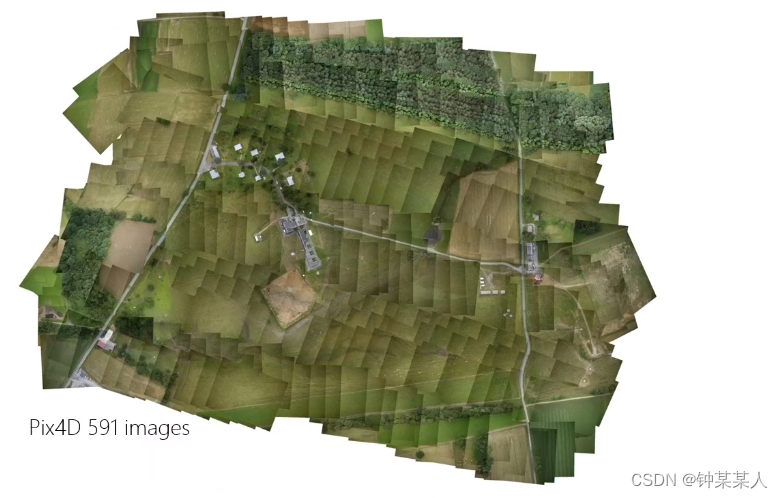
3.1 无人机图像拼接

图像拼接可以将无人机获得的多张图像拼接成视场更大的图像，以获得更好的整体感知效果。随着待拼接的图像数量的增加，普通的基于两两配准的图像拼接方法得到的拼接结果变形会越来越严重（几何配准的累计误差、场景非平面等因素）。
为了得到好的拼接结果，通常需要引入GPS/IMU、GCP等信息获取相机姿态；或者利用卫星图像作为基准图像，把拼接图像与参考图像配准后，叠加在参考图像上。
如果这些信息都不可用，对于成百上千的待拼接图像，如何获得良好的拼接结果？


图像变换为投影变换，拼接目标函数的数据项表示配准的特征点之间的距离（越小越好）；正则项为了保持图像变换尽量为刚性变换的模型，所以g和h要尽量为0，这样abcd趋向一个刚性变换(整个变换矩阵趋向于一个旋转矩阵)，由旋转矩阵可得：正则项的前三项表示相互正交且模为1。

拼接流程：

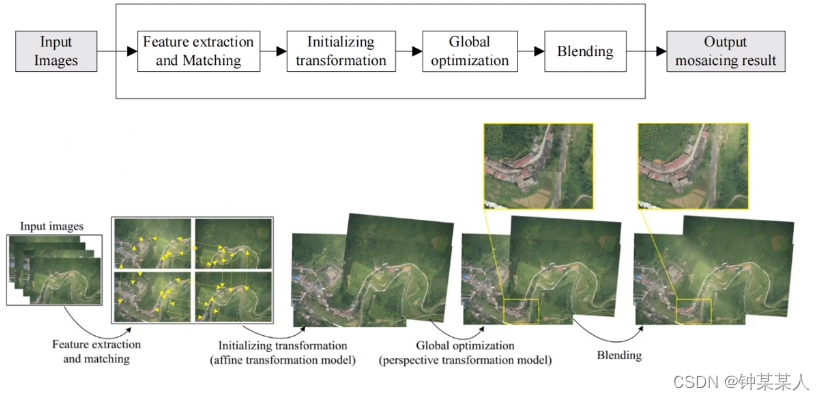
1、对多幅输入的图像进行特征提取和匹配，上图用到sift特征提取。
2、初始化特征变换，初始化为了效率，采用仿射变形参数
3、全局优化，
4、特征融合，消除拼接缝

随机采样一致性算法（RANSAC）
模型参数拟合时，数据中经常会有噪声。

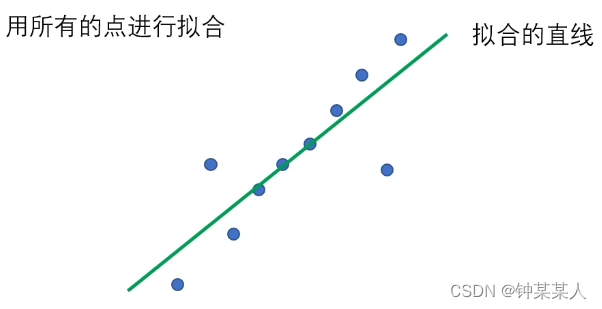
RANSAC算法思想：



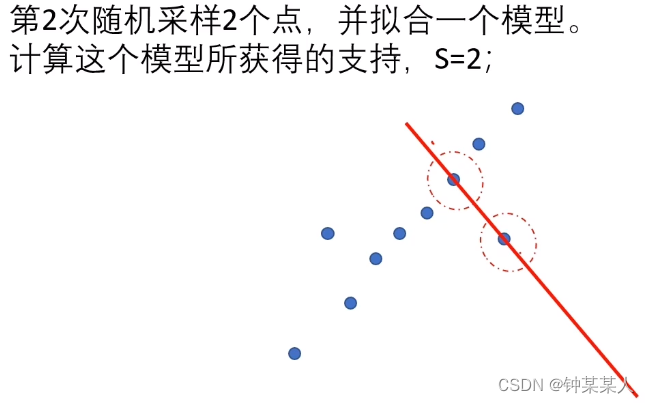
进行K次采样，根据模型获得的支持度参数，将点进行分类：

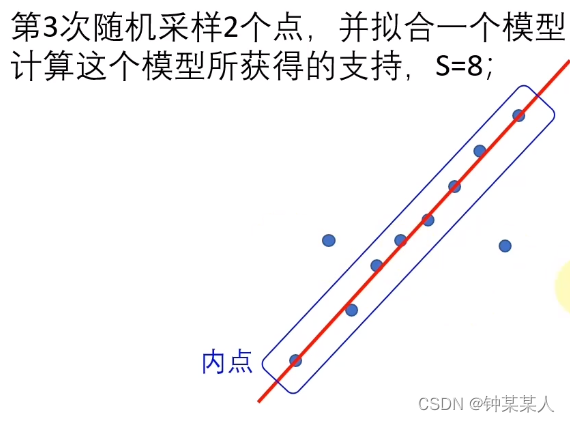
此时的模型，获得了最大的支持度，支持这个模型的点称为“内点”。用所有的内点，重新拟合一个参数，作为最终的拟合参数。

RANSAC算法是一个鲁棒的参数拟合算法