交叉数为6和7的纽结曲线方程

几千年来，人类一直在打结。但是什么是数学结呢？从一根不计粗细的绳子开始，在上面打一个结，然后粘在末端形成一个打结的环，就是一个数学的结。

为什么要研究这样的结呢？在19世纪末，科学家们正试图为原子建立一个模型。为了解释不同类型的元素，开尔文勋爵假设原子只是乙醚中打结的旋涡。例如平凡结或、三叶结和8字结可以分别代表氢、碳和氧元素。

虽然与今天使用的玻尔原子模型相比，这似乎是一个奇特的概念，但开尔文勋爵有几个理由相信这些打结的涡旋可以描述物质的原子结构。首先，流体中的涡旋非常稳定，所以每个结都可以根据其几何性质进行分类。第二，有无穷无尽的结可以用来表示各种化学元素。最后，就像烟雾环振动一样，醚涡管的振荡可能产生原子谱线，可以用来识别原子和分子。

由于结可能代表这些元素的概念，科学家们开始创建不同结的图表，认为从某种意义上说，它们是在创建一个元素周期表。这项工作在很大程度上被与开尔文勋爵同时代的人，苏格兰物理学家泰特所采纳，他在1877年发表了一系列关于纽结枚举的论文中的第一篇。在其他人的帮助下，包括美国数学家利特，到20本世纪末，所有多达10个交叉点的列举几乎完成了。知道玻尔原子模型的出现，理论物理学家逐渐对结失去了兴趣。

但幸运的是纽结引起的数学的兴趣，且生化学家在细菌中发现了打结的DNA分子；最近的研究也探讨了在蛋白质链中打结的重要性；分子化学家已经创造出了可打结的新分子化合物。因此，从19世纪末开始的一个科学错误已经变成了一个重要的数学研究领域，在化学和生物学中有着重要的应用。

纽结理论中确定两个结是否相等可能具有挑战性。雷德迈斯特、亚历山大和布里格斯的一个重要定理是，当且仅当一个结的投影可以通过三种局部图解序列投影到另一个结的投影时，两个结是等价的。虽然雷德梅斯特移动提供了一种方法来确定两个结是否是等价的，给定两个等价的结，没有已知的算法提供雷德梅斯特移动的序列，需要将一个结的投影转换为另一个结的投影。或者给定两个非等价的结，没有一般的方法来使用雷德梅斯特移动来显示这两个结是不同的。为了帮助确定两个结是否等价，我们转向不同的结不变量。结不变量是一种将结的每个表示、某个代数对象——一个数字，一个多项式——关联起来的方法，使这个对象在雷德梅斯特移动下保持不变。

在此基础上，纽结理论中对10个交叉点以下的纽结进行了命名，并制作了各种纽结列表。以下是纽结表中部分纽结三维曲线的方程，可以方便对纽结建模以及各种纽结不变量的计算。

6-1

x(t) = 12*cos(t) + 20*sin(t) - 163*cos(2*t) + 76*sin(2*t) - 87*cos(3*t) - 15*sin(3*t) - 21*cos(4*t) + 14*sin(4*t) + 24*cos(5*t) - 50*sin(5*t)

y(t) = 29*cos(t) + 78*sin(t) - 180*cos(2*t) + 58*sin(2*t) + 88*cos(3*t) + 72*sin(3*t) - 14*sin(4*t)

z(t) = - 30*cos(t) - 78*sin(t) - 111*cos(2*t) + 37*sin(2*t) - 67*cos(3*t) - 51*sin(3*t) + 31*cos(4*t) + 8*sin(4*t) -11*cos(5*t) + 65*sin(5*t)

% 6-1
clc,clear,close all
t=linspace(0,2*pi,1000);
x= 12*cos(t) + 20*sin(t) - 163*cos(2*t) + 76*sin(2*t) - 87*cos(3*t) - 15*sin(3*t) - 21*cos(4*t) + 14*sin(4*t) + 24*cos(5*t) - 50*sin(5*t);
y= 29*cos(t) + 78*sin(t) - 180*cos(2*t) + 58*sin(2*t) + 88*cos(3*t) + 72*sin(3*t) - 14*sin(4*t);
z= - 30*cos(t) - 78*sin(t) - 111*cos(2*t) + 37*sin(2*t) - 67*cos(3*t) - 51*sin(3*t) + 31*cos(4*t) + 8*sin(4*t) -11*cos(5*t) + 65*sin(5*t);
%plot3(x,y,z)
P=[x' y' z'];DrawMutiCylinder(P,40,10,40,10,linspace(0,1,1000)')

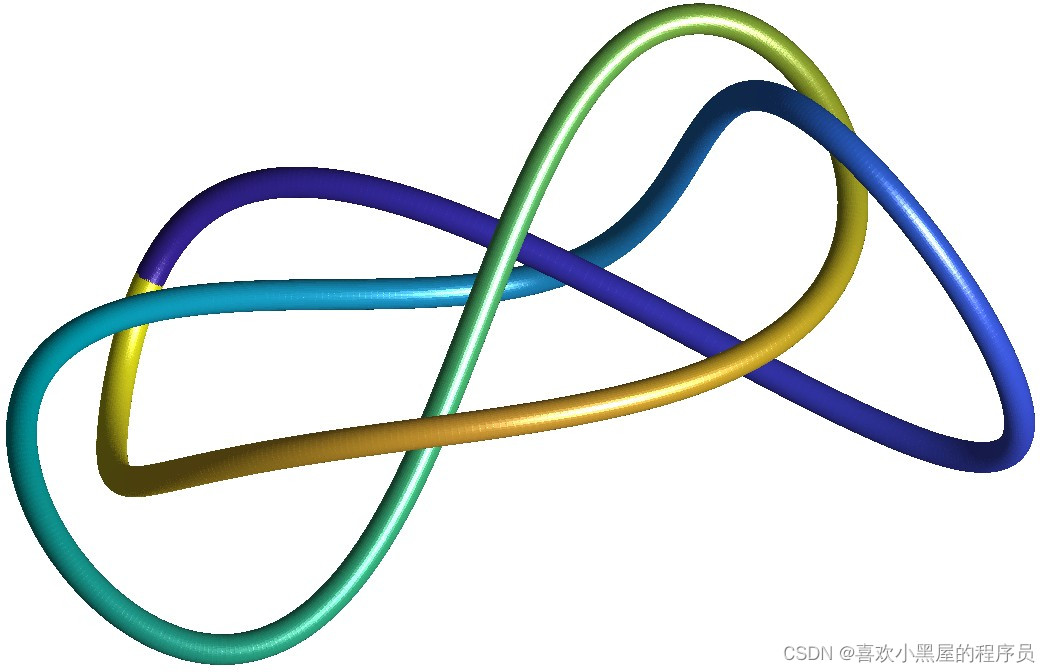
6-2

x(t) = - 6*cos(t) - 21*sin(t) - 195*cos(2*t) + 92*sin(2*t) - 64*cos(3*t) - 23*sin(3*t) - 6*cos(4*t) + 13*sin(4*t) +24*cos(5*t) + 15*sin(5*t) + 41*sin(6*t)

y(t) = - 21*cos(t) - 24*sin(t) - 207*cos(2*t) - 72*sin(2*t) + 112*cos(3*t) - 7*sin(3*t) - 13*cos(4*t) - 40*sin(4*t) -27*cos(5*t) - 3*sin(5*t) - 17*cos(6*t)

z(t) = - 18*cos(t) - 13*sin(t) + 113*cos(2*t) - 107*sin(2*t) + 86*cos(3*t) - 9*sin(3*t) - 26*cos(4*t) - 7*sin(4*t) +24*cos(5*t) + 33*sin(5*t) + 21*cos(6*t) + 31*sin(6*t)

clc,clear
t=linspace(0,2*pi,1000);
x= - 6*cos(t) - 21*sin(t) - 195*cos(2*t) + 92*sin(2*t) - 64*cos(3*t) - 23*sin(3*t) - 6*cos(4*t) + 13*sin(4*t) +24*cos(5*t) + 15*sin(5*t) + 41*sin(6*t);
y= - 21*cos(t) - 24*sin(t) - 207*cos(2*t) - 72*sin(2*t) +