从零开始的深度学习（二）：各类卷积变种介绍

分组卷积

概念

原始卷积操作中每一个输出通道都与输入的每一个通道相连接，通道之间是以稠密方式进行连接。而组卷积中输入和输出的通道会被划分为多个组，每个组的输出通道只和对应组内的输入通道相连接，而与其它组的通道无关。这种分组(split)的思想随后被绝大多数的新晋卷积所应用。

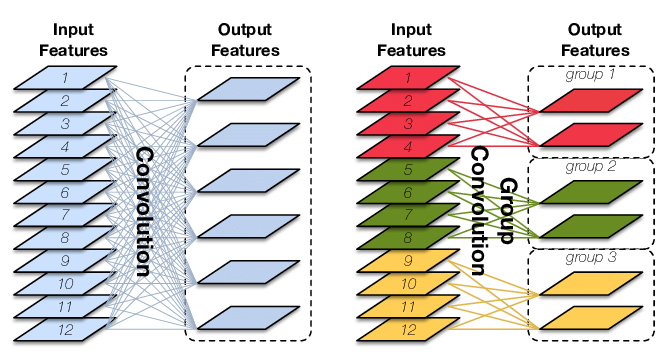
将输入特征图按通道均分为g组，然后对每一组进行常规卷积；

由于分组后，每组特征图的通道数为$\frac{C_{in}}{g}$，所以每个卷积核的通道数也降低到$\frac{C_{in}}{g}$；

由于每组内进行的是常规卷积，所以每组至少需要一个卷积核，即分组卷积输出通道数至少为g，如果每组有n个卷积核，则输出$C_{out}=n\times g,n\ge 1$，所以输出通道数是分组数的整数倍；

综上所述，分组卷积中要求输入和输出通道数均能整除分组数 g。

分组卷积的运算量和参数量的减少，归根结底是一个卷积核本身通道数减少为原来的 g 分之一。

整个分组卷积的参数量：
$$Params=\{\begin{array}{rlr}& C_{out}\times (\frac{C_{in}}{g}\times K_1\times K_2),& bias=False\\ & C_{out}\times (\frac{C_{in}}{g}\times K_1\times K_2+1),& bias=True\end{array}$$

作用

• 减少运算量和参数量，相同输入输出大小的情况下，减少为原来的$\frac{1}{g}$。

• 隔绝不同组的信息交换。

• • 在某些情况下，如每个输出与输入的一部分特征图相关联时，分组卷积可以取得比常规卷积更好的性能，如输出通道为2，它们分别只与输入的1，2和3，4通道相关，这时最好使用g=2的分组卷积，相当于直接让模型将不相关的输入通道权重设置为零，加快模型收敛。
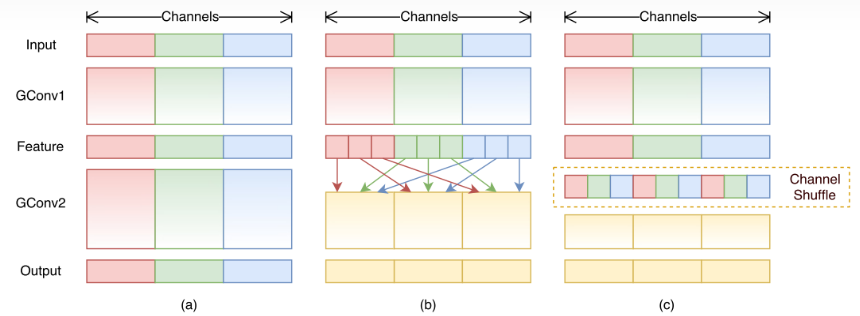
  • 但对于需要考虑所有输入特征图信息的情况，分组卷积会降低模型的性能，对于这个问题，常常在两个分组卷积之间加入Channel_Shuffle模块打乱通道顺序，从而实现不同分组间的信息交换。

转置卷积（反卷积）

基础概念

转置卷积，也称为反卷积(Deconvolution)，一般应用在编解码结构中的解码器部分或者DCGAN中的生成器中等。从数学计算上看，“反卷积”相当于是将卷积核转换为稀疏矩阵后进行转置计算，因此，也被称为“转置卷积”。但由于数字信号处理中也有反卷积的概念，所以一般为了不造成歧义，大多数框架的API都会定义为转置卷积。转置卷积是一种特殊的正向卷积，先按照一定的比例通过补 0 来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

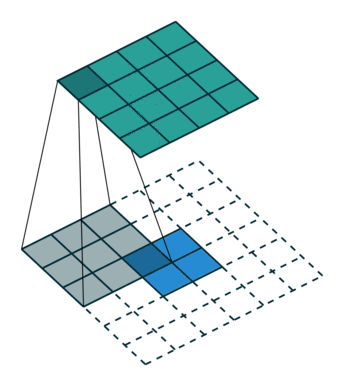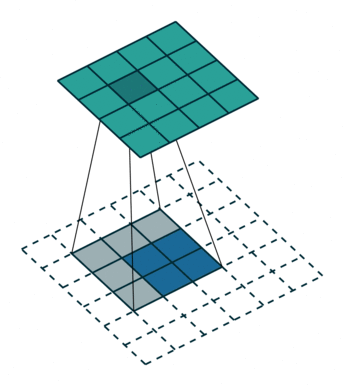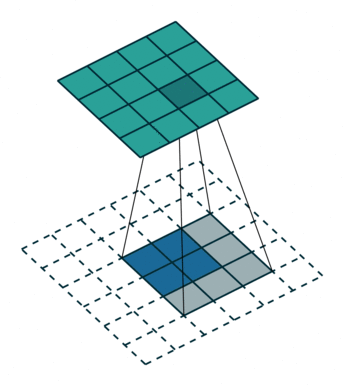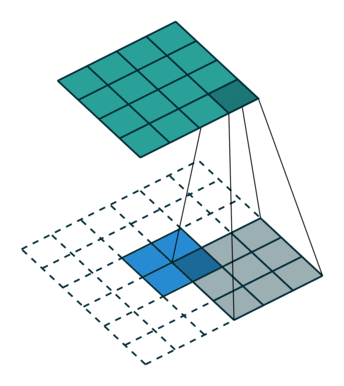
如下图，在2x2的输入图像上应用步长为1、边界全0填充的3x3卷积核，进行转置卷积（反卷积）计算，向上采样后输出的图像大小为4x4。

原理推导

对于一个输入大小为$3\times 3$的图像，卷积核大小为$2\times 2$：
$$X=\left[\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& x_{22}& x_{23}\\ x_{31}& x_{32}& x_{33}\end{array}\right]$$

$$W=\left[\begin{array}{cc}{w}_{11}& w_{12}\\ w_{21}& w_{22}\end{array}\right]$$

计算输出$Y$的具体实现方法为矩阵乘法。

将卷积核表示为稀疏矩阵C：
$$C=\left[\begin{array}{ccccccccc}{w}_{11}& w_{12}& 0& w_{21}& w_{22}& 0& 0& 0& 0\\ 0& w_{11}& w_{12}& 0& w_{21}& w_{22}& 0& 0& 0\\ 0& 0& 0& w_{11}& w_{12}& 0& w_{21}& w_{22}& 0\\ 0& 0& 0& 0& w_{11}& w_{12}& 0& w_{21}& w_{22}\end{array}\right]$$
每一行向量表示在一个位置的卷积操作，0填充表示卷积核未覆盖到的区域。

将输入$X$ 展开为列向量：
$$x={\left[\begin{array}{ccccccccc}{x}_{11}& x_{12}& x_{13}& x_{21}& x_{22}& x_{23}& x_{31}& x_{32}& x_{33}\end{array}\right]}^T$$
则卷积操作可以表示为：
$$y=Cx$$
输出向量$y$的大小为$4\times 1$的列向量，改写为矩阵即为$2\times 2$。

转置卷积则是将$y=Cx$中的输入输出互换：
$$\begin{gathered} y=Cx \\ x=C^{T}y \end{gathered}$$
其中，$C^T$为矩阵$C$的转置，大小为$9\times 4$。

$4\times 1$的输入$y$经过$C^T$后，得到输出大小为$9\times 1$的列向量$x$，此时的$x,y$数值上已经和原来不同，只是在形状上一致。

stride的影响

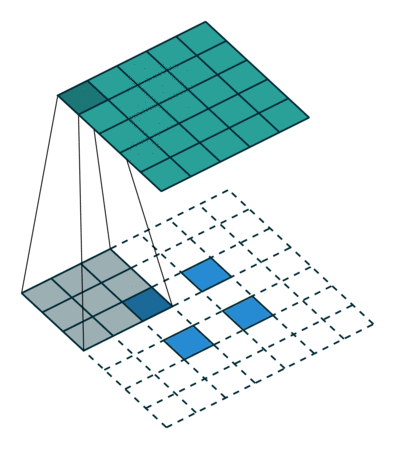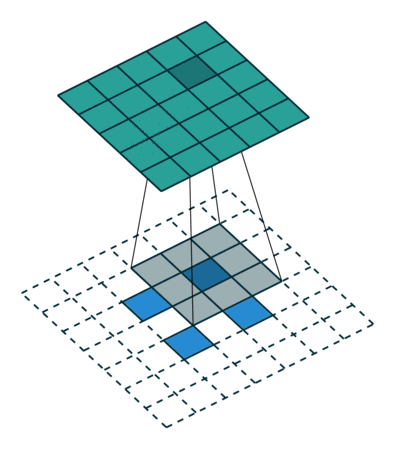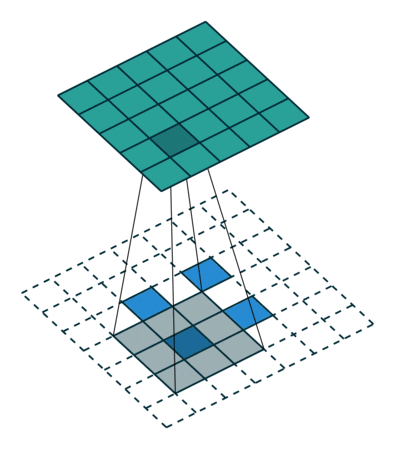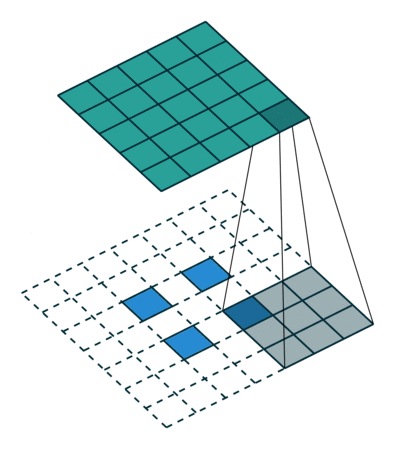
在实际中，我们大多数时候会使用 stride>1 的转置卷积，从而获得较大的上采样倍率。当$stride=2,|padding=0$，时，对于$5\times 5$的输入使用$3\times 3$的卷积核得到尺寸为$2\times 2$的输出矩阵，经过类似上述的推导后可知，这样的操作等同于添加了空洞和填充。对该输出使用转置后的标准卷积核进行计算，过程如图所示。

更一般地，对于卷积核尺寸 $kerne{l}_{size}=k$，步长 $stride=s>1$，填充 $padding=p=0$ 的转置卷积，其 等价的标准卷积 在原尺寸为 $i^{\prime }$ 的输入矩阵上进行运算，输出特征图的尺寸 $o^{\prime }$ 为：
$$o^{\prime }=s(i^{\prime }-1)+k$$
同时，等价的标准卷积的输入矩阵 input 在卷积运算前，需先进行 $paddin{g}^{\prime }=k-1$的填充，然后相邻元素的空洞数为$s-1$，共有$i^{\prime }-1$组空洞需要插入；从而，实际尺寸为$i^{\prime \prime }=i^{\prime }+2(k-1)+(i^{\prime }-1)\times (s-1)=s\times (i^{\prime }-1)+2k-1$。

因此，实际上原计算公式为（等价的标准卷积的步长$s^{\prime }=1$）：
$$o^{\prime }=\frac{i^{\prime \prime }-k+2p}{s^{\prime }}+1=s(i^{\prime }-1)+2k-1-k+1=s(i^{\prime }-1)+k$$
可见，通过控制步长 $stride=s$ 的大小可以控制上采样的倍率，而该参数类比于膨胀/空洞卷积的 膨胀率/空洞数。

$1\times 1$卷积

基础概念

1×1卷积最初提出的目的是用于增强模型对特定感受野下的局部区域的判定能力。 后续也被**GoogleNet[8]和ResNet[9]**进一步的应用。当卷积核尺寸为1x1时的卷积，也即卷积核变成只有一个数字。如下图：

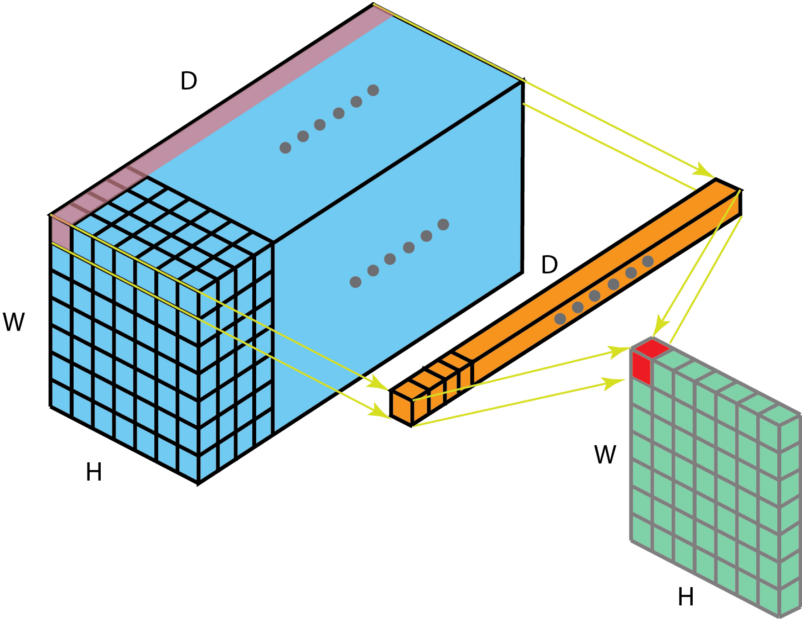
上图解释了$1\times 1$卷积如何适用于尺寸为$H\times W\times D$的输入层，滤波器大小为$1\times 1\times D$，输出通道的尺寸为$H\times W\times 1$。如果应用$n$个这样的滤波器，然后组合在一起，得到的输出层大小为$H\times W\times n$。

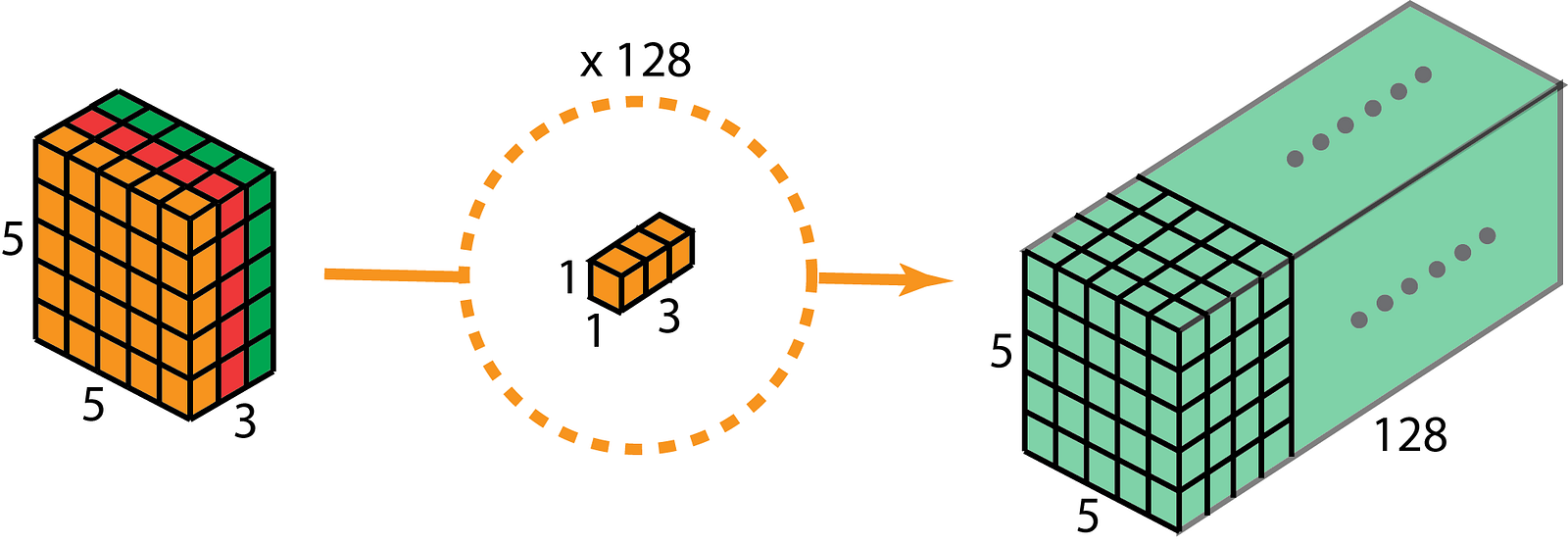
作用

1. 调节通道数

由于$1\times 1$卷积并不会改变 height 和 width，改变通道的第一个最直观的结果，就是可以将原本的数据量进行增加或者减少。这里看其他文章或者博客中都称之为升维、降维。但实际情况维度并没有改变，改变的只是通道数$C$这一个维度的大小而已。

2. 增加非线性

$1\times 1$卷积核，可以在保持特征图尺度不变的（即不改变）的前提下大幅增加非线性特性（利用后接的非线性激活函数如ReLU）。非线性允许网络学习更复杂的功能，并且使得整个网络能够进一步加深。

3. 跨通道信息

使用$1\times 1$卷积核，实现降维和升维的操作其实就是间通道信息的线性组合变化。例如：在卷积核大小为$3\times 3$，卷积核个数为64的滤波器与卷积核大小为$1\times 1$，卷积核个数为28的滤波器组合，其输出层大小等于通过卷积核大小为$3\times 3$，卷积核个数为28的滤波器所得到的输出层的大小，原来的64个通道就可以理解为跨通道线性组合变成了28通道，这就是通道间的信息交互。

4. 减少参数

前面所说的降维，其实也是减少了参数，因为特征图少了，参数也自然跟着就减少，相当于在特征图的通道数上进行卷积，压缩特征图，二次提取特征，使得新特征图的特征表达更佳。

空洞卷积

基础概念

为扩大感受野，在卷积核里面的元素之间插入空格来“膨胀”内核，形成“空洞卷积”（或称膨胀卷积），并用膨胀率参数L表示要扩大内核的范围，即在内核元素之间插入L-1个空格。当L=1时，则内核元素之间没有插入空格，变为标准卷积。
如下图为膨胀率L=2的空洞卷积：

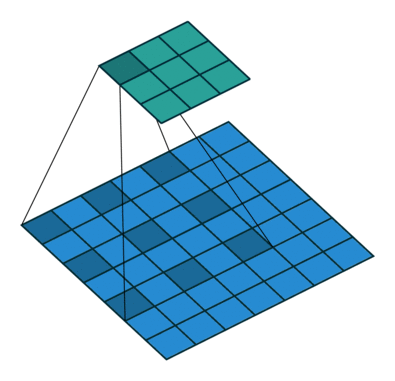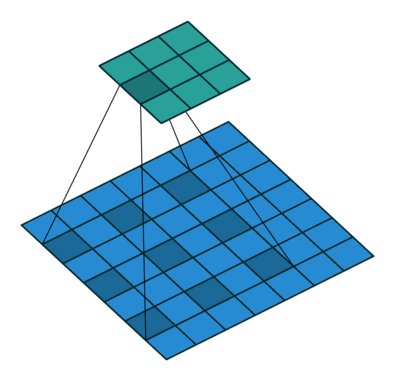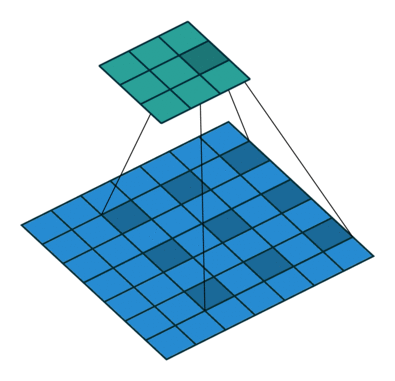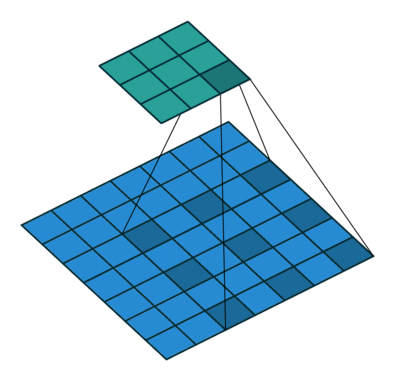
作用

• 扩大感受野：在deep net中为了增加感受野且降低计算量，总要进行降采样(pooling或s2/conv)，这样虽然可以增加感受野，但空间分辨率降低了。为了能不丢失分辨率，且仍然扩大感受野，可以使用空洞卷积。这在检测，分割任务中十分有用。一方面感受野大了可以检测分割大目标，另一方面分辨率高了可以精确定位目标。
• **捕获多尺度上下文信息：**空洞卷积有一个参数可以设置dilation rate，具体含义就是在卷积核中填充dilation rate-1个0，因此，当设置不同dilation rate时，感受野就会不一样，也即获取了多尺度信息。

空洞卷积可以任意扩大感受野，且不需要引入额外参数，但如果把分辨率增加了，算法整体计算量肯定会增加。空洞卷积虽然有诸多优点，但在实际中不好优化，速度会大大折扣。

相关计算

• 输出特征图大小

​ 设输入大小为$(H,W)$,滤波器大小为$(f_H,f_W)$,输出大小为$(o_H,o_W)$，填充为$p$,步幅为$s$。此时，输出大小为：
$$\begin{gathered} o_H=\frac{H+2p-f_H}{s}+1 \\ {o}_H=\frac{W+2p-f_W}{s}+1 \end{gathered}$$

• 感受野计算

$$R{F}_{i+1}=R{F}_i+(k-1)\times S_i$$

其中$R{F}_{I+1}$表示当前层的感受野，$R{F}_i$表示上一层的感受野，$k$表示卷积核的大小，$S_i$表示之前所有曾的步长的乘积（不包含本层）

深度可分离卷积

基础概念

深度可分离卷积由两步组成：深度卷积和1x1卷积。
首先，在输入层上应用深度卷积。如下图，使用3个卷积核分别对输入层的3个通道作卷积计算，再堆叠在一起。

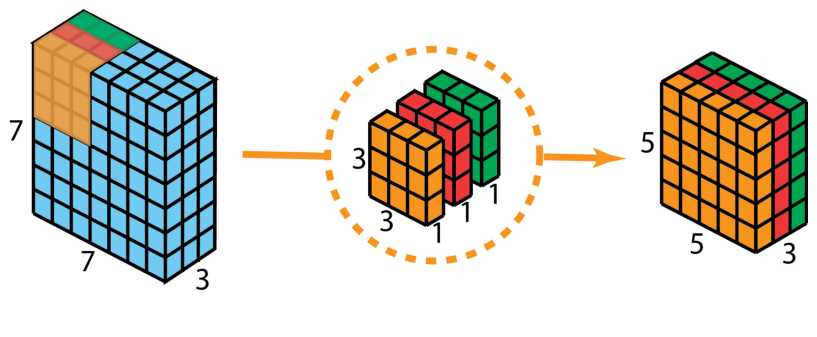
再使用1x1的卷积（3个通道）进行计算，得到只有1个通道的结果

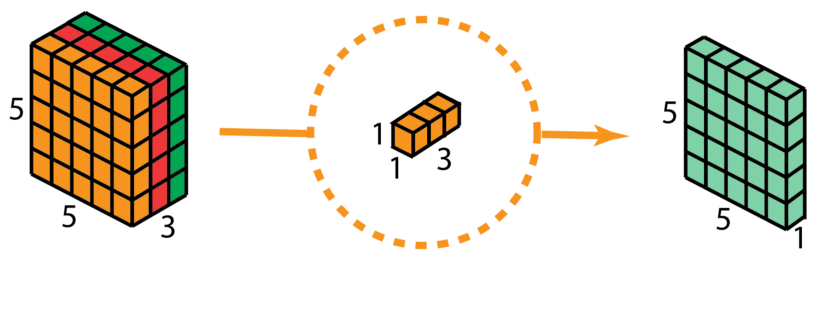
重复多次1x1的卷积操作（如下图为128次），则最后便会得到一个深度的卷积结果。

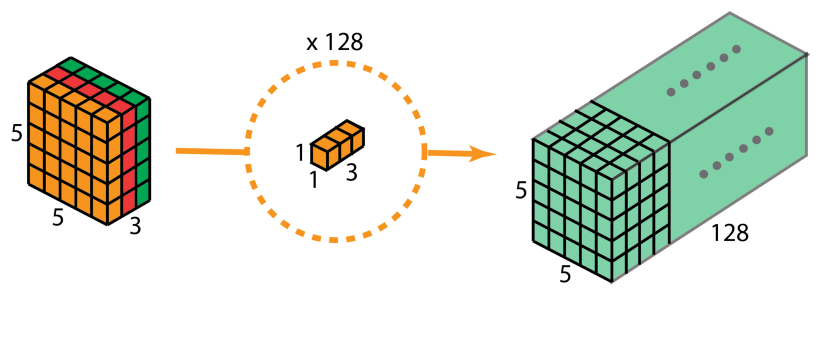
完整的过程如下：

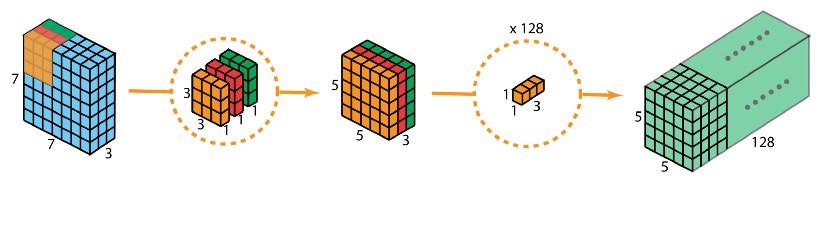
参数对比

假设输入特征图的尺寸为$D_k\times D_k\times M$，卷积核的尺寸为$D_F\times D_F\times M$，其数量为$N$。假设对应特征图空间位置中的每一个点都会进行一次卷及操作，那么可知单个卷积共需要进行$D_k\times D_k\times D_F\times D_F\times M$次计算。那么对$N$个卷积，其总计算量就为：$D_k\times D_k\times D_F\times D_F\times M\times N$。

对深度可分离卷积卷积进行分析可知：

逐通道卷积（Depthwise Convolution）计算总量为：
$$D_k\times D_k\times D_F\times D_F\times M$$
逐点卷积（Pointwise Convolution）的计算总量为：
$$M\times N\times D_k\times D_k$$
所以深度可分离卷积的计算总量为：
$$D_k\times D_k\times D_F\times D_F\times M+M\times N\times D_k\times D_k$$
那么相对于普通卷积，DSC的计算量与普通卷积的比值为：
$$\frac{1}{N}+\frac{1}{D_F^2}$$
简单总结一下，DSC作为普通卷积的一种替代品，它的最大优点是计算效率非常高。因此使用DSC构建轻量级模型是当下非常常见的做法。不过DSC的这种高效性是以低精度作为代价的。目前看来，设计高效率、高精度的DSC变体模块仍然是非常热点的研究方向之一。

可变形卷积（Deformable convolution）

出自论文Deformable Convolutional Networks

可变形卷积是指卷积核在每一个元素上额外增加了一个参数方向参数，这样卷积核就能在训练过程中扩展到很大的范围。

卷积核的目的是为了提取输入物的特征。我们传统的卷积核通常是固定尺寸、固定大小的（例如3x3，5x5，7x7.）。这种卷积核存在的最大问题就是，对于未知的变化适应性差，泛化能力不强。

卷积单元对输入的特征图在固定的位置进行采样；池化层不断减小着特征图的尺寸；RoI池化层产生空间位置受限的RoI。网络内部缺乏能够解决这个问题的模块，这会产生显著的问题，例如，同一CNN层的激活单元的感受野尺寸都相同，这对于编码位置信息的浅层神经网络并不可取，因为不同的位置可能对应有不同尺度或者不同形变的物体，这些层需要能够自动调整尺度或者感受野的方法。再比如，目标检测虽然效果很好但是都依赖于基于特征提取的边界框，这并不是最优的方法，尤其是对于非网格状的物体而言。解决上述问题最直观的想法就是，我们的卷积核可以根据实际情况调整本身的形状，更好的提取输入的特征。

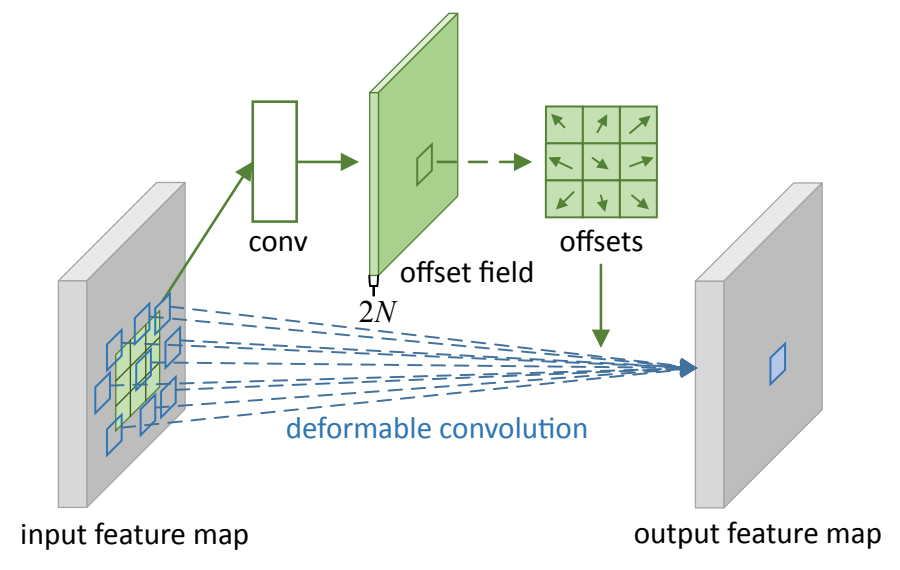
上图是可变形卷积的学习过程，首先偏差是通过一个卷积层获得，该卷积层的卷积核与普通卷积核一样。输出的偏差尺寸和输入的特征图尺寸一致。生成通道维度是2N，分别对应原始输出特征和偏移特征。这两个卷积核通过双线性插值后向传播算法同时学习。事实上，可变形卷积单元中增加的偏移量是网络结构的一部分，通过另外一个平行的标准卷积单元计算得到，进而也可以通过梯度反向传播进行端到端的学习。加上该偏移量的学习之后，可变形卷积核的大小和位置可以根据当前需要识别的图像内容进行动态调整，其直观效果就是不同位置的卷积核采样点位置会根据图像内容发生自适应的变化，从而适应不同物体的形状、大小等几何形变。然而，这样的操作引入了一个问题，即需要对不连续的位置变量求导。作者在这里借鉴了之前Spatial Transformer Network和若干Optical Flow中warp操作的想法，使用了bilinear插值将任何一个位置的输出，转换成对于feature map的插值操作。同理，类似的想法可以直接用于 (ROI) Pooling中改进。

空间可分离卷积(Spatially Separable Convolution)

空间可分离卷积是将卷积核分解为两项独立的核分别进行操作。一个3x3的卷积核分解如下图：

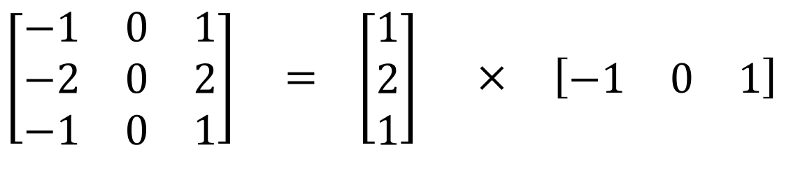
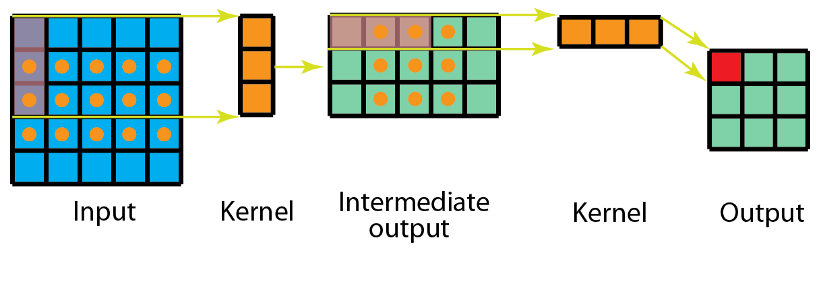
分解后的卷积计算过程如下图，先用3x1的卷积核作横向扫描计算，再用1x3的卷积核作纵向扫描计算，最后得到结果。采用可分离卷积的计算量比标准卷积要少。两次卷积，每次3次乘法（总共6次），乘法较少，计算复杂性下降，网络运行速度更快。

幻影卷积（Ghost Convolution）

众所周知，通过堆叠卷积层可以捕获丰富的特征信息，其中也包含了冗余信息，这有利于网络对数据有更全面的理解。因此，可以通过常规卷积操作提取丰富的特征信息，对于冗余的特征信息，则利用更价廉的线性变换操作来生成，这样不仅能够有效地降低模型所需计算资源，同时设计简单、易于实现，可以即插即用。

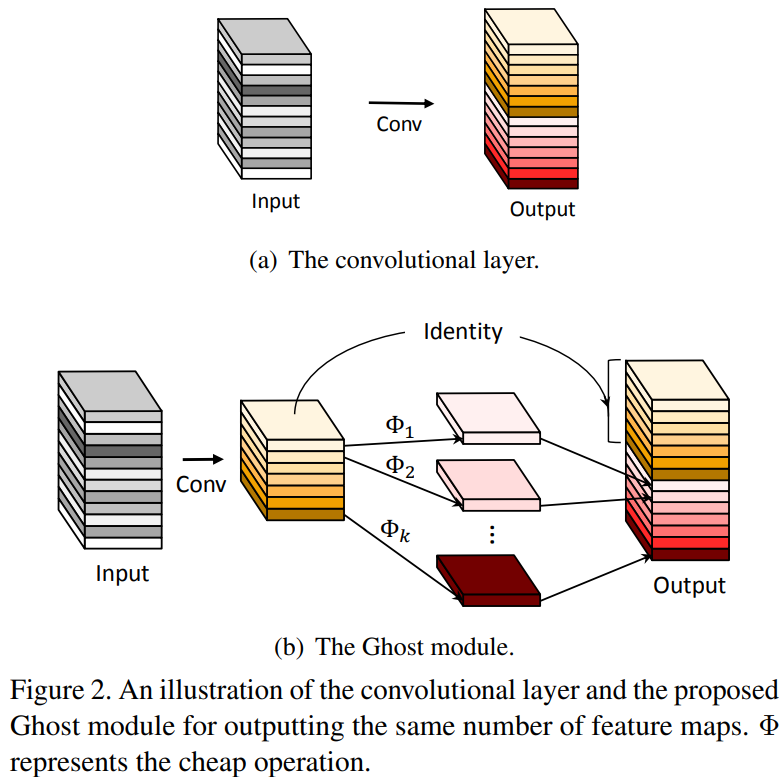
如上图所示，GhostNet模型首先利用少量的卷积核对输入特征图进行特征提取，然后进一步地对这部分特征图进行更价廉的线性变化运算，最后通过Concatenation（拼接操作）生成最终的特征图。具体来讲，使用较少的卷积核（可以是$1\times 1$， $3\times 3$等等）得到一定通道数的特征图，然后对得到的每个通道特征图使用一些线性变换运算（原文中使用的仍然是卷积操作）进行特征的提取，为了减少计算量，采用了深度可分离卷积，得到的结果可以看作是经过前一层的一系列线性变换得到的；最后将两次卷积的输出特征图在通道维度上堆叠即可。

这个方法减少了非关键特征的学习成本：即通过组合少量卷积核与更廉价的线性变化操作代替常规卷积方式，从而有效降低对计算资源需求的同时，并不影响模型的性能。

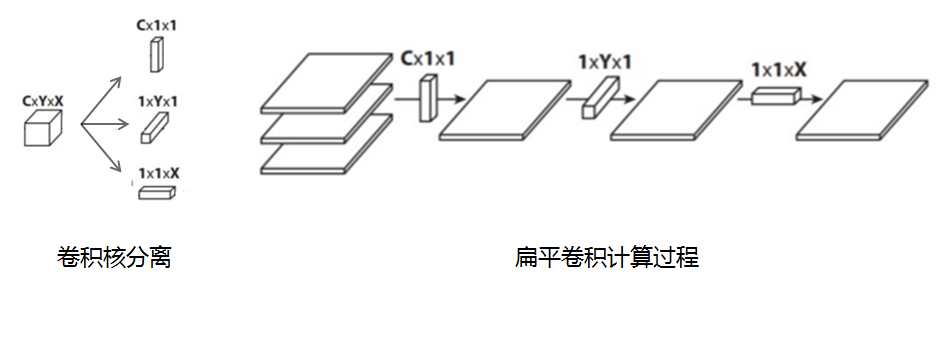
扁平卷积

扁平卷积是将标准卷积核拆分为3个1x1的卷积核，然后再分别对输入层进行卷积计算。这种方式，跟前面的“空间可分离卷积”类似，如下图：

总结与展望

本文介绍了卷积的一些常见变种，旨在进一步理解卷积的作用、经典思考等，为更加有效地搭建神经网络提供基础材料。对于相关模块的pytorch实现将在从零开始的深度学习实战篇（一）中介绍。

参考文献

[1] https://blog.csdn.net/qq_39478403/article/details/121181904

[2] https://zhuanlan.zhihu.com/p/115070523

[3] https://zhuanlan.zhihu.com/p/381839221

[4] https://zhuanlan.zhihu.com/p/166736637

[5] 【图解AI：动图】各种类型的卷积，你认全了吗？

[6] 可变形卷积从概念到实现过程

[7] https://arxiv.org/pdf/1911.11907.pdf

[8] https://zhuanlan.zhihu.com/p/50369448