扩散模型初探之DDPM

深度生成模型

深度生成模型已经打开了另一个人类创造力的深奥领域。通过捕捉和概括数据中的模式，我们进入了全方位人工智能创造力（AIGC）的时代。值得注意的是，扩散模型作为最重要的生成模型之一，将人类构思转化为可在多个领域实现的具体实例，包括图像、文本、语音、生物学和医疗保健等。

如何让机器拥有类似人类的想象力？深度生成模型，包括变分自动编码器（VAE）、能量基模型（EBM）、生成对抗网络（GAN）、归一化流（NF） 和扩散模型，展示了在生成逼真样本方面的显著潜力。扩散模型代表了这一领域的先进水平。这些模型有效地克服了诸如VAE中后验分布对齐的障碍、缓解GAN中固有的对抗目标的不稳定性、解决在EBM训练过程中与马尔可夫链蒙特卡洛（MCMC）方法相关的计算负担，以及施加类似NF的网络约束。因此，扩散模型在计算机视觉、自然语言处理、时间序列、音频处理、图生成 和生物信息学 等各个领域引起了极大关注。

扩散模型包括两个相互关联的过程：一个预先定义的正向过程，将数据分布映射到一个更简单的先验分布，通常是高斯分布；以及一个对应的逆过程，利用训练有素的神经网络逐渐逆转正向过程的效应，通过模拟常微分方程或随机微分方程（ODE/SDE）。正向过程类似于一个具有时间变化系数的简单布朗运动。神经网络经过训练，利用去噪得分匹配目标来估计得分函数。因此，与GAN中采用的对抗目标相比，扩散模型提供了更稳定的训练目标，并且在生成质量方面优于VAE、EBM和NF。然而，需要强调的是，与GAN和VAE相比，扩散模型本质上需要更耗时的采样过程。这是由于通过使用常微分方程/随机微分方程（ODE/SDE）或马尔可夫过程将先验分布迭代转化为复杂的数据分布，需要在逆过程中进行大量的函数评估。此外，其他挑战包括逆过程的不稳定性，与在高维欧几里得空间中训练相关的计算要求和约束，以及涉及可能性优化的复杂性。为了应对这些挑战，研究人员提出了各种解决方案。例如，提出了先进的ODE/SDE求解器来加速采样过程，同时采用了模型蒸馏策略 来实现相同的目标。此外，还引入了新颖的正向过程，以增强采样稳定性或促进降维。此外，最近的一系列研究尝试利用扩散模型有效地桥接任意分布。为了提供系统性的概览，我们将这些进展划分为四个主要领域：采样加速、扩散过程设计、可能性优化和桥接分布。

扩散模型初探

说到扩散模型，一般的文章都会提到能量模型（Energy-based Models）、得分匹配（Score Matching）、朗之万方程（Langevin Equation）等等，简单来说，是通过得分匹配等技术来训练能量模型，然后通过郎之万方程来执行从能量模型的采样。

从理论上来讲，这是一套很成熟的方案，原则上可以实现任何连续型对象（语音、图像等）的生成和采样。但从实践角度来看，能量函数的训练是一件很艰难的事情，尤其是数据维度比较大（比如高分辨率图像）时，很难训练出完备能量函数来；另一方面，通过朗之万方程从能量模型的采样也有很大的不确定性，得到的往往是带有噪声的采样结果。所以很长时间以来，这种传统路径的扩散模型只是在比较低分辨率的图像上做实验。

如今生成扩散模型的大火，则是始于2020年所提出的DDPM（Denoising Diffusion Probabilistic Model），虽然也用了“扩散模型”这个名字，但事实上除了采样过程的形式有一定的相似之外，DDPM与传统基于朗之万方程采样的扩散模型可以说完全不一样，这完全是一个新的起点、新的篇章。

准确来说，DDPM叫“渐变模型”更为准确一些，扩散模型这一名字反而容易造成理解上的误解，传统扩散模型的能量模型、得分匹配、朗之万方程等概念，其实跟DDPM及其后续变体都没什么关系。有意思的是，DDPM的数学框架其实在ICML2015的论文《Deep Unsupervised Learning using Nonequilibrium Thermodynamics》就已经完成了，但DDPM是首次将它在高分辨率图像生成上调试出来了，从而引导出了后面的火热。由此可见，一个模型的诞生和流行，往往还需要时间和机遇，

DDPM模型概述

DDPM包括两个过程：前向过程（forward process）和反向过程（reverse process），其中前向过程又称为扩散过程（diffusion process），如下图所示。无论是前向过程还是反向过程都是一个参数化的马尔可夫链（Markov chain），其中反向过程可以用来生成数据。

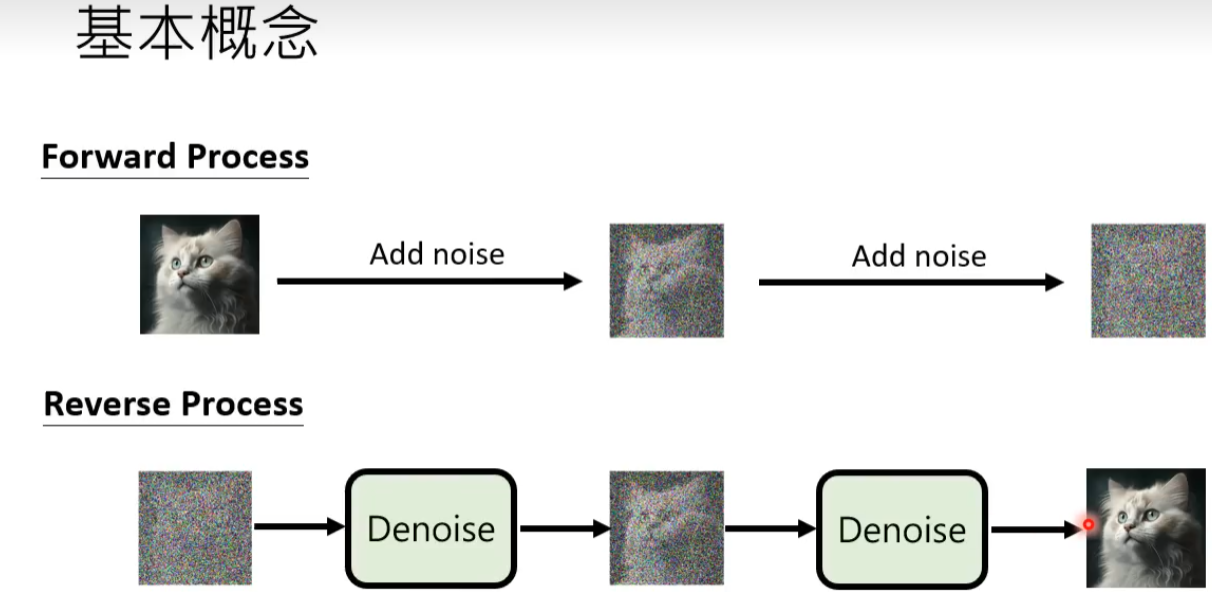
前向过程（Diffusion Process）

前向过程是指对数据逐渐增加高斯噪音直至数据变成随机噪音的过程。对于原始数据$x_0\sim q(x_0)$，总共包含$T$步的扩散过程的每一步都是对上一步得到的数据$x_{t-1}$按如下方式增加高斯噪音
$$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},\sqrt{{\beta }_t}I)\text{\hspace{1em}(1a)}$$
该式同样可写为：
$$x_t=\sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{\epsilon }_t,{\epsilon }_t\sim \mathcal{N}(0,I)\text{\hspace{1em}(1b)}$$
其中 { β t } t = 1 T \{\beta_t\}^T_{t=1} {βt​}t=1T​为每一步所采用的方差，介于0到1之间。对于扩散模型，我们往往称不同step的方差设定为variance schedule或者noise schedule，通常情况下，越后面的step会采用更大的方差，即满足${\beta }_1<{\beta }_2<\cdots <{\beta }_T$。在一个设计好的variance schedule下，如果step数$T$足够大，那么最终得到的$x_t$就完全丢失了原始数据而变成了一个随机噪音。扩散过程的每一步都生成一个带噪音的数据$x_t$，整个扩散过程也就是一个马尔科夫链：
$$q(x_{1:T}|x_0)=\prod _{t=1}^{T}q(x_t|x_{t-1})\text{\hspace{1em}(2)}$$
实际上，任意时刻的$q(x_t)$推导也可以完全基于$x_0$和${\beta }_t$来计算，无需迭代：
$$\begin{array}{rl}{x}_t=& \sqrt{1-{\beta }_t}{x}_{t-1}+\sqrt{{\beta }_t}{\epsilon }_t\\ =& \sqrt{1-{\beta }_t}(\sqrt{1-{\beta }_{t-1}}{x}_{t-1}+\sqrt{{\beta }_{t-1}}{\epsilon }_{t-1})+\sqrt{{\beta }_t}{\epsilon }_t\\ =& \sqrt{1-{\beta }_t}\sqrt{1-{\beta }_{t-1}}{x}_{t-1}+\sqrt{1-{\beta }_t}\sqrt{{\beta }_{t-1}}{\epsilon }_{t-1}+\sqrt{{\beta }_t}{\epsilon }_t\\ =& \sqrt{1-{\beta }_t}\sqrt{1-{\beta }_{t-1}}{x}_{t-1}+\sqrt{{\beta }_t(1-{\beta }_{t-1})+{\beta }_{t-1}}\overline{{\epsilon }_t}\\ =& \sqrt{1-{\beta }_t}\sqrt{1-{\beta }_{t-1}}{x}_{t-1}+\sqrt{1-(1-{\beta }_t)(1-{\beta }_{t-1})}\overline{{\epsilon }_t}\\ =& \cdots \\ =& \sqrt{1-{\bar{\beta }}_t}{x}_0+\sqrt{{\bar{\beta }}_t}\epsilon \end{array}$$

其中，${\bar{\epsilon }}_t$是通过高斯分布混合得到的。对$\mathcal{N}(0,{\sigma }_1^{2}I)$和$\mathcal{N}(0,{\sigma }_2^{2}I)$两个高斯分布进行混合，得到新的分布：$\mathcal{N}(0,({\sigma }_1^2+{\sigma }_2^2)I)$，其中对应的标准差为：$\sqrt{{\beta }_t(1-{\beta }_{t-1})+{\beta }_{t-1}}=\sqrt{{\beta }_t(1-{\beta }_{t-1})-(1-{\beta }_{t-1})+1}=\sqrt{1-(1-{\beta }_t)(1-{\beta }_{t-1})}$

即$q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\bar{\beta }}_t}{x}_0,(1-{\bar{\alpha }}_t)I)$，其中${\bar{\beta }}_t={\beta }_1{\beta }_2\cdots {\beta }_t$

逆向过程（Reverse Process）

逆向过程是从高斯噪声中回复原始数据，我们可以假设它也是一个高斯分布，但是无法逐步地去拟合分布，所以需要构建一个参数分布来做估计。即根据上述信息中求出逆向过程所需要的$p(x_{t-1}|x_t)$，从而实现从任意一个$x_T=z$出发，逐步采样出$x_{T-1},x_{T-2},\cdots ,x_1$，最后得到随机生成的样本数据$x_0=x$。逆扩散过程仍然是一个马尔科夫链过程。
$$p_{\theta }(x_{0:T})=p(x_T)\prod _{t=1}^T{p}_{\theta }(x_{t-1}|x_t),p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\sum }_{\theta }(x_t,t))$$
根据贝叶斯定理有：
$$p(x_{t-1}|x_t)=\frac{p(x_t|x_{t-1})p(x_{t-1})}{p(x_t)}$$
由于$q(x_{t-1}),q(x_t)$是未知的，因此可以在给定的$x_0$的条件下使用贝叶斯定理：
$$p(x_{t-1}|x_t,x_0)=\frac{p(x_t|x_{t-1},x_0)p(x_{t-1}|x_0)}{p(x_t|x_0)}\text{\hspace{1em}(3)}$$
其中$p(x_t|x_{t-1},x_0),p(x_{t-1}|x_0),p(x_t|x_0)$均是已知的，代入各自的表达式得到：
$$\begin{array}{rl}p(x_{t-1}|x_t,x_0)& \propto exp(-\frac{1}{2}(\frac{(x_t-\sqrt{{\alpha }_t}{x}_{t-1}{)}^2}{{\beta }_t}+\frac{(x_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{x}_0{)}^2}{{\bar{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\bar{\alpha }}_t}{x}_0{)}^2}{1-{\bar{\alpha }}_t}))\\ & =exp(-\frac{1}{2}((\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})x_{t-1}^2-(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0)x_{t-1}+C(x_t,x_0)))\end{array}\text{\hspace{1em}(4)}$$
其中，$C(x_t,x_0)$是与$x_{t-1}$无关的项。

由高斯分布的概率密度函数以及平方和公式
$$\begin{array}{rl}& f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\\ & a{x}^2+bx=a(x+\frac{b}{2a}{)}^2+C\end{array}$$
可得，式(4)中$p(x_{t-1}|x_t,x_0)$的均值和方差为：
$$\begin{array}{rl}\bar{\mu }(x_t,x_0)=\mu =-\frac{b}{2a}& =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}+\frac{\sqrt{{\bar{\alpha }}_t}}{1-{\bar{\alpha }}_t}{x}_0)/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{x}_0\\ {\bar{\beta }}_t={\sigma }^2=\frac{1}{a}& =1/(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\end{array}\text{\hspace{1em}(5)}$$
至此，我们得到了完整的$p(x_{t-1}|x_t,x_0)$表达式，即
$$p(x_{t-1}|x_t,x_0)=\mathcal{N}(x_{t-1};\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{{\bar{\alpha }}_{t-1}{\beta }_t^2}{{\bar{\beta }}_t^2}{x}_0,\frac{{\bar{\beta }}_{t-1}{\beta }_t^2}{{\bar{\beta }}_t^2}I)\text{\hspace{1em}(6)}$$
此时，我们得到了$p(x_{t-1}|x_t,x_0)$，但这并非我们期望的最终答案，我们的目的是通过$x_t$来预测$x_{t-1}$，而不能依赖$x_0$，$x_0$是我们最终想要生成的结果。

如果我们能够通过$x_t$来预测$x_0$，那么就可以使得$p(x_{t-1}|x_t,x_0)$仅依赖于$x_t$。

为了实现这个目的，我们通过$\bar{\mu }(x_t)$来预估$x_0$，损失函数为$||x_0-\bar{\mu }(x_t)|{|}^2$。训练完成后，我们认为：
$$p(x_{t-1}|x_t)\approx p(x_{t-1}|x_t,x_0=\bar{\mu }(x_t))=\mathcal{N}(x_{t-1};\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{{\bar{\alpha }}_{t-1}{\beta }_t^2}{{\bar{\beta }}_t^2}\bar{\mu }(x_t),\frac{{\bar{\beta }}_{t-1}{\beta }_t^2}{{\bar{\beta }}_t^2}I)$$
由前向过程推导可知$x_0$与$x_t$的关系：
$$x_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}\epsilon )$$
代入式（5）可得：
$$\begin{array}{rl}\bar{\mu }(x_t)& =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{x}_0\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{x}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\cdot \frac{1}{\sqrt{{\bar{\alpha }}_t}}(x_t-\sqrt{1-{\bar{\alpha }}_t}\epsilon )\\ & =[\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t/\sqrt{{\bar{\alpha }}_t}}{1-{\bar{\alpha }}_t}]x_t-\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t\sqrt{1-{\bar{\alpha }}_t}}{\sqrt{{\bar{\alpha }}_t}1-{\bar{\alpha }}_t}\epsilon \\ & =[\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}+\frac{{\beta }_t/\sqrt{{\alpha }_t}}{1-{\bar{\alpha }}_t}]x_t-\frac{{\beta }_t}{\sqrt{{\alpha }_t}\sqrt{1-{\bar{\alpha }}_t}}\epsilon \\ & =\frac{{\alpha }_t(1-{\bar{\alpha }}_{t-1})+{\beta }_t}{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_t)}{x}_t-\frac{{\beta }_t}{\sqrt{{\alpha }_t}\sqrt{1-{\bar{\alpha }}_t}}\epsilon \\ & =\frac{{\alpha }_t-{\bar{\alpha }}_t+{\beta }_t}{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_t)}{x}_t-\frac{{\beta }_t}{\sqrt{{\alpha }_t}\sqrt{1-{\bar{\alpha }}_t}}\epsilon \\ & =\frac{1-{\bar{\alpha }}_t}{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_t)}{x}_t-\frac{{\beta }_t}{\sqrt{{\alpha }_t}\sqrt{1-{\bar{\alpha }}_t}}\epsilon \\ & =\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}\epsilon )\end{array}\text{\hspace{1em}(7)}$$
则损失函数变为：
$$||x_0-\bar{\mu }(x_t)|{|}^2=\frac{{\bar{\beta }}_t}{{\bar{\alpha }}_t}||\epsilon -{ϵ}_{\theta }(\sqrt{{\bar{\alpha }}_t}{x}_0+\sqrt{{\bar{\beta }}_t}\epsilon ,t)|{|}^2$$

文生图应用初窥

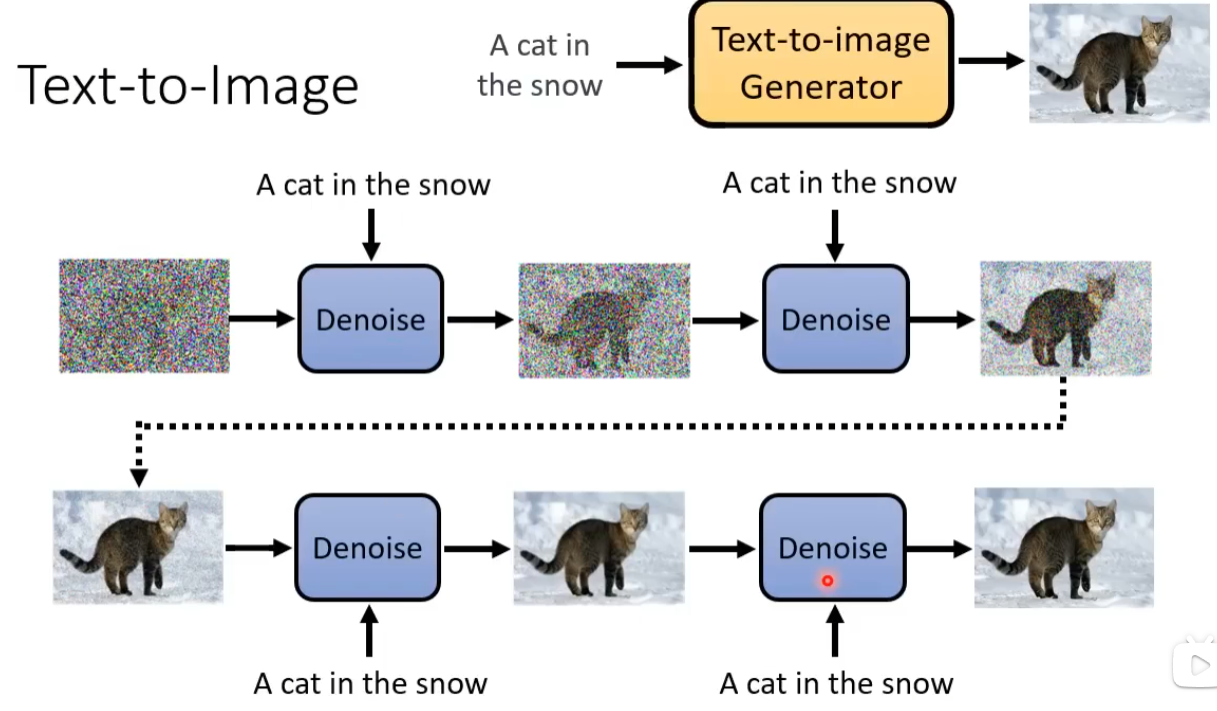
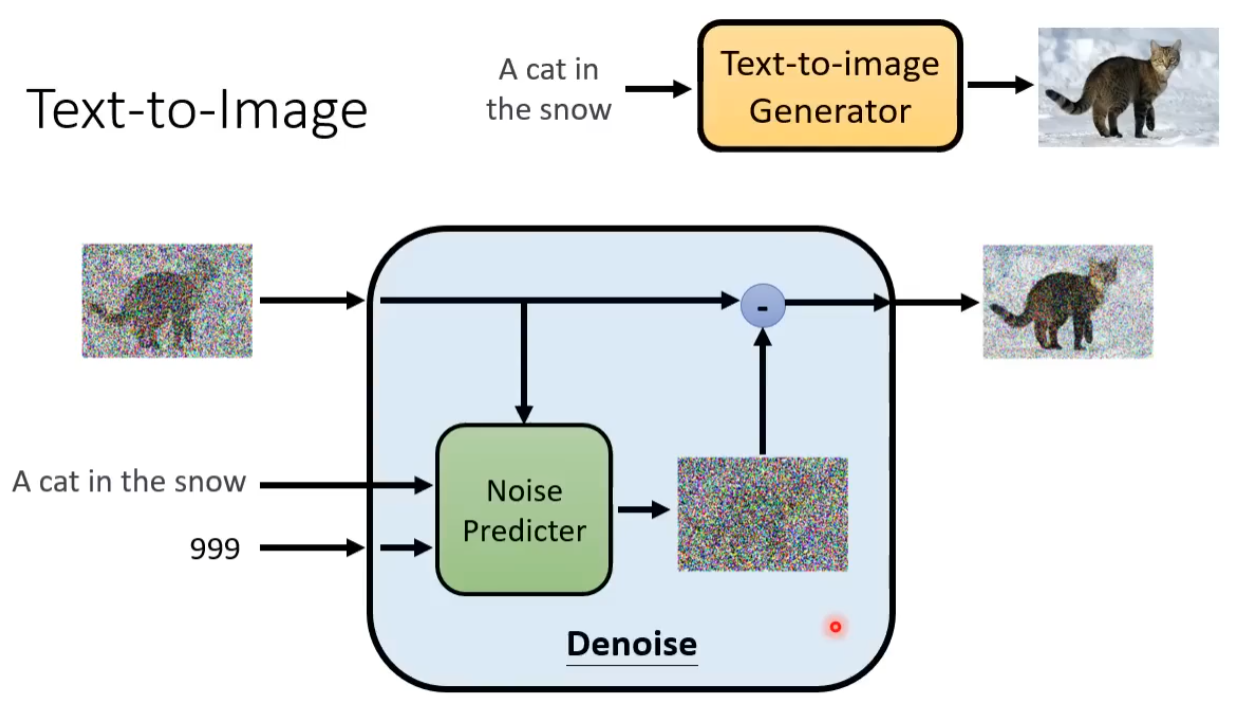
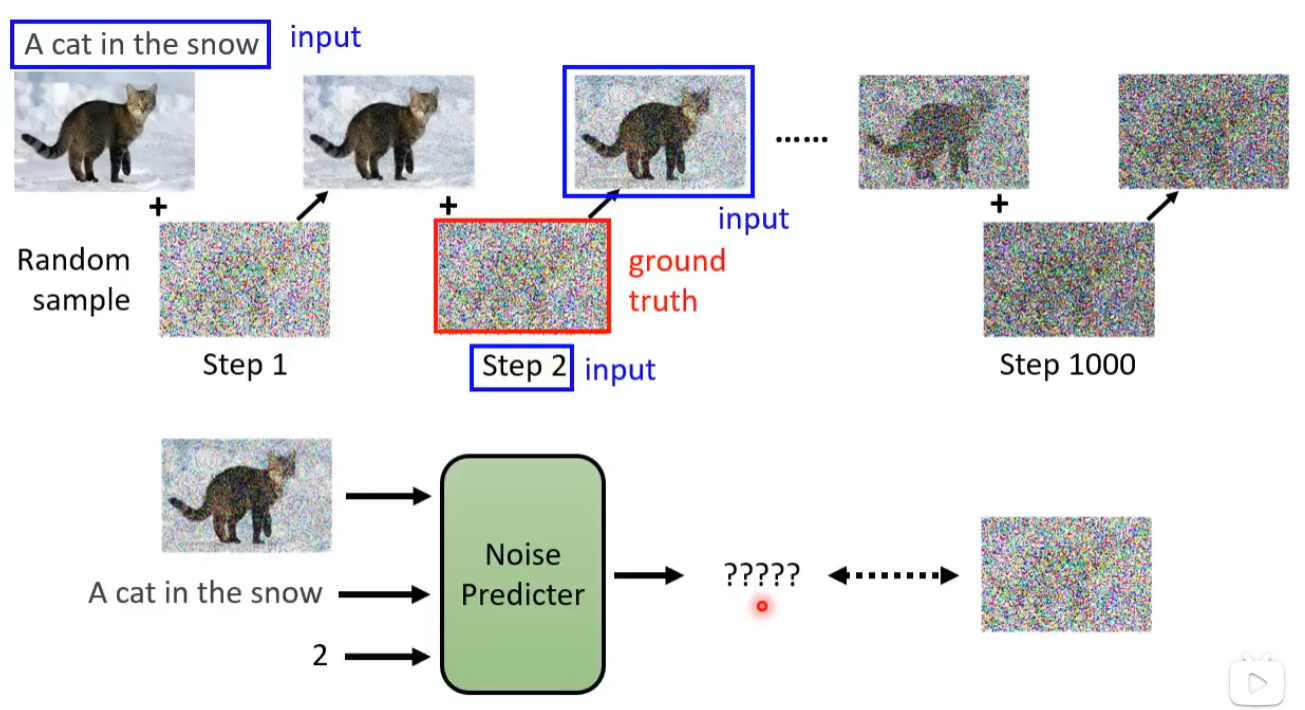
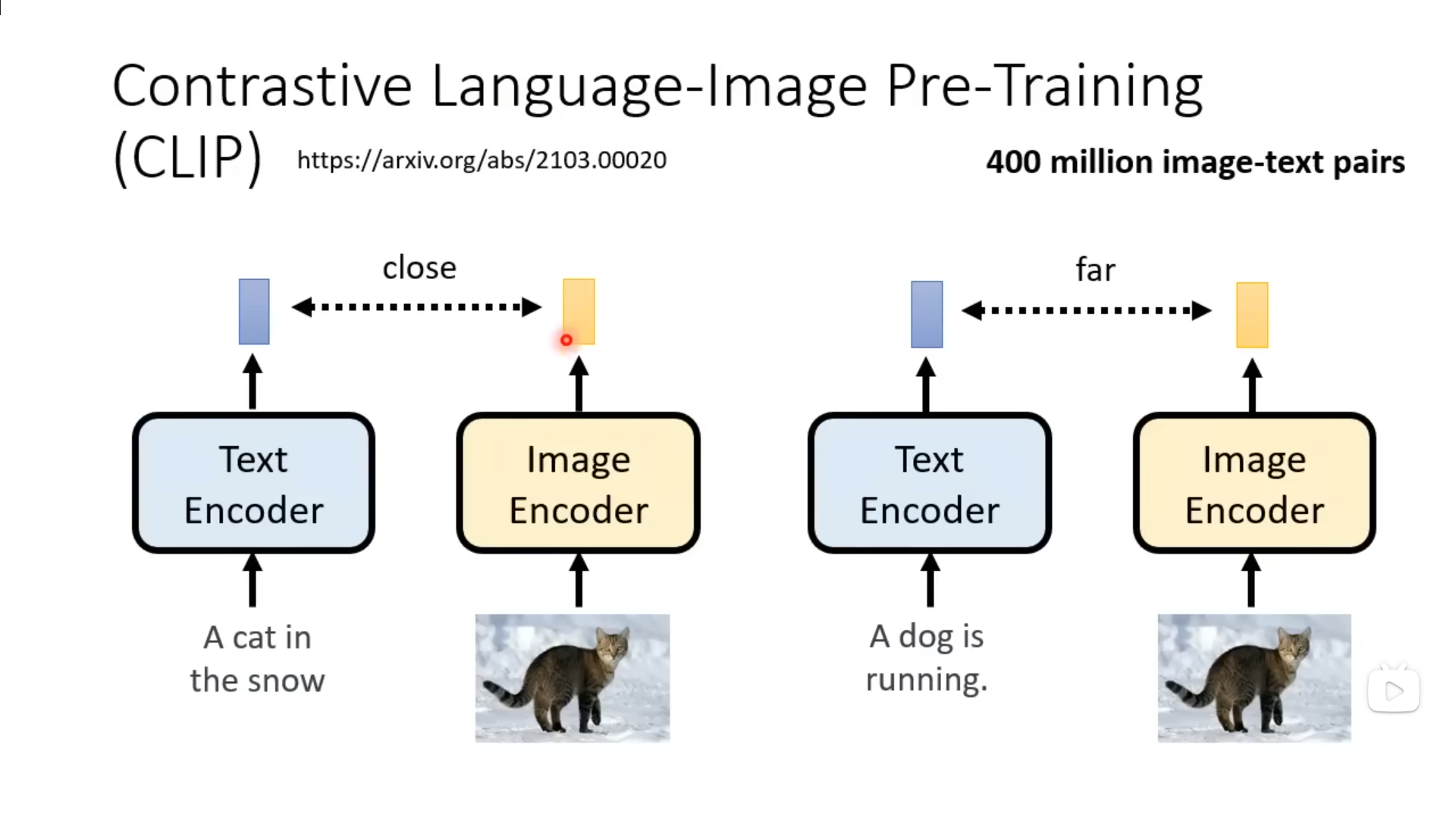
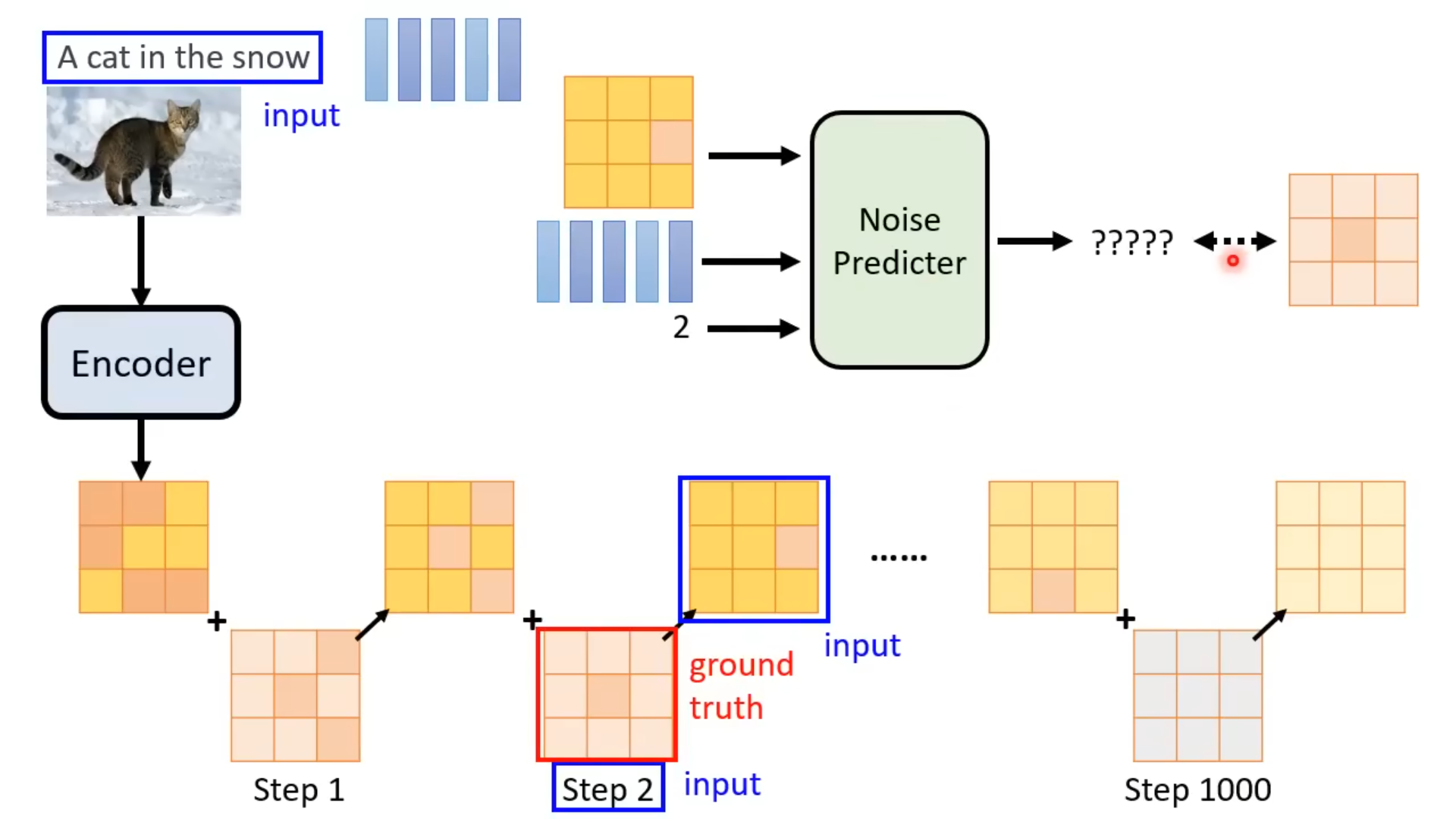
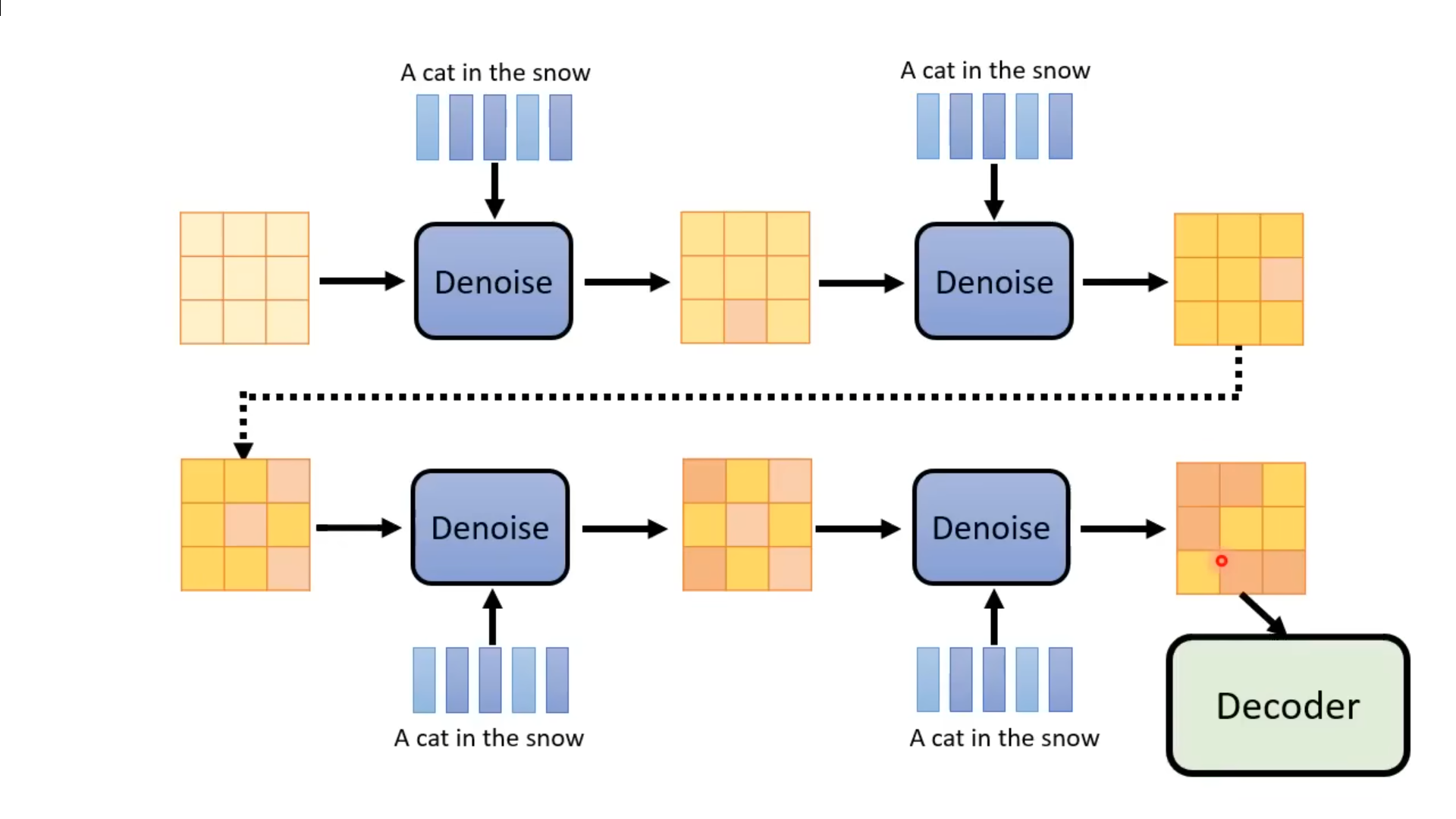
基于原始的扩散模型，利用文本图像对进行文生图训练。在使用Noise Predicter进行Denoise时，将文本输入到Noise Predicter模块进行约束。为了将文本输入到模型中，并让模型效率更高，基于LLM进行自然语言文本的编码，经过Text Encoder后得到向量化的文本，基于扩散模型得到结果后，使用Decoder得到最终的图像。其中，Decoder一般是一个将图像放大的模块，从而实现在生成模型中使用较小特征图进行推理，将推理结果使用decoder得到目标图片。

参考文献

https://t.bilibili.com/700526762586538024

https://kexue.fm/archives/9164

https://zhuanlan.zhihu.com/p/637815071

https://zhuanlan.zhihu.com/p/563661713

https://medium.com/@gitau_am/a-friendly-introduction-to-denoising-diffusion-probabilistic-models-cc76b8abef25

https://arxiv.org/abs/2209.02646