SLAM十四讲【三】李群与李代数

SLAM十四讲【三】李群与李代数

SLAM十四讲【一】基本概念
SLAM十四讲【二】三维空间刚体运动
SLAM十四讲【三】李群与李代数
SLAM十四讲【四】相机与图像
SLAM十四讲【五】线性优化
SLAM十四讲【六】视觉里程计
SLAM十四讲【七】回环检测
SLAM十四讲【八】建图

---

一、李群与李代数基础

1.1 群

  两个旋转矩阵或者变换相加就不是原来矩阵的类型了，但乘却是代表做了两次运算，还是原来的类型，对于这种只有一个运算的集合就称之为群。
  群(Group)是一种集合加上一种运算的代数结构。我们把集合记作A,运算记作·，那么群可以记作 G=(A,·)。 群要求这个运算满足以下几个条件：
  1.封闭性： 任意a1 , a2∈A , a1·a2∈A .
  2.结合律： 任意a1 ,a2, a3∈A , (a1·a2)·a3=a1·(a2·a3) .
  3.幺元： 任意a0∈A , s.t. 任意a∈A ,a0·a=a·a0=a .
  4.逆： 任意a∈A , 存在a^(-1)∈A , s.t. a·a^(-1)=a0 .
  矩阵中常见的群有：
  一般线性群GL(n)：指 n*n 的可逆矩阵，它们对矩阵乘法成群。
  特殊正交群SO(n)：也就是所谓的旋转矩阵群，其中SO(2)和SO(3)最为常见。
  特殊欧氏群SE(n)：也就是前面提到的n维欧氏变换，如SE(2)和SE(3)。
  挪威数学家Sophus Lie （索菲斯·李）提出了“李群”的核心理论。李群是指具有连续（光滑）性质的群。像整数群Z那样离散的群没有连续性质，所以不是李群。而SO(n)和SE(n)在实数空间上是连续的。我们能够直观地想象一个刚体能够连续地在空间中运动，所以它们都是李群。由于SO(3)和SE(3)对于相机姿态估计尤其重要，所以我们主要讨论这两个李群。

1.2 李代数的引出

  对于任意旋转矩阵R，满足

  这种旋转会随着时间连续的变化成为时间的函数，有

  求导得

  整理得

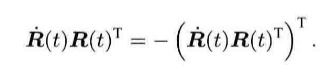
  这里的R(t)R(t)^T 是一个反对称矩阵，会有一个唯一向量对应

  三维向量 φ(t)∈R³ 与之对应

  带入同乘R(t)，有

  把R(t)在t=0附近进行一阶泰勒展开

  φ反映了R的导数性质，故称它在SO(3)原点附近的正切空间，设φ保持为常数 φ(t0)=φ0，有

  有初始值R(0)=I,解得

  这样，旋转矩阵可以由exp(φ0^t) 计算出来。

1.3 李代数的定义

  每个李群都有与之对应的李代数。李代数描述了李群的局部性质，准确地说，是单位元附近的正切空间。一般的李代数的定义如下：李代数由一个集合V、一个数域F和一个二元运算[，]组成。如果它们满足以下几条性质，则称(V,F,[,])为一个李代数，记作g。
  1.封闭性VX, Y∈V , [X,Y]∈V .
  2.双线性VX,Y Z∈V a, b∈F ,有[aX+bY,Z]=a[X,Z]+b[Y,Z] , [Z,aX+bY]=a[Z,X]+b[Z,Y] .
  3.自反性 X∈V , [X,X]=0 .
  4.雅可比等价VX,Y Z∈V [X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0.
  其中二元运算被称为李括号。

1.4 李代数SO(3)

  之前提到的，事实上是一种李代数。SO(3)对应的李代数是定义在R3上的向量，我们记作φ。根据前面的推导，每个φ都可以生成一个反对称矩阵：

  在此定义下，两个向量φ1,φ2的李括号为

  我们可以说so(3)的元素是三维向量或者三维反对称矩阵

1.5 李代数SE(3)

  对于SE(3),它也有对应的李代数se(3)。

  把每个se(3)元素记作，它是一个六维向量。前三维为平移（但含义与变换矩阵中的平移不同，分析见后)，记作p;后三维为旋转，记作，实质上是so(3)元素 。同时，我们拓展了 ^ 符号的含义。在se(3)中，同样使用^符号，将一个六维向量转换成四维矩阵，但这里不再表
示反对称：

二、指数与对数映射

2.1 SO(3)上的指数映射

  exp(φ^)显然它是一个矩阵的指数，在李群和李代数中，
称为指数映射(ExponentialMap)。任意矩阵的指数映射可以写成一个泰勒展开，但是只有在收敛的情况下才会有结果，其结果仍是一个矩阵：

  同样地，对so(3)中的任意元素，我们也可按此方式定义它的指数映射：

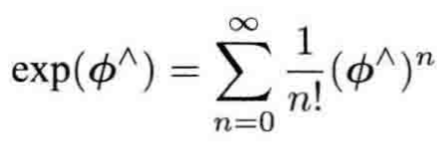
  由于是三维向量，我们可以定义它的模长和方向，分别记作θ和a，于是有φ=θa。 这里a是一个长度为1的方向向量，即||a||=1。首先，对于a^，有以下两条性质：


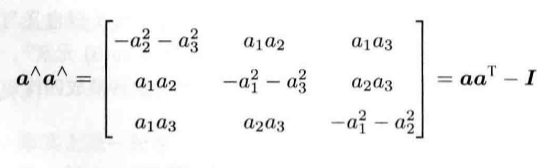
  那么就可以把指数映射写成

  最后得到

  我们把so(3)中任意一个向量对应到了一个位于SO(3)中的旋转矩阵。反之，如果定义对数映射，也能把SO(3)中的
元素对应到so(3)中：

  因为旋转360°和没有转是一样的，把旋转角度固定在±π之间，那么李群和李代数元素是一一对应的。

2.2 SE(3)上的指数映射

  se(3)上的指数映射形式如下：

  把exp进行泰勒展开推导此式。令 φ=θa ，其中a为单位向量，则


  右上角的t满足：

  李群和李代数总的对应关系如下：

三、李代数求导与扰动模型

3.1 BCH公式与近似形式

  两个李代数指数映射乘积的完整形式，由Baker-Campbell-
Hausdorff公式(BCH公式)给出。由于其完整形式较复杂，我们只给出其展开式的前几项：

  其中[]为李括号。BCH公式告诉我们，当处理两个矩阵指数之积时，它们会产生一些由李括号组成的余项。当φ为小量时，小量二次以上的项都可以被忽略。此时，BCH拥有线性近似表达：

  以第一个近似为例。该式告诉我们，当对一个旋转矩阵 R2 (李代数为转矩阵R1(李代数为φ1)时，可以近似地看作，在原有的李数左乘一个微小旋上加上了一项 Jl(φ2)^(-1)φ1。同理，第二个近似描述了右乘一个微小位移的情况。于是，李代数在BCH近似下，分成了左乘近似和右乘近似两种，在使用时我们须注意使用的是左乘模型还是右乘模型，以左乘为例。左乘BCH近似雅可比J：

  它的逆就是

  如果右乘雅可比只需要对自变量取负号即可：

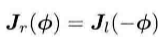
  李群乘法：假定对某个旋转R,对应的李代数为φ，我们给它左乘一个微小旋转，记作△R,对应的李代数为△φ。那么，在李群上，得到的结果就是△R·R，而在李代数上，根据BCH近似，为为Jl(φ)^(-1)△φ+φ。合并起来，可以简单地写成：

  李群加法：在李代数上进行加法，让一个φ加上△φ，那么可以近似为李群上带左右雅可比的乘法：

3.2 SO(3)上的李代数求导

  在SLAM中，我们要估计一个相机的位置和姿态，该位姿是由SO(3)上的旋转矩阵或SE(3)上的变换矩阵描述的。不妨设某个时刻小萝卜的位姿为T。它观察到了一个世界坐标位于p的点，产生了一个观测数据z。那么，由坐标变换关系知：

  其中w为随机噪声。由于它的存在，z往往不可能精确地满足z=Tp的关系。所以，我们通常会计算理想的观测与实际数据的误差：

  假设一共有N个这样的路标点和观测，于是就有N个上式。那么，对小萝卜进行位姿估计，相当于寻找一个最优的T,使得整体误差最小化：

  使用李代数解决求导问题的思路分为两种：
  1.用李代数表示姿态，然后根据李代数加法对李代数求导。
  2.对李群左乘或右乘微小扰动，然后对该扰动求导，称为左扰动和右扰动模型。
  第一种方式对应到李代数的求导模型，而第二种方式则对应到扰动模型。

3.2 李代数求导

  首先，考虑SO(3)上的情况。假设我们对一个空间点p进行了旋转，得到了Rp。现在，要计算旋转之后点的坐标相对于旋转的导数，我们非正式地记为

  由于SO(3)没有加法，所以该导数无法按照导数的定义进行计算。设R对应的李代数为φ，我们转而计算：

  按照导数的定义，有

  通过BCH线性近似、泰勒展开近似和反对称矩阵，可以推导出旋转后的点相对于李代数的导数：

  这里的雅可比还是有点复杂，扰动模型提供了更简单的导数计算方式。

3.3 扰动模型(左乘)

  另一种求导方式是对R进行一次扰动△R,看结果相对于扰动的变化率。这个扰动可以乘在左边也可以乘在右边，最后结果会有一点儿微小的差异，我们以左扰动为例。设左扰动△R对应的李代数为 φ。然后，对φ求导，即


  相比于李代数求导，这样就不用计算雅可比了。

3.4 E(3)上的李代数求导

  最后，给出SE(3)上的扰动模型，假设某空间点p经过一次变换T(对应李代数为ξ)，得到 Tp 。现在，给T左乘一个扰△T=exp(δξ^ ),我们设扰动项的李代数为 δξ=[δρ,δφ]^T ,那么：

  把最后的结果定义成一个算符⊙，它把一个齐次坐标的空间点变换成一个 4*6 的矩阵。此式稍微需要解释的是矩阵求导方面的顺序，假设a,b,x,y都是列向量，那么在我们的符号
写法下，有如下的规则：

例子：评估轨迹的误差

  误差指标可以有很多种，常见的有绝对轨迹误差(AbsoluteTrajectoryError,ATE),形如：

  这实际上是每个位姿李代数的均方根误差(Root-Mean-SquaredError,RMSE)。这种误差可以刻
画两条轨迹的旋转和平移误差。同时，也有的文献仅考虑平移误差，从而可以定义绝对平移误差(Average Translational Error ):

  其中trans表示取括号内部变量的平移部分。因为从整条轨迹上看，旋转出现误差后，随后的轨迹在平移上也会出现误差，所以两种指标在实际中都适用。
  除此之外，也可以定义相对的误差。例如，考虑i时刻到 i+Δt 时刻的运动，那么相对位姿误差(Relative Pose Error,RPE)可定义为

  同样地，也可只取平移部分

四、似变换群与李代数

  如果在单目SLAM中使用SE(3)表示位姿，那么由于尺度不确定性与尺度漂移，整个SLAM过程中的尺度会发生变化，这在SE(3)中未能体现出来。因此，在单目情况下我们一般会显式地把尺度因子表达出来。用数学语言来说，对于位于空间的点p,在相机坐标系下要经过一个相似变换，而非欧氏变换：

  与SO(3)、SE(3)相似，相似变换也对矩阵乘法构成群，称为相似变换群Sim(3):

  同样地，Sim(3)也有对应的李代数、指数映射、对数映射等。李代数sim(3)元素是一个7维向量。它的前6维与se(3)相同，最后多了一项。

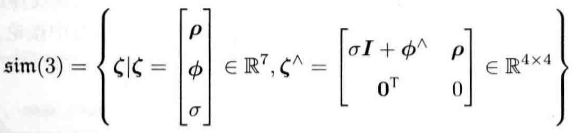
  它比se(3)多了一项。关联Sim(3)和 sin(3) 的仍是指数映射和对数映射。指数映射为

  其中，Js的形式为

  通过指数映射，我们能够找到李代数与李群的关系。对于李代数，它与李群的对应关系为

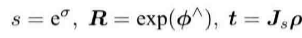
  转部分和SO(3)是一致的。平移部分，在se(3)中需要乘一个雅可比，而相似变换的雅可比更复杂。对于尺度因子，可以看到李群中的s即为李代数中的指数函数。
  一个点p经过相似变换Sp后，相对于S的导数，存在微分模型和扰动模型两种方式，而扰动模型较为简单。设给予Sp左侧一个小扰动exp(),并求Sp对于扰动的导数。因为Sp是4维的齐次坐标，ζ是7维向量，所以该导数应该是 4*7 的雅可比。方便起见，记Sp的前3维组成向量为q,那么：