为什么讲李群与李代数?要解决李群上只有乘法没有加法的问题,没法定义导数(没办法对旋转矩阵和变换矩阵做加法,令这个加法趋于0)。引入李代数之后就有了求导的途径。
目录
2.3 SO(3),SE(3),so(3),se(3)的对应关系
6、代码运行踩坑记录(slambook与slambook2)
0、引入
三维旋转矩阵构成了特殊正交群SO(3),变换矩阵构成了特殊欧式群SE(3)。两者对加法不封闭,对乘法是封闭的。
特殊正交群:
特殊欧式群:
1、李群与李代数基础
1.1 李群
- 群是一种集合加上一种运算的代数结构。群记作G=(A,▪)。群要求这个运算满足以下四个条件(封结幺逆)
- 封闭性:
- 结合律:
- 幺元:
- 逆:
- 封闭性:
- 旋转矩阵集合和矩阵乘法构成群;同样变换矩阵集合和矩阵乘法构成群。
- 李群是指具有连续(光滑)性质的群。像整数群那样离散的群没有连续性质,因此不是李群。而SO(n),SE(n)在实数空间上是连续的,能够直观想象一个刚体能够连续地在空间中运动,所以它们都是李群。
1.2 李代数的引出
- 对于任意旋转矩阵R,满足
,R是某个相机的旋转,随时间连续变化,即为时间的函数R(t)。可以推导出在t=0附近:
,进而推导出
- 由于仍然是旋转矩阵,有
,对两边求导得到
,整理得:
- 可以看出
是一个反对称矩阵,我们可以找到一个三维向量
与之对应:
- 上式两边右乘R(t)得到:
- 可以看出,每对旋转矩阵求一次导数,只需左乘一个
矩阵即可。
- 将R(t)在t=0附近进行泰勒展开:
- 可以看到
反映了R的导数性质,故称它在SO(3)原点附近的正切空间上。同时在
附近,设
保持为常数
,因此在
附近有
- 上式是一个关于R的微分方程,而且有初始值R(0)=I,求解得:
- 由于仍然是旋转矩阵,有
- 因此,在t=0附近,旋转矩阵可以由
计算出来。
- 我们可以看到,旋转矩阵R与另一个反对称矩阵
通过指数关系发生了联系,但是矩阵的指数是什么?这里有两点需要注意:
- 给定某时刻的R,我们就能求得一个
,它描述了R在局部的导数关系。与R对应的
有什么含义呢?
正是对应到SO(3)上的李代数so(3)。
- 给定某个向量
时,矩阵指数
如何计算?反之给定R,能否有相反的运算来计算
?事实上,这正是李群与李代数间的指数/对数映射。
- 给定某时刻的R,我们就能求得一个
1.3 李代数的定义
- 每个李群都有与之对应的李代数。李代数描述了李群的局部性质,准确来说,是单位元附近的正切空间。
- 李代数由一个集合
,一个数域
和一个二元运算[,]组成。如果它们满足以下性质,则称(
)为一个李代数,记作
。
- 封闭性
- 双线性
- 自反性:
。李代数要求元素与自己做李括号之后为零。
- 雅可比等价
- 示例:三维向量上定义的叉积是一种李括号,因此
构成了一个李代数。
1.4 李代数so(3)
- 第二章提到的
,事实上是一种李代数。SO(3)对应的李代数是定义在
上的向量,我们记作
。
- 在此定义下,两个向量
的李括号:
。(
代表从矩阵到向量)
- 由于向量
与反对称矩阵是一一对应的,在不引起歧义的情况下,就说
的元素是三维向量或者三维反对称矩阵,不加区别:
的内容,它们是一个由三维向量组成的集合,每个向量对应一个反对称矩阵,可以用于表达旋转矩阵的导数。它与SO(3)的关系由指数映射给定:
1.5 李代数se(3)
- SE(3)对应的李代数
位于
空间中:
元素记作
,是一个六维向量。前三维是平移,后三维是旋转。
- ^指代从向量到矩阵,
代表从矩阵到向量
不直接是平移
- 李代数
的李括号:
2、指数与对数映射
2.1 so(3)上的指数映射
- 如何计算
,这是一个矩阵的指数,在李群与李代数中,成为指数映射
- 任意矩阵A的指数映射可以写成一个泰勒展开(只在收敛的情况下有结果,结果仍是矩阵):
。
- 因此,
,推导可得:
是三维向量,可以定义它的模长和方向。
,这里
是一个长度为1的方向向量。
- 对于
,有以下两个性质:
,
- 结合以上2个性质,以及
、
的泰勒展开形式进行推导,最终可得
- 上式与罗德里格斯公式一致。so(3) 实际上就是所谓的旋转向量组成的空间,而指数映射即罗德里格斯公式。
- 通过指数映射(罗德里格斯公式),可以把so(3)中任意一个向量对应到一个位于SO(3)的旋转矩阵。
- 反之如果定义对数映射,也能把SO(3)中的元素对应到so(3)中:
。与指数映射一样,可以利用迹的性质分别求解转交和转轴。
- 如果把旋转角度规定在-180到180,那么李群和李代数元素是一一对应。
- 通过指数映射,旋转矩阵的导数可以由旋转向量指定,指导着如何在旋转矩阵中进行微积分运算。
2.2 se(3)上的指数映射
略
2.3 SO(3),SE(3),so(3),se(3)的对应关系

3、李代数求导与扰动模型
- 通过BCH线性近似,可以定义李代数的导数,进而可以推导so(3)和se(3)上的导数和扰动模型。
- 考虑一个基本问题:旋转后的点关于旋转的导数,不严谨地记为:
,由于R没有加法,导数无从定义。
- 存在两种解决办法:
- 对R对应的李代数加上小量,求相对于小量的变化率(导数模型)
- 对R左乘或右乘一个小量,求相对于小量的李代数的变化率(扰动模型)
- 通常扰动模型比导数模型更简洁。
4、实践:Sophus
5、涉及公式
- f(x)在点a的泰勒展开一般形式:
- exp(x)在x=0的泰勒展开:
6、代码运行踩坑记录(slambook与slambook2)
- slambook
- 安装第三方库Sophus时,cmake .. 时,报警告,无需担心,不影响后面编译使用。
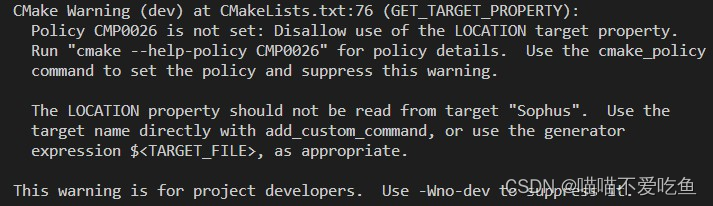
- make 报错。
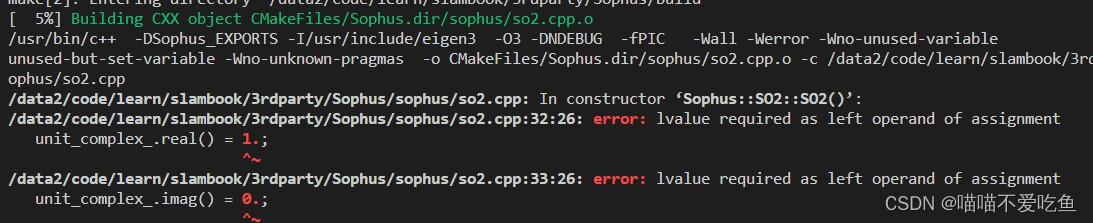
-
参考网上方法解决,如下图所示。
-
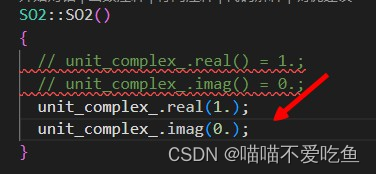
- 安装第三方库Sophus时,cmake .. 时,报警告,无需担心,不影响后面编译使用。
- slambook2
- Sophus 下载最新版本安装时,报错:CMake 3.24 or higher is required. You are running version 3.10.2。 但是使用ubuntu18.04 安装cmake版本就是3.10,怕冒然自己升级有问题。因此下载了Sophus 1.22.10 安装。
- 安装第三方库Sophus编译报错
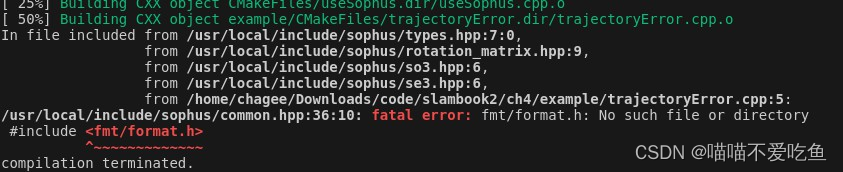
- 解决方法:参考网友方法,安装fmt解决。
- 安装之后sophous不报错,但编译ch4代码时报以下错误
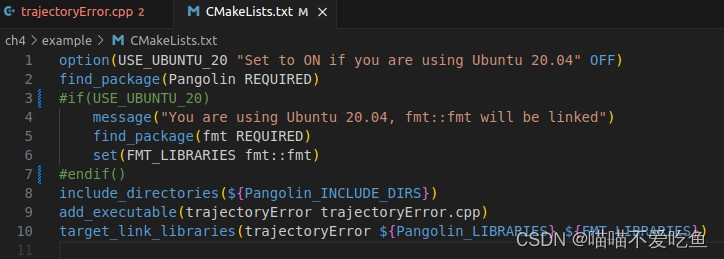
- 解决方法:引入fmt lib库























 874
874

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








