多元时间序列预测之（一）DA-RNN模型

前言

多元时间序列预测，又称多变量时间预测，指对一个系统中存在的多个时间依赖变量的研究。通常，我们假设系统中的这些变量存在相互依赖关系，即每个变量的未来值不仅于其历史值有关，还与其他变量的历史值有关。

多元时间序列存在于日常生活的方方面面，包括股票市场中不同股票的价格序列、不同道路的拥堵程度、不同城市的温度和降雨。从多变量时间序列中挖掘有意义的隐藏信息，并预测时间序列的未来趋势，可以造福于如金融、交通和天气预报等诸多社会领域。

本系列将以“多元时间序列预测”为目标，讲述深度学习领域在该系列的研究现状，对相关模型及其代码做详细解读，代码基于Pytorch实现。

DA-RNN论文解读

本文作为第一讲，将讲解多元时间序列预测任务的前身：基于外源性驱动序列的单时间序列预测。时间比较紧迫的同学可以跳过这一节，从下一节开始正式入门多元时间序列预测模型。

本节基于论文：A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction 基于注意力的双阶段递归神经网络模型。

1. 问题定义

首先，该模型属于NARX模型（The Nonlinear autoregressive exogenous model），即非线性的、外源性的自回归模型，这种模型基于当前时间序列的历史值和外源序列的（当前值）和历史值，对当前时间序列的未来值进行预测。

举个例子就是，假设我们现在要预测股票A的价格，那么我们只看A的历史价格可能是不够的，我们还需看股票A的交易量、股票A的换手率、甚至和股票A相关的股票B的价格，我们称股票A的价格序列为目标序列，其他和股票A的价格序列相关的序列为外源序列，我们需要结合外源序列所具有的信息来对目标序列进行预测。

在以往的NARX模型，很少有人能够适当地捕捉长期的时间依赖关系，并选择相关的外源系列来进行预测。DARNN便是用来解决这两个问题。
对于NARX建模，其目标是使用DA-RNN来近似函数$F(\cdot )$，以便通过观察所有输入和模型内的输出来获得目标序列在时间T的估计值，其公式被设计为：
$${\hat{y}}_T=F(y_1,y_2,...,y_{T-1},X_1,X_2,...,X_{T-1})$$
注，这里与原文稍有差别，原文中在时间$T$处可以得知驱动序列$X_T$的值，我们认为，大多数情况下，该值应该是未知的，因此应该在时间$T$仅知目标序列$y_{T-1}$和驱动序列$X_{T-1}$的值。

2. 模型解读

DA-RNN模型使用基于注意力机制的编码器-解码器思想框架。在编码器中，引入了一种新的输入注意力机制，它可以自适应地选择相关的驱动序列；在解码器中，使用时间注意机制在所有时间步长中自动选择相关的编码器隐藏状态。利用这两种注意机制，DA-RNN可以自适应地选择最相关的输入特征，并捕获一个时间序列的长期时间依赖性。模型整体框架如下所示：

接下来，我们将对其进行分块解读。

2.1 输入注意力机制

输入注意力机制用来对在时刻$a$上可以观测到的多条驱动序列$X(a)\in R^{n\times T}$进行特征提取，融合成新的输入特征。其结构如下图所示：

给定第k个驱动序列$X^k=(x_1^k,x_2^k,...x_T^k)\in R^T$，其注意力系数计算方式如下：
$$e_t^k=v_e^{\top }tanh(W_e[h_{t-1};s_{t-1}]+U_e{X}^k)$$
并有，
$${\alpha }_t^k=\frac{exp(e_t^k)}{{\sum }_{i=1}^{n}exp(e_t^i)}$$

讲解一下这个公式的思路，首先$h_{t-1}$和$s_{t-1}$是LSTM模块的隐藏状态和单元状态，通过$[;]$做矩阵拼接运算，这个下一节中讲解，现在可以直接理解为序列模型在时间$t$所具有的某种隐藏状态，注意力系数的计算目的就是计算$X^k$和这种隐藏状态的相关性权重$e_t^k$，然后经过softmax归一化，得到最终的相关性系数${\alpha }_t^k$。其他参数矩阵，均为可训练参数。

其中，矩阵相关性的计算方式有很多，现有的模型中，大都使用的是另一种方法——矩阵点乘。通过矩阵点乘的结果衡量两矩阵相关性，这也是当今主流的transform中使用的方法，而在本文这种采用的是先对矩阵做线性变换，然后相加再使用tanh激活函数。有兴趣的可以再自行深入研究不同的矩阵相关性的计算方法有何差别。

有了注意力系数，我们就可以以此为权重，对驱动序列进行合成，得到驱动序列在时间$t$处的具有空间关系的特征向量：
$${\tilde{X}}_t=({\alpha }_t^1{X}_t^1,{\alpha }_t^2{X}_t^2,...,{\alpha }_t^n{X}_t^n{)}^{\top }$$

2.2 编码器

编码器的目的是获取时间序列在$[1,T]$的各个时间点$t$处的隐藏特征，由于时间序列的时序特性，本模型使用LSTM模块进行时序特征提取。
但是需要注意的是，这里的输入序列是什么呢？并不是我们想要预测的目标序列，而是我们前一节中新合成的驱动序列，即根据注意力系数得到的考虑了空间关系的合成驱动序列$\tilde{X}$。其结构如下图所示：

应用LSTM模块提取其时序特征：
$$h_t=f_{lstm1}(h_{t-1},{\tilde{X}}_{t-1})$$
LSTM模块的相关公式比较基础，这里不再赘述。

值得一提的是，这里LSTM迭代过程中每个时间$t$的隐藏状态，不仅仅会作为输出和下一层迭代的输入，也会传递给下一层的输入注意力机制，用于构建${\tilde{X}}_t$（上一节中提到的$h_{t-1}$和$s_{t-1}$）。

输入注意力机制+编码器的目的，简单来说就是通过LSTM提取驱动序列间考虑了空间关系的时序特征。通过所提出的输入注意机制，编码器可以选择性地关注特定的驱动序列，而不是平等地处理所有的输入驱动序列。

2.3 时间注意力层

当我们在时间$a$处，获得了合成序列$\tilde{X}\in R^T$，为提取其时序特征，简单的做法是直接通过LSTM模型，输出其最后一个隐藏特征$h_T$。但本文并未如此做，而是试图通过注意力机制，将$[1,T]$的各个时间点的隐藏状态$h_t$进行加权，从而提取到回看序列中较为重要的隐藏状态。该部分结构如下图所示：

注意力系数的计算方式与输入注意力机制相同，即：
$$l_t^k=v_d^{\top }tanh(W_d[d_{t-1};s_{t-1}^{\prime }]+U_d{X}^i),1\le i\le T$$
并有，
$${\beta }_t^i=\frac{exp(e_t^i)}{{\sum }_{j=1}^{T}exp(e_t^j)}$$
其中的$d_{t-1}$和$s_{t-1}^{\prime }$是下一节中的LSTM模块的隐藏状态和单元状态。
通过注意力系数，我们可以计算考虑了注意力权重的、新的驱动序列在时间$t$的隐藏状态特征：
$$c_t=\sum _{i=1}^T{\beta }_t^i{h}_i$$

2.4 解码器

该模块本质就是一个LSTM，如下图所示：

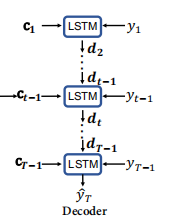
在时间$a-1$处,我们将驱动序列特征与标的序列$y_{a-1}$进行拼接，可得到最终的时间序列值：
$${\hat{y}}_{a-1}={\tilde{W}}^{\top }[y_{a-1};c_{a-1}]+\tilde{b}$$
再将最终时间序列$\hat{y}$输入另一个LSTM模块，以提取其的时序特征：
$$d_a=f_{lstm2}(d_{a-1},{\tilde{y}}_{a-1})$$
通过LSTM模型中的隐藏状态$d_a$和$c_a$，我们给出模块在时间$a$处的最终输出：
$${\hat{y}}_a=v_y^{\top }(W_y[d_a;c_a]+b_w)+b_v$$

总得来说，该模型将时间$a$处获得的长度为$T$的多条驱动序列作为一个信息矩阵，通过输入注意力机制、编码器、时间注意力层进行特征提取，使其变为特征向量$c_a$，再将其与目标序列$y_a$进行拼接，即可得到最终合成的时间序列，然后再使用一个LSTM模型对此最终时间序列进行时序预测，便得到考虑了驱动序列信息的时间序列预测结果。