卡尔曼滤波器
首先要特别感谢B站的UP主DR_CAN,本文的公式推导都来自他的:【卡尔曼滤波器】_DR_CAN合集以及书籍:控制之美,侵删。感兴趣的同学可以移步B站。本文将结合视频和书籍,尽可能详尽的完成卡尔曼滤波器的公式推导。
0.如果你想知道卡尔曼滤波器处于控制理论的什么位置
这一部分会简单介绍一下自动控制理论的发展(摘自卢京潮:自动控制原理),其实只需要通过简单的时间节点就能够帮助大家理清自动化专业所学的那些课程之间的脉络体系,让大家对自动控制理论、现代控制理论、以及卡尔曼滤波器之间的关系有一个大概的认识。
经典控制理论:
- 1788年,英国人瓦特(James Watt) 在他发明的蒸汽机上使用了离心调速器,解决了蒸汽机的速度控制问题。但是时候人们曾经试图改善调速器的准确性,却常常导致系统产生振荡。
- 1868年,英国物理学家麦克斯韦通过对调速系统线性常微分方程的建立和分析,解决了瓦特控制系统中出现的不稳定问题,开辟了用数学方法研究控制系统的途径。(线性常微分方程)
- 1877年和1895年,英国数学家劳斯和德国数学家赫尔维兹分别独立的建立了直接根据代数方程的系数判别系统稳定性的准则,这些方法奠定了经典控制理论中时域分析方法的基础。(劳斯判据、赫尔维兹稳定判据)
- 1932年,美国物理学家奈奎斯特研究了研究了长距离电话线信号传输中出现失真的问题,运用复变函数理论建立了以频率特性为基础的稳定判据,奠定了频率响应法的基础。随后,伯德和尼科尔斯在20世纪30年代末和40年代初进一步将频率响应法加以发展,形成了经典控制理论的频域分析法。(奈奎斯特稳定判据、伯德图、尼科尔斯图)
- 1948年,美国科学家伊万斯创立了根轨迹方法。(根轨迹)
以传递函数最为描述系统的数学模型,以时域分析法、根轨迹法和频域分析方法为主要分析工具,构成了经典控制理论的基本框架。到20世纪50年代,经典控制理论发展到相当成熟的地步,形成了相对完整的理论体系。
经典控制理论研究的对象基本上是以线性定常系统为主的单输入-单输出系统。
现代控制理论:
- 20世纪50年代中期,空间技术的发展迫切要求解决更复杂的多变量系统、非线性系统的最优控制问题。同时,计算机技术的发展也从计算手段上为控制理论的发展提供了条件。适合于航天器的运动规律、又便于计算机求解的状态空间描述成为主要的模型形式。(状态空间描述)
- 1892年,俄国数学家李雅普诺夫创立稳定性理论。(李雅普诺夫稳定性判别法)
- 1956年,前苏联科学见庞特里亚金提出极大值原理。(极大值原理)
- 1956年,美国数学家贝尔曼创立了动态规划。(动态规划)
- 1959年,美国数学家卡尔曼提出了著名的卡尔曼滤波算法。(卡尔曼滤波器)
- 1960年,贝尔曼提出系统的可控性和可观测性问题。(可控性和可观测性)
到20世纪60年代初,一套以状态方程作为描述系统的数学模型,以最优控制和卡尔曼滤波为核心控制系统分析设计的新原理和方法基本确定,现代控制理论应运而生,它适用于多变量、非线性、时变系统。
智能控制理论:
为了解决现代控制理论在工业生产过程应用中所遇到的被控对象精确状态空间模型不易建立,合适的最优性能指标难以构造,所得最优控制器往往过于复杂等问题,近几十年中不断提出一些新的控制方法和理论,例如:自适应控制、预测控制、容错控制、鲁棒控制、非线性控制等等,大大地扩展了控制理论的研究范围。以控制论、信息论、仿生学为基础的只能控制理论,开拓了更广泛的研究领域,在信息与控制学科研究中注入了蓬勃的生命力。
温馨提示:由上面的控制理论发展介绍可以看出,阅读本文你需要理解现代控制理论的状态方程的概念。
1.什么是卡尔曼滤波器?
卡尔曼滤波器是一种最优化的、递归的、数字处理的算法。它兼具滤波器和观测器的特性。在某些应用中,卡尔曼滤波器主要用于对系统状态的估计和预测,因此被视为状态观测器;在其他应用种,卡尔曼滤波器主要用于对噪声信号的滤波和去噪,因此被视为信号滤波器。
卡尔曼滤波器通过将多个传感器或测量器的数据进行融合,利用概率论和线性系统理论对状态进行估计和预测,它能够根据先验知识和测量信息来递归地更新状态估计,并提供对未来状态的最优预测。
如果你对上面一段话中的数据融合、先验知识,递归更新,最优预测等等存在疑问或者没有概念,没有关系,我们可以接着往下看。在你读完这篇文章之后,我希望你可以再次回来重新看这一段话,如果你看懂了卡尔曼滤波器,那么你就可以完全读懂这一段,明白它怎样递归,以及为什么是最优的。
1.1什么是递归算法和数据融合?
首先我们要来学习一下什么是数据融合。
如图1所示,一台无人机使用压力传感器来测量飞行的高度,我们用
Z
k
{Z_k}
Zk表示测量结果,下标
k
{k}
k 代表第
k
{k}
k 次测量,我们假设一共进行了
k
{k}
k次测量,并将每次的测量结果记为:
Z
1
{Z_1}
Z1、
Z
2
{Z_2}
Z2、
Z
3
{Z_3}
Z3…
Z
k
{Z_k}
Zk。

因为在实际测量中,由于测量过程中存在随机误差,所以每次测量的结果都会有所不同。那么我们怎么估计无人机飞行的真正高度呢?很顺理成章的一个想法就是,我们对这些测量值求平均值。即:
Z
^
k
=
1
k
(
z
1
+
z
2
+
⋯
+
z
k
)
(1)
{\hat Z_k} = \frac{1}{k}({z_1} + {z_2} + \cdots + {z_k}) \tag{1}
Z^k=k1(z1+z2+⋯+zk)(1)
其中,
Z
^
k
{\hat Z_k}
Z^k就是经过次测量后的估计值,
∧
\wedge
∧代表估计,(也就是我们根据测量值求出来的平均值,并不是无人机飞行的真实值)。
这个求平均值的方法是我们在日常生活中最常用的方法,但是这个方法存在两个缺陷:
1.每一次运算都需要做
k
{k}
k次加法运算和1次乘法运算,随着
k
{k}
k的增加,加法的计算量会逐步增大。
2.每一次的测量结果都需要保留,也就是说如果进行
k
{k}
k次测量,那么就需要存储
k
{k}
k次结果,非常占用存储空间。
那么我们可以对公式(1)进行一点简单的运算,将
Z
k
{Z_k}
Zk提出来,得到:
Z
^
k
=
1
k
(
z
1
+
z
2
+
⋯
+
z
k
)
=
1
k
(
z
1
+
z
2
+
⋯
+
z
k
−
1
)
+
1
k
z
k
=
k
−
1
k
[
1
k
−
1
(
z
1
+
z
2
+
⋯
+
z
k
−
1
)
]
+
1
k
z
k
(2)
\begin{aligned} {{\hat Z}_k} &= \frac{1}{k}({z_1} + {z_2} + \cdots + {z_k})\\ &= \frac{1}{k}({z_1} + {z_2} + \cdots + {z_{k - 1}}) +\textcolor{#FF0000}{ \frac{1}{k}{z_k}}\\\\ &= \frac{{k - 1}}{k}[\textcolor{#FF0000}{\frac{1}{{k - 1}}({z_1} + {z_2} + \cdots + {z_{k - 1}})}] + \frac{1}{k}{z_k} \tag{2} \end{aligned}
Z^k=k1(z1+z2+⋯+zk)=k1(z1+z2+⋯+zk−1)+k1zk=kk−1[k−11(z1+z2+⋯+zk−1)]+k1zk(2)
其中,
1
k
−
1
(
z
1
+
z
2
+
⋯
+
z
k
−
1
)
=
z
^
k
−
1
\frac{1}{{k - 1}}({z_1} + {z_2} + \cdots + {z_{k - 1}}) = {\hat z_{k - 1}}
k−11(z1+z2+⋯+zk−1)=z^k−1是
k
−
1
{k-1}
k−1次测量后的平均值,带入公式(2)化简,可得:
z
^
k
=
k
−
1
k
z
^
k
−
1
+
1
k
z
k
=
z
^
k
−
1
−
1
k
z
^
k
−
1
+
1
k
z
k
=
z
^
k
−
1
+
1
k
(
z
k
−
z
^
k
−
1
)
(3)
\begin{aligned} \textcolor{#FF0000}{{{\hat z}_k}} &= \frac{{k - 1}}{k}{{\hat z}_{k - 1}} + \frac{1}{k}{z_k}\\ & = {{\hat z}_{k - 1}} - \frac{1}{k}{{\hat z}_{k - 1}} + \frac{1}{k}{z_k}\\ & = {\textcolor{#FF0000}{ {\hat z}_{k - 1}}} + \frac{1}{k}({z_k} - \textcolor{#FF0000}{{{\hat z}_{k - 1}}}) \tag{3} \end{aligned}
z^k=kk−1z^k−1+k1zk=z^k−1−k1z^k−1+k1zk=z^k−1+k1(zk−z^k−1)(3)
公式(3)就是公式(1)的另一种表达形式。
对比公式(1)和(3),我们可以发现,公式(3)只需要进行两次加法运算和一次乘法运算;并且,在每一次运算之后只需要保留上一次的估计值,即: z ^ k − 1 {\hat z_{k - 1}} z^k−1和当前次数 k {k} k,这将大大减少硬件存储空间的使用。这种通过上一次估计值( z ^ k − 1 {\hat z_{k - 1}} z^k−1)推断当前估计值( z ^ k {\hat z_{k}} z^k)的算法被称为递归算法。
观察公式(3),当测量值
k
{k}
k很大时,
1
k
≈
0
\frac{1}{k} \approx 0
k1≈0,
z
^
k
≈
z
^
k
−
1
{\hat z_k} \approx {\hat z_{k - 1}}
z^k≈z^k−1,新的测量结果对估计值的影响就很小。反之,当
k
{k}
k很小时,测量值与上一次的估计值之间的差就会对新的估计值产生较大的影响。定义公式(3)中的
1
k
\frac{1}{k}
k1
Δ
=
\Delta \over =
=Δ
K
k
{K_k}
Kk ,那么公式(3)可以写成:
z
^
k
=
z
^
k
−
1
+
K
k
(
z
k
−
z
^
k
−
1
)
(4)
\textcolor{#FF0000}{{\hat z_k} = {\hat z_{k - 1}} + {K_k}({z_k} - {\hat z_{k - 1}})} \tag{4}
z^k=z^k−1+Kk(zk−z^k−1)(4)
此时
K
k
{K_k}
Kk是一个调整系数,在本例中
K
k
∈
[
0
,
1
]
{K_k} \in [0,1]
Kk∈[0,1],且随着
k
{k}
k的增加而减小。公式(4)体现了数据融合的思想,通过调整系数将测量值与上一次的估计值融合在一起。
注:公式(4)是不是与卡尔曼滤波器的公式4非常相似?
卡尔曼滤波器公式4: x ^ k = x ˉ k + K ( z k − H x ˉ k ) {\hat x_k} = {\bar x_k} + {K}({z_k} - H{\bar x_k}) x^k=xˉk+K(zk−Hxˉk)
1.这个公式中的符号会在后文进行详细讲解;
2.有的同学可能会发现这个公式的形式也许和你在其他地方看见的形式略有差别,这只是符号表示或者是否进行变形的区别,看完后文,你会理解他们之间的异同。
数据融合意味着我们使用两个“不太准确”的结果融合出一个相对准确的估计值,这一思想在工程中有非常广泛的应用,使用多传感器融合可以有效地提高精度和可靠性。
数据融合的思想非常重要,它是推导卡尔曼滤波器的基础,请大家记住并深刻理解。
1.2概率论与协方差矩阵
卡尔曼滤波器是一种基于概率的计算方法,用于处理系统中的不确定性。从这一小节开始,到第二节我们会简单复习一下推导卡尔曼滤波器时,会用到的几个基本概念,如果你已经熟练掌握这些公式概念,可以直接跳转到第二节进行公式推导。
1.2.1概率、期望、方差、标准差
卡尔曼滤波器所研究的多为连续信号,因此涉及的随机变量也多为连续型随机变量。对于连续型随机变量
X
{X}
X,用
f
X
(
x
)
{f_X}(x)
fX(x)代表其概率密度函数,对其取定积分就可以得到随机变量
X
{X}
X在某一区间内的概率。例如,
a
≤
X
≤
b
a \le X \le b
a≤X≤b的概率为:
P
(
a
≤
X
≤
b
)
=
∫
a
b
f
X
(
x
)
d
x
P(a \le X \le b) = \int_a^b {{f_X}(x)dx}
P(a≤X≤b)=∫abfX(x)dx
随机变量
X
{X}
X的期望定义为:
E
(
X
)
=
∫
−
∞
+
∞
x
f
X
(
x
)
d
x
(5)
E(X) = \int_{ - \infty }^{ + \infty } {x{f_X}(x)dx} \tag{5}
E(X)=∫−∞+∞xfX(x)dx(5)
它代表了对随机变量的数值进行平均运算。期望运算是线性运算,存在以下几个重要性质:
E
(
a
)
=
a
,
a
为常数
E
(
a
X
)
=
a
E
(
X
)
,
a
为常数
E
(
X
+
Y
)
=
E
(
X
)
+
E
(
Y
)
,
X
、
Y
是两个随机变量
E
(
X
Y
)
=
E
(
X
)
E
(
Y
)
,
X
、
Y
是两个相互独立的随机变量
(6)
\begin{array}{l} E(a) = a,a为常数\\\\ E(aX) = aE(X),a为常数\\\\ E(X + Y) = E(X) + E(Y),X、Y是两个随机变量\\\\ \textcolor{#FF0000}{E(XY) = E(X)E(Y),X、Y是两个相互独立的随机变量} \tag{6} \end{array}
E(a)=a,a为常数E(aX)=aE(X),a为常数E(X+Y)=E(X)+E(Y),X、Y是两个随机变量E(XY)=E(X)E(Y),X、Y是两个相互独立的随机变量(6)
温馨提示:标红的公式在后文推导中会用到,请读者阅读时稍加留意。
随机变量
X
{X}
X的方差被定义为:
V
a
r
(
X
)
=
∫
−
∞
+
∞
(
X
−
E
(
X
)
)
2
f
X
(
x
)
d
x
(7)
Var(X) = \int_{ - \infty }^{ + \infty } {{{(X - E(X))}^2}{f_X}(x)dx} \tag{7}
Var(X)=∫−∞+∞(X−E(X))2fX(x)dx(7)
根据公式(5)和(7)可以发现,
X
{X}
X的方差就是
(
X
−
E
(
X
)
)
2
{{(X - E(X))}^2}
(X−E(X))2的期望,即:
V
a
r
(
X
)
=
E
(
(
X
−
E
(
X
)
)
2
)
(8)
Var(X) = E({(X - E(X))^2}) \tag{8}
Var(X)=E((X−E(X))2)(8)
因此,方差描述了随机变量
X
{X}
X的离散程度
X
−
E
(
X
)
{X - E(X)}
X−E(X)的平均值嘛),方差小意味着堆积变量的概率密度集中在期望
E
(
X
)
{E(X)}
E(X)附近,反之亦然。
根据公式(6)将公式(8)展开得:
V
a
r
(
X
)
=
E
(
(
X
−
E
(
X
)
)
2
)
=
E
(
(
X
−
E
(
X
)
)
(
X
−
E
(
X
)
)
)
=
E
(
X
2
−
2
X
E
(
X
)
+
E
(
X
)
2
)
=
E
(
X
2
)
−
2
E
(
X
E
(
X
)
)
+
E
(
X
)
2
=
E
(
X
2
)
−
2
E
(
X
)
E
(
X
)
+
E
(
X
)
2
=
E
(
X
2
)
−
2
E
(
X
)
E
(
X
)
+
E
(
X
)
E
(
X
)
=
E
(
X
2
)
−
E
(
X
)
2
(9)
\begin{aligned} \textcolor{#FF0000}{Var(X) }&= E({(X - E(X))^2})\\ &= E((X - E(X))(X - E(X)))\\ &= E({X^2} - 2XE(X) + E{(X)^2})\\ &= E({X^2}) - 2E(XE(X)) + E{(X)^2}\\ &= E({X^2}) - 2E(X)E(X) + E{(X)^2}\\ &= E({X^2}) - 2E(X)E(X) + E(X)E(X)\\ &= \textcolor{#FF0000}{E({X^2}) - E{(X)^2}} \tag{9} \end{aligned}
Var(X)=E((X−E(X))2)=E((X−E(X))(X−E(X)))=E(X2−2XE(X)+E(X)2)=E(X2)−2E(XE(X))+E(X)2=E(X2)−2E(X)E(X)+E(X)2=E(X2)−2E(X)E(X)+E(X)E(X)=E(X2)−E(X)2(9)
方差的性质有:
V
a
r
(
a
)
=
0
,
a
为常数
V
a
r
(
a
X
)
=
a
2
V
a
r
(
X
)
,
a
为常数
V
a
r
(
X
+
Y
)
=
V
a
r
(
X
)
+
2
E
(
X
−
E
(
X
)
)
(
Y
−
E
(
Y
)
)
+
V
a
r
(
Y
)
,
X
、
Y
是两个随机变量
V
a
r
(
X
+
Y
)
=
V
a
r
(
X
)
+
V
a
r
(
Y
)
,
X
、
Y
是两个相互独立的随机变量
(10)
\begin{array}{l} Var(a) = 0,a为常数\\\\ Var(aX) = {a^2}Var(X),a为常数\\\\ Var(X + Y) = Var(X) + 2E(X - E(X))(Y - E(Y)) + Var(Y),X、Y是两个随机变量\\\\ \textcolor{#FF0000}{Var(X + Y) = Var(X) + Var(Y),X、Y是两个相互独立的随机变量} \tag{10} \end{array}
Var(a)=0,a为常数Var(aX)=a2Var(X),a为常数Var(X+Y)=Var(X)+2E(X−E(X))(Y−E(Y))+Var(Y),X、Y是两个随机变量Var(X+Y)=Var(X)+Var(Y),X、Y是两个相互独立的随机变量(10)
标准差是方差的算数平方根,定义为
σ
X
=
V
a
r
(
X
)
{\sigma _X} = \sqrt {Var(X)}
σX=Var(X) ,因此
X
{X}
X的方差也可以写成
V
a
r
(
X
)
=
σ
X
2
Var(X) = \sigma _X^2
Var(X)=σX2
1.2.2正态分布
正态分布也称为高斯分布,大部分随机过程中产生的误差都服从或者接近于正态分布。
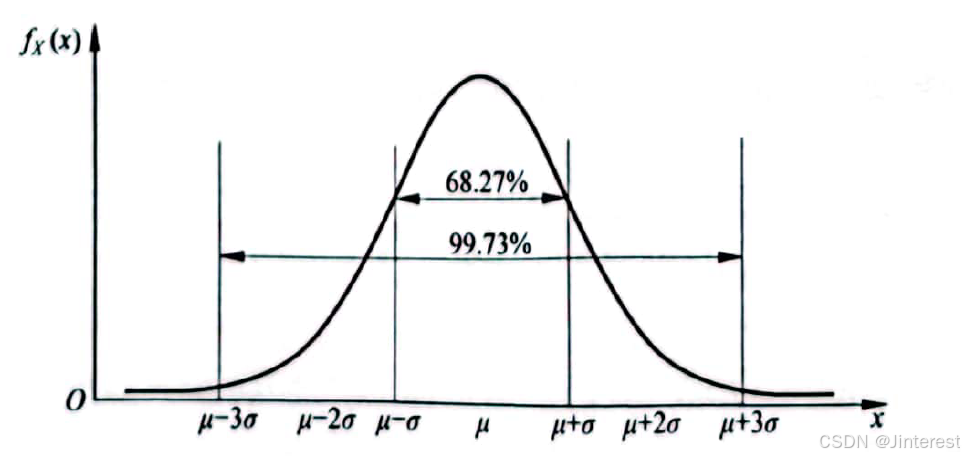
如果一个随机变量 X {X} X服从正态分布,它可以表达为 X ∼ N ( μ , σ 2 ) \textcolor{#FF0000}{X \sim N(\mu ,{\sigma ^2})} X∼N(μ,σ2),其中 μ = E ( X ) \mu = E(X) μ=E(X)代表期望, σ 2 = V a r ( X ) {\sigma ^2} = Var(X) σ2=Var(X)代表方差。
在正态分布下,一个标准差带宽内
(
μ
±
σ
)
(\mu \pm \sigma )
(μ±σ)的概率为68.27%,在三个标准差带宽内
(
μ
±
3
σ
)
(\mu \pm 3\sigma )
(μ±3σ)的概率为99.73%,通过计算数据的均值和标准差,我们可以了解变量的集中趋势和离散程度。
其概率密度为:
f
X
(
x
)
=
1
2
π
σ
2
e
−
(
x
−
μ
)
2
2
σ
2
{f_X}(x) = \frac{1}{{\sqrt {2\pi {\sigma ^2}} }}{e^{ - \frac{{{{(x - \mu )}^2}}}{{2{\sigma ^2}}}}}
fX(x)=2πσ21e−2σ2(x−μ)2
1.2.2.1测量误差的数据融合案例
在工程中,测量误差会被考虑为正态分布。基于这一思想,可以将多个带有误差的测量数据融合在一起,得到一个相对准确的测量值。考虑在1.1小节中的无人机高度测量的例子,如果我们在气压计之外增加一个超声波传感器如图所示,假如通过气压计测得的高度
Z
1
=
50
m
{Z_1} = 50m
Z1=50m,通过超声波测得的高度
Z
2
=
52
m
{Z_2} = 52m
Z2=52m,下面我们将运用1.1中的数据融合思想科学地将两者融合在一起并得到一个理论上最优的估计值。

设想这两种传感器的测量精度完全一样,那么可以简单地取他们的平均值作为估计值,即,
Z
^
=
1
2
(
Z
1
+
Z
2
)
=
51
m
\hat Z = \frac{1}{2}({Z_1} + {Z_2}) = 51m
Z^=21(Z1+Z2)=51m(这里记得吗,我们前面说过
∧
\wedge
∧代表估计)。而在现实生活中,每一个传感器都有自己的精度范围,测量时产生的随机误差也不相同。定义这两个传感器的误差分别为:
e
1
=
Z
a
−
Z
1
e
2
=
Z
a
−
Z
2
\begin{array}{l} {e_1} = {Z_a} - {Z_1}\\ {e_2} = {Z_a} - {Z_2} \end{array}
e1=Za−Z1e2=Za−Z2
其中,
Z
a
{Z_a}
Za是无人机在
K
{K}
K时刻的真实高度值(下标a代表actual)。在本例中,我们假设气压计的测量误差服从正态分布
e
1
∼
N
(
0
,
σ
e
1
2
)
e_1 \sim N(0 ,{\sigma _{{e_1}}^2})
e1∼N(0,σe12),其中期望
E
(
e
1
)
=
0
E({e_1}) = 0
E(e1)=0,标准差
σ
e
1
=
1
m
{\sigma _{{e_1}}} = 1m
σe1=1m,当使用气压计的测量结果
Z
1
=
50
m
{Z_1} = 50m
Z1=50m时,其真实结果的概率分布如图所示:

同理,假设超声波传感器的测量误差服从正态分布
e
2
∼
N
(
0
,
σ
e
2
2
)
e_2 \sim N(0 ,{\sigma _{{e_2}}^2})
e2∼N(0,σe22),其中期望
E
(
e
2
)
=
0
E({e_2}) = 0
E(e2)=0,标准差
σ
e
2
=
0.5
m
{\sigma _{{e_2}}} = 0.5m
σe2=0.5m,当使用气压计的测量结果
Z
2
=
52
m
{Z_2} = 52m
Z2=52m时,其真实结果的概率分布如图所示:

由图可知,由于超声波传感器测量误差的标准差较小(
σ
e
2
<
σ
e
1
{\sigma _{{e_2}}} < {\sigma _{{e_1}}}
σe2<σe1),所以它在途中所形成的钟形曲线比气压计的曲线更加修长,真实值更大概率第集中在测量值
Z
2
=
52
m
{Z_2} = 52m
Z2=52m周围。
下一步就是将这两条曲线通过某种方式融合,形成一个误差标准差更小的估计值,根据1.1小节中的公式(4),一个通用的数据融合算法可以写成: Z ^ = Z 1 + K ( Z 2 − Z 1 ) \hat Z = {Z_1} + K({Z_2} - {Z_1}) Z^=Z1+K(Z2−Z1)其中, K ∈ [ 0 , 1 ] K \in [0,1] K∈[0,1]。
对于这个 K K K的取值,如果测量结果 Z 1 Z_1 Z1的精度远远高于 Z 2 Z_2 Z2(误差小,即 σ e 1 ≪ σ e 2 {\sigma _{{e_1}}} \ll {\sigma _{{e_2}}} σe1≪σe2),可以令参数 K = 0 K=0 K=0,此时的估计值 Z ^ = Z 1 \hat Z = {Z_1} Z^=Z1.相反,如果测量结果 Z 1 Z_1 Z1的精度远远低于 Z 2 Z_2 Z2( σ e 1 ≫ σ e 2 {\sigma _{{e_1}}} \gg {\sigma _{{e_2}}} σe1≫σe2),可令 K = 1 K=1 K=1,此时的估计值 Z ^ = Z 2 \hat Z = {Z_2} Z^=Z2.当 K = 0.5 K=0.5 K=0.5时,则取两者的平均值。
在本例中, σ e 2 < σ e 1 {\sigma _{{e_2}}} < {\sigma _{{e_1}}} σe2<σe1,所以 K K K的取值应该是一个大于0.5的数值,这会使得计算结果偏向于 Z 2 {Z_2} Z2。
为了求解最优的参数
K
K
K,定义估计误差为:
e
^
=
Z
a
−
Z
^
\hat e = {Z_a} - \hat Z
e^=Za−Z^那么根据公式,可得:
e
^
=
Z
a
−
Z
^
=
Z
a
−
(
Z
1
+
K
(
Z
2
−
Z
1
)
)
=
Z
a
−
Z
1
−
K
(
Z
2
−
Z
1
)
=
(
Z
a
−
Z
1
)
+
K
(
Z
1
−
Z
2
)
=
(
Z
a
−
Z
1
)
+
K
(
Z
1
−
Z
2
+
Z
a
−
Z
a
)
=
(
Z
a
−
Z
1
)
+
K
(
(
Z
a
−
Z
2
)
−
(
Z
a
−
Z
1
)
)
\begin{aligned} \hat e &= {Z_a} - \hat Z\\ &= {Z_a} - ({Z_1} + K({Z_2} - {Z_1}))\\ &= {Z_a} - {Z_1} - K({Z_2} - {Z_1})\\ &= ({Z_a} - {Z_1}) + K({Z_1} - {Z_2})\\ &= ({Z_a} - {Z_1}) + K({Z_1} - {Z_2} + {Z_a} - {Z_a})\\ &= ({Z_a} - {Z_1}) + K(({Z_a} - {Z_2}) - ({Z_a} - {Z_1})) \end{aligned}
e^=Za−Z^=Za−(Z1+K(Z2−Z1))=Za−Z1−K(Z2−Z1)=(Za−Z1)+K(Z1−Z2)=(Za−Z1)+K(Z1−Z2+Za−Za)=(Za−Z1)+K((Za−Z2)−(Za−Z1))又因为:
e
1
=
Z
a
−
Z
1
e
2
=
Z
a
−
Z
2
\begin{array}{l} {e_1} = {Z_a} - {Z_1}\\ {e_2} = {Z_a} - {Z_2}\\ \end{array}
e1=Za−Z1e2=Za−Z2所以:
e
^
=
e
1
+
K
(
e
2
−
e
1
)
\hat e = {e_1} + K({e_2} - {e_1})
e^=e1+K(e2−e1)又因为
E
(
e
1
)
=
E
(
e
2
)
=
0
E({e_1}) = E({e_2}) = 0
E(e1)=E(e2)=0,那么,估计误差的期望:
E
(
e
^
)
=
E
(
e
1
+
K
(
e
2
−
e
1
)
)
=
E
(
(
1
−
K
)
e
1
+
K
e
2
)
=
(
1
−
K
)
E
(
e
1
)
+
K
E
(
e
2
)
=
0
\begin{aligned} E(\hat e) &= E({e_1} + K({e_2} - {e_1}))\\ &= E((1 - K){e_1} + K{e_2})\\ &= (1 - K)E({e_1}) + KE({e_2}) = 0 \end{aligned}
E(e^)=E(e1+K(e2−e1))=E((1−K)e1+Ke2)=(1−K)E(e1)+KE(e2)=0估计误差的方差为:
σ
e
^
2
=
V
a
r
(
e
1
+
K
(
e
2
−
e
1
)
)
=
V
a
r
(
(
1
−
K
)
e
1
+
K
e
2
)
\begin{aligned} \sigma _{\hat e}^2 &= Var({e_1} + K({e_2} - {e_1}))\\ &= Var((1 - K){e_1} + K{e_2}) \end{aligned}
σe^2=Var(e1+K(e2−e1))=Var((1−K)e1+Ke2)由于这两次测量是相互独立的,根据方差运算性质可以写成:
σ
e
^
2
=
V
a
r
(
(
1
−
K
)
e
1
+
K
e
2
)
=
V
a
r
(
(
1
−
K
)
e
1
)
+
V
a
r
(
K
e
2
)
=
(
1
−
K
)
2
V
a
r
(
e
1
)
+
K
2
V
a
r
(
e
2
)
=
(
1
−
K
)
2
σ
e
1
2
+
K
2
σ
e
2
2
\begin{aligned} \sigma _{\hat e}^2 &= Var((1 - K){e_1} + K{e_2})\\ &= Var((1 - K){e_1}) + Var(K{e_2})\\ &= {(1 - K)^2}Var({e_1}) + {K^2}Var({e_2})\\ &=(1 - K{)^2}\sigma _{{e_1}}^2 + {K^2}\sigma _{{e_2}}^2 \end{aligned}
σe^2=Var((1−K)e1+Ke2)=Var((1−K)e1)+Var(Ke2)=(1−K)2Var(e1)+K2Var(e2)=(1−K)2σe12+K2σe22
为了求估计误差方差的最小值,我们令
d
σ
e
^
2
d
K
=
0
\frac{{d\sigma _{\hat e}^2}}{{dK}} = 0
dKdσe^2=0,即:
d
σ
e
^
2
d
K
=
d
[
(
1
−
K
)
2
σ
e
1
2
+
K
2
σ
e
2
2
]
d
K
=
−
2
(
1
−
K
)
σ
e
1
2
+
2
K
σ
e
2
2
=
0
\begin{aligned} \frac{{d\sigma _{\hat e}^2}}{{dK}} &= \frac{{d[{{(1 - K)}^2}\sigma _{{e_1}}^2 + {K^2}\sigma _{{e_2}}^2]}}{{dK}}\\ &= - 2(1 - K)\sigma _{{e_1}}^2 + 2K\sigma _{{e_2}}^2 = 0 \end{aligned}
dKdσe^2=dKd[(1−K)2σe12+K2σe22]=−2(1−K)σe12+2Kσe22=0将
K
K
K提出来得:
K
∗
=
σ
e
1
2
σ
e
1
2
+
σ
e
2
2
{K^*} = \frac{{\sigma _{{e_1}}^2}}{{\sigma _{{e_1}}^2 + \sigma _{{e_2}}^2}}
K∗=σe12+σe22σe12
将
σ
e
1
=
1
{\sigma _{{e_1}}} = 1
σe1=1,
σ
e
2
=
0.5
{\sigma _{{e_2}}} = 0.5
σe2=0.5代入上式得:
K
∗
=
σ
e
1
2
σ
e
1
2
+
σ
e
2
2
=
1
1
+
0.5
2
=
0.8
{K^*} = \frac{{\sigma _{{e_1}}^2}}{{\sigma _{{e_1}}^2 + \sigma _{{e_2}}^2}} = \frac{1}{{1 + {{0.5}^2}}} = 0.8
K∗=σe12+σe22σe12=1+0.521=0.8
σ
e
^
2
\sigma _{\hat e}^2
σe^2对
K
K
K的二阶导数为:
d
2
σ
e
^
2
d
K
2
=
d
(
−
2
(
1
−
K
)
σ
e
1
2
+
2
K
σ
e
2
2
)
d
K
=
2
(
σ
e
1
2
+
σ
e
2
2
)
>
0
\begin{aligned} \frac{{{d^2}\sigma _{\hat e}^2}}{{d{K^2}}} &= \frac{{d( - 2(1 - K)\sigma _{{e_1}}^2 + 2K\sigma _{{e_2}}^2)}}{{dK}}\\ &= 2(\sigma _{{e_1}}^2 + \sigma _{{e_2}}^2) > 0 \end{aligned}
dK2d2σe^2=dKd(−2(1−K)σe12+2Kσe22)=2(σe12+σe22)>0因此当
K
∗
=
σ
e
1
2
σ
e
1
2
+
σ
e
2
2
=
0.8
{K^*} = \frac{{\sigma _{{e_1}}^2}}{{\sigma _{{e_1}}^2 + \sigma _{{e_2}}^2}}= 0.8
K∗=σe12+σe22σe12=0.8时,
σ
e
^
2
\sigma _{\hat e}^2
σe^2为最小值,此时可以得到最有估计值:
Z
^
=
Z
1
+
K
∗
(
Z
2
−
Z
1
)
=
50
+
0.8
×
(
52
−
50
)
=
51.6
\hat Z = {Z_1} + {K^*}({Z_2} - {Z_1}) = 50 + 0.8 \times (52 - 50) = 51.6
Z^=Z1+K∗(Z2−Z1)=50+0.8×(52−50)=51.6
最优估计误差的标准差为:
σ
e
^
=
(
1
−
K
∗
)
2
σ
e
1
2
+
(
K
∗
)
2
σ
e
2
2
≈
0.45
{\sigma _{\hat e}} = \sqrt {{{(1 - {K^*})}^2}\sigma _{{e_1}}^2 + {{({K^*})}^2}\sigma _{{e_2}}^2} \approx 0.45
σe^=(1−K∗)2σe12+(K∗)2σe22≈0.45这一标准差小于每一个传感器单独测量的误差标准差(
σ
e
^
<
σ
e
2
<
σ
e
1
{\sigma _{\hat e}} < {\sigma _{{e_2}}} < {\sigma _{{e_1}}}
σe^<σe2<σe1),数据融合结果如图所示:

1.2.3协方差矩阵
当两个传感器之间是下相互独立的(一个传感器测量的结果不会影响另一个传感器测量的结果),这是在进行数据融合的时候只需要考虑他们各自的方差即可。但是在某种情况下,两个信号之间存在关联(例如一个信号会放大另一个信号),在融合时就需要考虑两者之间的关联。两组信号之间的联动关系使用协方差表示。当有多组信号时,使用协方差矩阵表示。
在统计学中,方差和标准差都是用来度量数据离散程度的量。方差或标准差越大,说明数据离散程度越大。协方差用于衡量两组变量的联合变化程度。协方差用
σ
x
i
x
j
\textcolor{#FF0000}{{\sigma _{{x_i}{x_j}}}}
σxixj表示。
一个三阶的协方差矩阵为:

协方差矩阵是一个方阵,其维度和变量个数相同,其对角线上的元素是单个变量的方差,其余位置是两两不同变量之间的协方差。因为 σ x i x j = σ x j x i \textcolor{#FF0000}{{\sigma _{{x_i}{x_j}}}={\sigma _{{x_j}{x_i}}}} σxixj=σxjxi,所以协方差矩阵是对称阵,即 C ( x 1 , x 2 , x 3 ) = C T ( x 1 , x 2 , x 3 ) \textcolor{#FF0000}{C({x_1},{x_2},{x_3}) = {C^T}({x_1},{x_2},{x_3})} C(x1,x2,x3)=CT(x1,x2,x3)。
对于一组统计数据,协方差矩阵可以简洁明确地给出每个变量之间的联动关系以及变量自身的离散程度。如图中所示:

在卡尔曼滤波器中,我们关心的是随机变量之间的协方差与协方差矩阵。
首先讨论随机变量的协方差,考虑两个随机变量
X
1
{X_1}
X1和
X
2
{X_2}
X2,他们之间的协方差定义为:
σ
X
1
X
2
=
C
o
v
(
X
1
,
X
2
)
=
E
(
(
X
1
−
E
(
X
1
)
)
(
X
2
−
E
(
X
2
)
)
)
=
E
(
X
1
X
2
−
X
1
E
(
X
2
)
−
E
(
X
1
)
X
2
+
E
(
X
1
)
E
(
X
2
)
=
E
(
X
1
X
2
)
−
E
(
X
1
)
E
(
X
2
)
−
E
(
X
1
)
E
(
X
2
)
+
E
(
X
1
)
E
(
X
2
)
=
E
(
X
1
X
2
)
−
E
(
X
1
)
E
(
X
2
)
\begin{aligned} {\textcolor{#FF0000}{\sigma _{{X_1}{X_2}}}} &= C{\rm{ov}}({X_1},{X_2}) = E(({X_1} - E({X_1}))({X_2} - E({X_2})))\\ &= E({X_1}{X_2} - {X_1}E({X_2}) - E({X_1}){X_2} + E({X_1})E({X_2})\\ &= E({X_1}{X_2}) - E({X_1})E({X_2}) - E({X_1})E({X_2}) + E({X_1})E({X_2})\\ &=\textcolor{#FF0000}{ E({X_1}{X_2}) - E({X_1})E({X_2}}) \end{aligned}
σX1X2=Cov(X1,X2)=E((X1−E(X1))(X2−E(X2)))=E(X1X2−X1E(X2)−E(X1)X2+E(X1)E(X2)=E(X1X2)−E(X1)E(X2)−E(X1)E(X2)+E(X1)E(X2)=E(X1X2)−E(X1)E(X2)
特别地,当
X
=
X
1
=
X
2
X = {X_1} = {X_2}
X=X1=X2时,上式变成
C
o
v
(
X
,
X
)
=
E
(
X
2
)
−
E
2
(
X
)
=
V
a
r
(
X
)
C{\rm{ov}}(X,X) = E({X^2}) - {E^2}(X) = Var(X)
Cov(X,X)=E(X2)−E2(X)=Var(X),这说明方差就是一个随机变量与其自身的协方差。另外,如果
X
1
{X_1}
X1和
X
2
{X_2}
X2相互独立,则
E
(
X
1
X
2
)
=
E
(
X
1
)
E
(
X
2
)
E({X_1}{X_2}) = E({X_1})E({X_2})
E(X1X2)=E(X1)E(X2),可得
C
o
v
(
X
1
,
X
2
)
=
0
Cov({X_1},{X_2}) = 0
Cov(X1,X2)=0,即两个相互独立的随机变量之间没有联动关系,协方差为0。
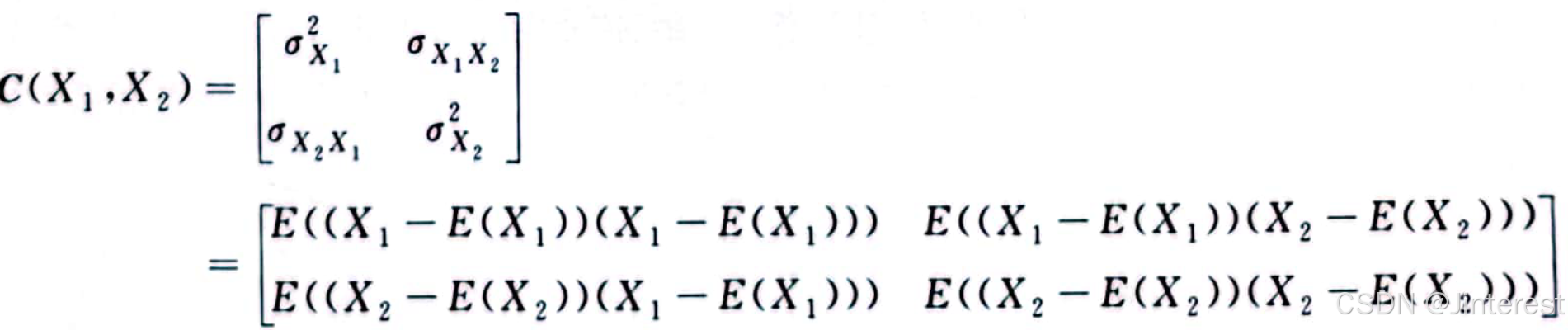
根据矩阵运算法则和期望计算法则可得:
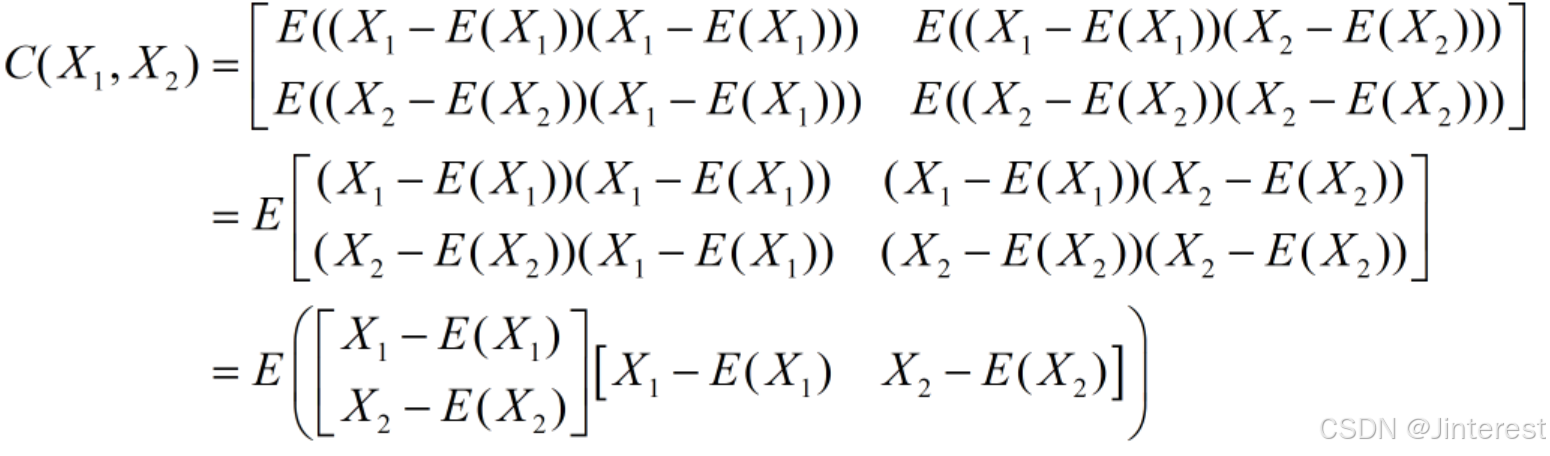
定义一个
2
×
1
2 \times 1
2×1随机向量
X
=
[
X
1
X
2
]
X = \left[ {\begin{matrix} {{X_1}}\\ {{X_2}} \end{matrix}} \right]
X=[X1X2],它的期望
E
(
X
)
=
[
E
(
X
1
)
E
(
X
2
)
]
E(X) = \left[ \begin{array}{l} E({X_1})\\ E({X_2}) \end{array} \right]
E(X)=[E(X1)E(X2)]可得:
[
X
1
−
E
(
X
1
)
X
2
−
E
(
X
2
)
]
=
X
−
E
(
X
)
\left[ {\begin{matrix} {{X_1} - E({X_1})}\\ {{X_2} - E({X_2})} \end{matrix}} \right] = X - E(X)
[X1−E(X1)X2−E(X2)]=X−E(X)则:
C
(
X
1
,
X
2
)
=
E
[
(
X
−
E
(
X
)
)
(
X
−
E
(
X
)
)
T
]
C({X_1},{X_2}) = E\left[ {(X - E(X)){{(X - E(X))}^T}} \right]
C(X1,X2)=E[(X−E(X))(X−E(X))T]将其扩展到一般形式,考虑一个由
n
n
n个随机变量组成的
n
×
1
n\times 1
n×1向量:
X
=
[
X
1
⋮
X
n
]
X = \left[ \begin{array}{l} {X_1}\\ \vdots \\ {X_n} \end{array} \right]
X=
X1⋮Xn
如果向量X中的每一个随机变量
X
i
X_i
Xi都服从正态分布,即
X
i
∼
N
(
μ
X
i
,
σ
X
i
2
)
{X_i} \sim N({\mu _{{X_i}}},\sigma _{{X_i}}^2)
Xi∼N(μXi,σXi2),则定义
X
X
X的期望为:
E
(
X
)
=
[
E
(
X
1
)
⋮
E
(
X
n
)
]
=
[
μ
X
1
⋮
μ
X
n
]
=
μ
X
E(X) = \left[ \begin{array}{l} E({X_1})\\ \vdots \\ E({X_n}) \end{array} \right] = \left[ \begin{array}{l} {\mu _{{X_1}}}\\ \vdots \\ {\mu _{{X_n}}} \end{array} \right] = {\mu _X}
E(X)=
E(X1)⋮E(Xn)
=
μX1⋮μXn
=μX
μ
X
{\mu _X}
μX是一个
n
×
1
n\times 1
n×1向量,则
X
X
X的协方差矩阵为: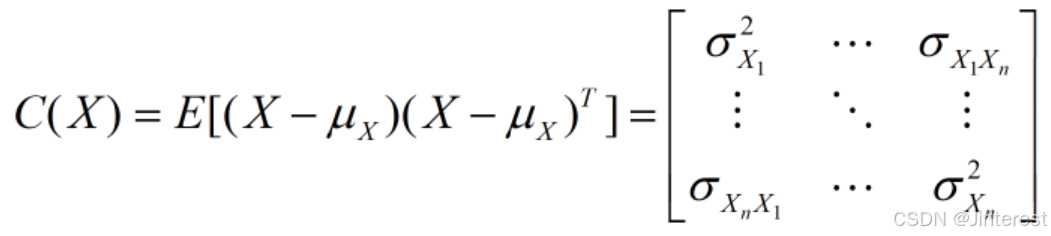
此时,我们可以称这个由随机变量组成的向量
X
X
X服从正态分布
X
∼
N
(
μ
X
,
C
(
X
)
)
X \sim N({\mu _X},C(X))
X∼N(μX,C(X))。特别的,当期望向量
μ
X
=
[
μ
X
1
⋮
μ
X
n
]
=
[
0
⋮
0
]
=
0
{\mu _X} = \left[ \begin{array}{l} {\mu _{{X_1}}}\\ \vdots \\ {\mu _{{X_n}}} \end{array} \right] = \left[ \begin{array}{l} 0\\ \vdots \\ 0 \end{array} \right] = 0
μX=
μX1⋮μXn
=
0⋮0
=0时,
X
X
X服从正态分布
X
∼
N
(
0
,
C
(
X
)
)
X \sim N(0,C(X))
X∼N(0,C(X)),其中协方差矩阵可以写成:
C
(
X
)
=
E
[
X
X
T
]
C(X) = E[X{X^T}]
C(X)=E[XXT]
2.线性卡尔曼滤波器推导
2.1卡尔曼滤波器的研究模型
接下来介绍卡尔曼滤波器的研究对象以及被估计的信号。
























 210
210

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








