hdu1695 bzoj2301(莫比乌斯反演)

hdu1695

题意求：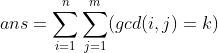

思路：看到gcd求和的式子基本都是莫比乌斯反演。

那么我们对原式除以k，就变成，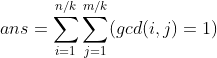

我们设f[k]=(gcd(i,j)=k),F[x]=(k|gcd(i,j)).那么我们求得ans=f[1]。易得F[k]=(n/i)*(m/k)

利用莫比乌斯第二条公式反演得到

 

所以

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod=1e9+7;
const ll maxn=100010;
ll vis[maxn];
ll prime[maxn];
ll cnt;
ll mu[maxn];
ll sum[maxn];
void init()
{
	memset(vis,0,sizeof(vis));
	cnt=0;mu[1]=1;
	for(ll i=2;i<=maxn;i++)
	{
		if(!vis[i]) prime[cnt++]=i,mu[i]=-1;
		for(ll j=0;j<cnt&&prime[j]*i<=maxn;j++)
		{
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				mu[i*prime[j]]=0;break;
			}
			else
			{
				mu[i*prime[j]]=-mu[i];
			}
		}
	}
	sum[0]=0;
	for(ll i=1;i<maxn;i++) sum[i]=sum[i-1]+mu[i];
}

int main()
{
	ll a,b,c,d,k;
	init();
	ll T;scanf("%lld",&T);ll cas=0;
	while(T--)
	{
		cas++;
		scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
		cout<<"Case "<<cas<<": ";
		if(k==0) cout<<0<<endl;
		else
		{
			b/=k;d/=k;
			if(b>d) swap(b,d);
			ll ans1=0;ll last=1;
			for(ll i=1;i<=min(b,d);i=last+1)		//整数分块 
			{
				last=min(b/(b/i),d/(d/i));
				ans1+=(sum[last]-sum[i-1])*(b/i)*(d/i);
			}
			ll ans2=0;
			last=1;
			for(ll i=1;i<=b;i=last+1)				//整数分块 
			{
				last=b/(b/i);
				ans2+=(sum[last]-sum[i-1])*(b/i)*(b/i);
			}
			printf("%lld\n",ans1-ans2/2);			
		}
	}
	return 0;
}

 bzoj2301

题意和上面一题差不多，求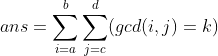，注意这题和上题的区别，区间不再从1开始，并且(x,y)和(y,x)都对答案贡献1。

同上，反演后需要进行容斥。设solve(x,y,k)为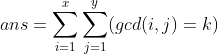

那么答案就是solve(b,d,k)-solve(a-1,d,k)-solve(b,c-1,k)+solve(a-1,c-1,k)

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod=1e9+7;
const ll maxn=100010;
ll vis[maxn];
ll prime[maxn];
ll cnt;
ll mu[maxn];
ll sum[maxn];
void init()
{
	memset(vis,0,sizeof(vis));
	cnt=0;mu[1]=1;
	for(ll i=2;i<=maxn;i++)
	{
		if(!vis[i]) prime[cnt++]=i,mu[i]=-1;
		for(ll j=0;j<cnt&&prime[j]*i<=maxn;j++)
		{
			vis[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				mu[i*prime[j]]=0;break;
			}
			else
			{
				mu[i*prime[j]]=-mu[i];
			}
		}
	}
	sum[0]=0;
	for(ll i=1;i<maxn;i++) sum[i]=sum[i-1]+mu[i];
}
ll solve(ll b, ll d,ll k)
{
	b/=k;d/=k;	
	if(b>d) swap(b,d);
	ll ans1=0;
	ll last=1;
	for(ll i=1;i<=min(b,d);i=last+1)		//整数分块 
	{
		last=min(b/(b/i),d/(d/i));
		ans1+=(sum[last]-sum[i-1])*(b/i)*(d/i);
	}
	ll ans2=0;
	last=1;
	for(ll i=1;i<=b;i=last+1)				//整数分块 
	{
		last=b/(b/i);
		ans2+=(sum[last]-sum[i-1])*(b/i)*(b/i);
	}
	return ans1;	
}
int main()
{
	ll a,b,c,d,k;
	init();
	ll T;scanf("%lld",&T);ll cas=0;
	while(T--)
	{
		cas++;
		scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&k);
		if(k==0) cout<<0<<endl;
		else
		{
			ll ans=solve(b,d,k)-solve(a-1,d,k)-solve(b,c-1,k)+solve(a-1,c-1,k);
			printf("%lld\n",ans);
		}
	}
	return 0;
}